probplot#
- scipy.stats.probplot(x, sparams=(), dist='norm', fit=True, plot=None, rvalue=False)[Quelle]#
Berechnet Quantile für ein Wahrscheinlichkeitsdiagramm und zeigt optional die Grafik an.
Erzeugt ein Wahrscheinlichkeitsdiagramm von Stichprobendaten gegen die Quantile einer spezifizierten theoretischen Verteilung (standardmäßig die Normalverteilung).
probplotberechnet optional eine beste Anpassungslinie für die Daten und plottet die Ergebnisse mithilfe von Matplotlib oder einer gegebenen Plot-Funktion.- Parameter:
- xarray_like
Stichproben-/Antwortdaten, aus denen
probplotdie Grafik erstellt.- sparamstuple, optional
Verteilungsspezifische Formparameter (Formparameter plus Lage und Skalierung).
- diststr oder stats.distributions-Instanz, optional
Verteilung oder Name der Verteilungsfunktion. Standard ist „norm“ für ein Wahrscheinlichkeitsdiagramm der Normalverteilung. Objekte, die genug wie eine Instanz von stats.distributions aussehen (d. h. sie haben eine
ppf-Methode), werden ebenfalls akzeptiert.- fitbool, optional
Passt eine Methode der kleinsten Quadrate (beste Anpassung) an die Stichprobendaten an, wenn True (Standard).
- plotObjekt, optional
Wenn angegeben, werden die Quantile geplottet. Wenn angegeben und
fitTrue ist, wird auch die Methode der kleinsten Quadrate geplottet. plot ist ein Objekt, das die Methoden „plot“ und „text“ haben muss. Das Modulmatplotlib.pyplotoder ein Matplotlib-Achsenobjekt kann verwendet werden, oder ein benutzerdefiniertes Objekt mit denselben Methoden. Standard ist None, was bedeutet, dass keine Grafik erstellt wird.- rvaluebool, optional
Wenn plot angegeben ist und
fitTrue ist, wird durch Setzen von rvalue auf True der Bestimmtheitskoeffizient in der Grafik angezeigt. Standard ist False.
- Rückgabe:
- (osm, osr)tuple von ndarrays
Tupel von theoretischen Quantilen (osm, oder Medianen der Ordnungsstatistiken) und geordneten Antworten (osr). osr ist einfach sortiertes Eingabe-x. Details zur Berechnung von osm finden Sie im Abschnitt Hinweise.
- (slope, intercept, r)tuple von floats, optional
Tupel, das das Ergebnis der Methode der kleinsten Quadrate enthält, wenn dieses von
probplotdurchgeführt wird. r ist die Quadratwurzel des Bestimmtheitskoeffizienten. Wennfit=Falseundplot=None, wird dieses Tupel nicht zurückgegeben.
Hinweise
Auch wenn plot angegeben ist, wird die Grafik nicht von
probplotangezeigt oder gespeichert.plt.show()oderplt.savefig('figname.png')sollten nach dem Aufruf vonprobplotverwendet werden.probplotgeneriert ein Wahrscheinlichkeitsdiagramm, das nicht mit einem Q-Q- oder P-P-Diagramm verwechselt werden sollte. Statsmodels bietet umfangreichere Funktionalitäten dieser Art, siehestatsmodels.api.ProbPlot.Die für die theoretischen Quantile (Horizontale Achse des Wahrscheinlichkeitsdiagramms) verwendete Formel ist Fillibens Schätzung
quantiles = dist.ppf(val), for 0.5**(1/n), for i = n val = (i - 0.3175) / (n + 0.365), for i = 2, ..., n-1 1 - 0.5**(1/n), for i = 1
wobei
iden i-ten geordneten Wert angibt undndie Gesamtzahl der Werte ist.Beispiele
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt >>> nsample = 100 >>> rng = np.random.default_rng()
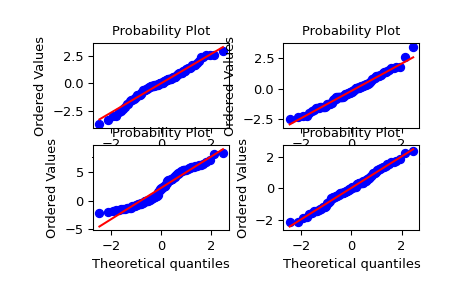
Eine t-Verteilung mit wenigen Freiheitsgraden
>>> ax1 = plt.subplot(221) >>> x = stats.t.rvs(3, size=nsample, random_state=rng) >>> res = stats.probplot(x, plot=plt)
Eine t-Verteilung mit vielen Freiheitsgraden
>>> ax2 = plt.subplot(222) >>> x = stats.t.rvs(25, size=nsample, random_state=rng) >>> res = stats.probplot(x, plot=plt)
Eine Mischung aus zwei Normalverteilungen mit Broadcasting
>>> ax3 = plt.subplot(223) >>> x = stats.norm.rvs(loc=[0,5], scale=[1,1.5], ... size=(nsample//2,2), random_state=rng).ravel() >>> res = stats.probplot(x, plot=plt)
Eine Standardnormalverteilung
>>> ax4 = plt.subplot(224) >>> x = stats.norm.rvs(loc=0, scale=1, size=nsample, random_state=rng) >>> res = stats.probplot(x, plot=plt)
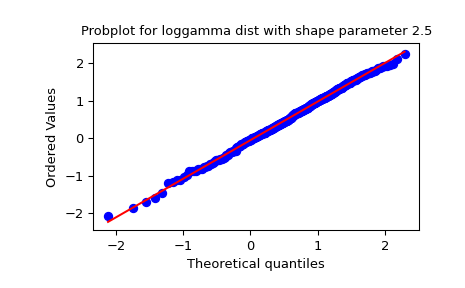
Erzeugt eine neue Grafik mit einer Log-Gamma-Verteilung unter Verwendung der Schlüsselwörter
distundsparams>>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> x = stats.loggamma.rvs(c=2.5, size=500, random_state=rng) >>> res = stats.probplot(x, dist=stats.loggamma, sparams=(2.5,), plot=ax) >>> ax.set_title("Probplot for loggamma dist with shape parameter 2.5")
Zeigt die Ergebnisse mit Matplotlib an
>>> plt.show()