scipy.stats.

fit

scipy.stats.fit(dist, data, bounds=None, *, guess=None, method='mle', optimizer=<function differential_evolution>)

Eine diskrete oder kontinuierliche Verteilung an Daten anpassen

Gegeben eine Verteilung, Daten und Grenzen für die Parameter der Verteilung, gib Schätzungen der maximalen Likelihood der Parameter zurück.

Parameter:

distscipy.stats.rv_continuous oder scipy.stats.rv_discrete

Das Objekt, das die an die Daten anzupassende Verteilung repräsentiert.

data1D array_like

Die Daten, an die die Verteilung angepasst werden soll. Wenn die Daten np.nan, np.inf oder -np.inf enthalten, löst die Fit-Methode einen ValueError aus.

boundsdict oder Sequenz von Tupeln, optional

Wenn es sich um ein Wörterbuch handelt, ist jeder Schlüssel der Name eines Parameters der Verteilung, und der entsprechende Wert ist ein Tupel, das die untere und obere Grenze für diesen Parameter enthält. Wenn die Verteilung nur für einen endlichen Wertebereich dieses Parameters definiert ist, ist kein Eintrag für diesen Parameter erforderlich; z. B. haben einige Verteilungen Parameter, die im Intervall [0, 1] liegen müssen. Grenzen für die Parameter Ort (loc) und Skala (scale) sind optional; standardmäßig sind sie auf 0 bzw. 1 festgelegt.

Wenn es sich um eine Sequenz handelt, ist das Element *i* ein Tupel, das die untere und obere Grenze für den *i*-ten Parameter der Verteilung enthält. In diesem Fall müssen Grenzen für *alle* Verteilungsparameter angegeben werden. Optional können Grenzen für Ort und Skala den Verteilungsparametern folgen.

Wenn eine Form fixiert werden soll (z. B. wenn sie bekannt ist), können die untere und obere Grenze gleich sein. Wenn eine vom Benutzer bereitgestellte untere oder obere Grenze außerhalb einer Grenze des Definitionsbereichs der Verteilung liegt, ersetzt die Grenze des Verteilungsbereichs den vom Benutzer bereitgestellten Wert. Ebenso werden Parameter, die ganzzahlig sein müssen, auf ganzzahlige Werte innerhalb der vom Benutzer bereitgestellten Grenzen beschränkt.

guessdict oder array_like, optional

Wenn es sich um ein Wörterbuch handelt, ist jeder Schlüssel der Name eines Parameters der Verteilung, und der entsprechende Wert ist eine Schätzung für den Wert des Parameters.

Wenn es sich um eine Sequenz handelt, ist das Element *i* eine Schätzung für den *i*-ten Parameter der Verteilung. In diesem Fall müssen Schätzungen für *alle* Verteilungsparameter angegeben werden.

Wenn guess nicht angegeben ist, werden keine Schätzungen für die Entscheidungsvariablen an den Optimierer übergeben. Wenn guess angegeben ist, werden Schätzungen für fehlende Parameter auf den Mittelwert der unteren und oberen Grenzen gesetzt. Schätzungen für ganzzahlige Parameter werden auf ganzzahlige Werte gerundet, und Schätzungen, die außerhalb der Schnittmenge der vom Benutzer angegebenen Grenzen und des Definitionsbereichs der Verteilung liegen, werden beschnitten.

method{‘mle’, ‘mse’}

Mit method="mle" (Standard) wird die Anpassung durch Minimierung der negativen Log-Likelihood-Funktion berechnet. Für Beobachtungen außerhalb des Trägers der Verteilung wird eine große, endliche Strafe (anstelle einer unendlichen negativen Log-Likelihood) angewendet. Mit method="mse" wird die Anpassung durch Minimierung der negativen Log-Produkt-Abstandsfunktion berechnet. Die gleiche Strafe wird für Beobachtungen außerhalb des Trägers angewendet. Wir folgen dem Ansatz von [1], der für Stichproben mit wiederholten Beobachtungen verallgemeinert wird.

optimizeraufrufbar, optional

optimizer ist eine aufrufbare Funktion, die das folgende Positionsargument akzeptiert.

funcallable

Die zu optimierende Zielfunktion. fun akzeptiert ein Argument x, kandidatenförmige Parameter der Verteilung, und gibt den Wert der Zielfunktion gegeben x, dist und die bereitgestellten data zurück. Die Aufgabe von optimizer ist es, Werte der Entscheidungsvariablen zu finden, die fun minimieren.

optimizer muss auch das folgende Schlüsselwortargument akzeptieren.

boundsSequenz von Tupeln

Die Grenzen für die Werte der Entscheidungsvariablen; jedes Element ist ein Tupel, das die untere und obere Grenze für eine Entscheidungsvariable enthält.

Wenn guess angegeben ist, muss optimizer auch das folgende Schlüsselwortargument akzeptieren.

x0array_like

Die Schätzungen für jede Entscheidungsvariable.

Wenn die Verteilung irgendwelche Formparameter hat, die ganzzahlig sein müssen, oder wenn die Verteilung diskret ist und der Ortsparameter nicht fixiert ist, muss optimizer auch das folgende Schlüsselwortargument akzeptieren.

integralityarray_like von bools

Für jede Entscheidungsvariable True, wenn die Entscheidungsvariable auf ganzzahlige Werte beschränkt sein muss, und False, wenn die Entscheidungsvariable kontinuierlich ist.

optimizer muss ein Objekt zurückgeben, z. B. eine Instanz von scipy.optimize.OptimizeResult, das die optimalen Werte der Entscheidungsvariablen im Attribut x enthält. Wenn die Attribute fun, status oder message bereitgestellt werden, werden sie in das von fit zurückgegebene Ergebnisobjekt aufgenommen.

Rückgabe:

resultFitResult

Ein Objekt mit den folgenden Feldern.

paramsnamedtuple

Ein namedtuple, das die maximalen Likelihood-Schätzungen der Formparameter, des Orts und (falls zutreffend) der Skala der Verteilung enthält.

successbool oder None

Ob der Optimierer die Optimierung als erfolgreich beendet betrachtete oder nicht.

messagestr oder None

Jede Statusmeldung, die vom Optimierer bereitgestellt wurde.

Das Objekt hat die folgende Methode

nllf(params=None, data=None)

Standardmäßig die negative Log-Likelihood-Funktion an den angepassten params für die gegebenen data. Akzeptiert ein Tupel, das alternative Formen, Ort und Skala der Verteilung sowie ein Array von alternativen Daten enthält.

plot(ax=None)

Überlagert die Dichtefunktion/Wahrscheinlichkeitsmassenfunktion der angepassten Verteilung über einem normalisierten Histogramm der Daten.

Siehe auch

rv_continuous, rv_discrete

Hinweise

Die Wahrscheinlichkeit, dass die Optimierung zu einer Schätzung der maximalen Likelihood konvergiert, ist höher, wenn der Benutzer enge Grenzen angibt, die die Schätzung der maximalen Likelihood enthalten. Wenn beispielsweise eine Binomialverteilung an Daten angepasst wird, kann die Anzahl der Experimente, denen jeder Stichprobenwert zugrunde liegt, bekannt sein, in welchem Fall der entsprechende Formparameter n fixiert werden kann.

Referenzen

[1]

Shao, Yongzhao und Marjorie G. Hahn. „Maximum product of spacings method: a unified formulation with illustration of strong consistency.“ Illinois Journal of Mathematics 43.3 (1999): 489-499.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Angenommen, wir möchten eine Verteilung an die folgenden Daten anpassen.

>>> import numpy as np
>>> from scipy import stats
>>> rng = np.random.default_rng()
>>> dist = stats.nbinom
>>> shapes = (5, 0.5)
>>> data = dist.rvs(*shapes, size=1000, random_state=rng)

Angenommen, wir wissen nicht, wie die Daten generiert wurden, aber wir vermuten, dass sie einer negativen Binomialverteilung mit den Parametern *n* und *p* folgen. (Siehe scipy.stats.nbinom.) Wir glauben, dass der Parameter *n* kleiner als 30 war, und wir wissen, dass der Parameter *p* im Intervall [0, 1] liegen muss. Wir zeichnen diese Informationen in einer Variablen bounds auf und übergeben diese Informationen an fit.

>>> bounds = [(0, 30), (0, 1)]
>>> res = stats.fit(dist, data, bounds)

fit sucht innerhalb der vom Benutzer angegebenen bounds nach den Werten, die am besten zu den Daten passen (im Sinne der maximalen Likelihood-Schätzung). In diesem Fall fand es Formen, die denen ähneln, mit denen die Daten tatsächlich generiert wurden.

>>> res.params
FitParams(n=5.0, p=0.5028157644634368, loc=0.0)  # may vary

Wir können die Ergebnisse visualisieren, indem wir die Wahrscheinlichkeitsmassenfunktion der Verteilung (mit den an die Daten angepassten Formen) über einem normalisierten Histogramm der Daten überlagern.

>>> import matplotlib.pyplot as plt  # matplotlib must be installed to plot
>>> res.plot()
>>> plt.show()

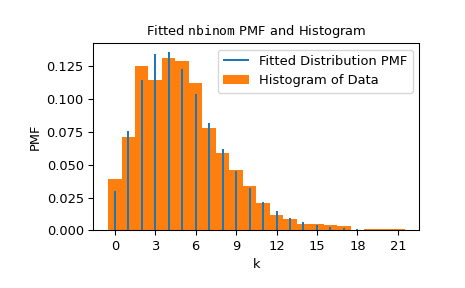
Beachten Sie, dass die Schätzung für *n* exakt ganzzahlig war; dies liegt daran, dass der Definitionsbereich der nbinom PMF nur ganzzahlige *n* enthält, und das nbinom-Objekt weiß dies. nbinom weiß auch, dass die Form *p* ein Wert zwischen 0 und 1 sein muss. In solchen Fällen – wenn der Definitionsbereich der Verteilung in Bezug auf einen Parameter endlich ist – müssen wir keine Grenzen für den Parameter angeben.

>>> bounds = {'n': (0, 30)}  # omit parameter p using a `dict`
>>> res2 = stats.fit(dist, data, bounds)
>>> res2.params
FitParams(n=5.0, p=0.5016492009232932, loc=0.0)  # may vary

Wenn wir erzwingen möchten, dass die Verteilung mit fixiertem *n* gleich 6 angepasst wird, können wir sowohl die untere als auch die obere Grenze für *n* auf 6 setzen. Beachten Sie jedoch, dass der Wert der zu optimierenden Zielfunktion in diesem Fall typischerweise schlechter (höher) ist.

>>> bounds = {'n': (6, 6)}  # fix parameter `n`
>>> res3 = stats.fit(dist, data, bounds)
>>> res3.params
FitParams(n=6.0, p=0.5486556076755706, loc=0.0)  # may vary
>>> res3.nllf() > res.nllf()
True  # may vary

Beachten Sie, dass die numerischen Ergebnisse der vorherigen Beispiele typisch sind, aber sie können variieren, da der Standardoptimierer, der von fit verwendet wird, scipy.optimize.differential_evolution, stochastisch ist. Wir können jedoch die vom Optimierer verwendeten Einstellungen anpassen, um die Reproduzierbarkeit sicherzustellen – oder sogar einen anderen Optimierer zu verwenden – mithilfe des Parameters optimizer.

>>> from scipy.optimize import differential_evolution
>>> rng = np.random.default_rng()
>>> def optimizer(fun, bounds, *, integrality):
...     return differential_evolution(fun, bounds, strategy='best2bin',
...                                   rng=rng, integrality=integrality)
>>> bounds = [(0, 30), (0, 1)]
>>> res4 = stats.fit(dist, data, bounds, optimizer=optimizer)
>>> res4.params
FitParams(n=5.0, p=0.5015183149259951, loc=0.0)

ZurückIn Tab öffnen