scipy.stats.nhypergeom

scipy.stats.nhypergeom = <scipy.stats._discrete_distns.nhypergeom_gen Objekt>

Eine negative hypergeometrische diskrete Zufallsvariable.

Betrachten Sie eine Box mit \(M\) Kugeln: \(n\) rote und \(M-n\) blaue. Wir ziehen zufällig Kugeln aus der Box, eine nach der anderen und *ohne* Zurücklegen, bis wir \(r\) blaue Kugeln gezogen haben. nhypergeom ist die Verteilung der Anzahl roter Kugeln \(k\), die wir gezogen haben.

Als Instanz der Klasse rv_discrete erbt nhypergeom von ihr eine Sammlung allgemeiner Methoden (siehe unten für die vollständige Liste) und vervollständigt diese mit Details, die spezifisch für diese spezielle Verteilung sind.

Methoden

rvs(M, n, r, loc=0, size=1, random_state=None)	Zufallsvariaten.
pmf(k, M, n, r, loc=0)	Wahrscheinlichkeitsmassenfunktion.
logpmf(k, M, n, r, loc=0)	Logarithmus der Wahrscheinlichkeitsmassenfunktion.
cdf(k, M, n, r, loc=0)	Kumulative Verteilungsfunktion.
logcdf(k, M, n, r, loc=0)	Logarithmus der kumulativen Verteilungsfunktion.
sf(k, M, n, r, loc=0)	Überlebensfunktion (auch definiert als 1 - cdf, aber sf ist manchmal genauer).
logsf(k, M, n, r, loc=0)	Logarithmus der Überlebensfunktion.
ppf(q, M, n, r, loc=0)	Perzentilpunktfunktion (Umkehrung von cdf — Perzentile).
isf(q, M, n, r, loc=0)	Umgekehrte Überlebensfunktion (Umkehrung von sf).
stats(M, n, r, loc=0, moments=’mv’)	Mittelwert(‚m‘), Varianz(‚v‘), Schiefe(‚s‘) und/oder Kurtosis(‚k‘).
entropy(M, n, r, loc=0)	(Differential-)Entropie der RV.
expect(func, args=(M, n, r), loc=0, lb=None, ub=None, conditional=False)	Erwartungswert einer Funktion (einer Variablen) bezüglich der Verteilung.
median(M, n, r, loc=0)	Median der Verteilung.
mean(M, n, r, loc=0)	Mittelwert der Verteilung.
var(M, n, r, loc=0)	Varianz der Verteilung.
std(M, n, r, loc=0)	Standardabweichung der Verteilung.
interval(confidence, M, n, r, loc=0)	Konfidenzintervall mit gleichen Flächen um den Median.

Siehe auch

hypergeom, binom, nbinom

Hinweise

Die Symbole, die zur Bezeichnung der Formparameter (M, n und r) verwendet werden, sind nicht universell akzeptiert. Siehe die Beispiele zur Klärung der hier verwendeten Definitionen.

Die Wahrscheinlichkeitsmassenfunktion ist definiert als,

\[f(k; M, n, r) = \frac{{{k+r-1}\choose{k}}{{M-r-k}\choose{n-k}}} {{M \choose n}}\]

für \(k \in [0, n]\), \(n \in [0, M]\), \(r \in [0, M-n]\), und der Binomialkoeffizient ist

\[\binom{n}{k} \equiv \frac{n!}{k! (n - k)!}.\]

Dies entspricht der Beobachtung von \(k\) Erfolgen in \(k+r-1\) Stichproben, wobei die \(k+r\)-te Stichprobe ein Misserfolg ist. Das erstere kann als hypergeometrische Verteilung modelliert werden. Die Wahrscheinlichkeit des letzteren ist einfach die Anzahl der verbleibenden Misserfolge \(M-n-(r-1)\) geteilt durch die Größe der verbleibenden Population \(M-(k+r-1)\). Diese Beziehung kann wie folgt gezeigt werden:

\[NHG(k;M,n,r) = HG(k;M,n,k+r-1)\frac{(M-n-(r-1))}{(M-(k+r-1))}\]

wobei \(NHG\) die Wahrscheinlichkeitsmassenfunktion (PMF) der negativen hypergeometrischen Verteilung und \(HG\) die PMF der hypergeometrischen Verteilung ist.

Die obige Wahrscheinlichkeitsmassenfunktion ist in der "standardisierten" Form definiert. Um die Verteilung zu verschieben, verwenden Sie den Parameter loc. Insbesondere ist nhypergeom.pmf(k, M, n, r, loc) identisch mit nhypergeom.pmf(k - loc, M, n, r).

Referenzen

[1]

Negative Hypergeometrische Verteilung auf Wikipedia https://en.wikipedia.org/wiki/Negative_hypergeometric_distribution

[2]

Negative Hypergeometrische Verteilung von http://www.math.wm.edu/~leemis/chart/UDR/PDFs/Negativehypergeometric.pdf

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy.stats import nhypergeom
>>> import matplotlib.pyplot as plt

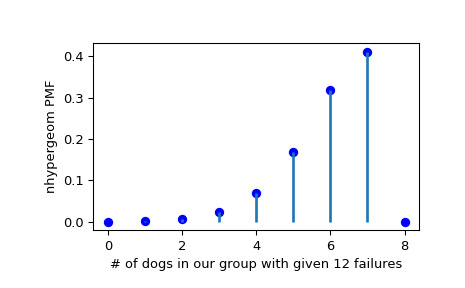
Angenommen, wir haben eine Sammlung von 20 Tieren, von denen 7 Hunde sind. Wenn wir dann die Wahrscheinlichkeit wissen wollen, eine bestimmte Anzahl von Hunden (Erfolgen) in einer Stichprobe mit genau 12 Tieren zu finden, die keine Hunde sind (Misserfolge), können wir eine eingefrorene Verteilung initialisieren und die Wahrscheinlichkeitsmassenfunktion plotten.

>>> M, n, r = [20, 7, 12]
>>> rv = nhypergeom(M, n, r)
>>> x = np.arange(0, n+2)
>>> pmf_dogs = rv.pmf(x)

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, pmf_dogs, 'bo')
>>> ax.vlines(x, 0, pmf_dogs, lw=2)
>>> ax.set_xlabel('# of dogs in our group with given 12 failures')
>>> ax.set_ylabel('nhypergeom PMF')
>>> plt.show()

Anstatt eine eingefrorene Verteilung zu verwenden, können wir auch direkt die Methoden von nhypergeom verwenden. Um beispielsweise die Wahrscheinlichkeitsmassenfunktion zu erhalten, verwenden Sie:

>>> prb = nhypergeom.pmf(x, M, n, r)

Und um Zufallszahlen zu generieren:

>>> R = nhypergeom.rvs(M, n, r, size=10)

Um die Beziehung zwischen hypergeom und nhypergeom zu überprüfen, verwenden Sie:

>>> from scipy.stats import hypergeom, nhypergeom
>>> M, n, r = 45, 13, 8
>>> k = 6
>>> nhypergeom.pmf(k, M, n, r)
0.06180776620271643
>>> hypergeom.pmf(k, M, n, k+r-1) * (M - n - (r-1)) / (M - (k+r-1))
0.06180776620271644

ZurückIn Tab öffnen