scipy.stats.

ppcc_plot

scipy.stats.ppcc_plot(x, a, b, dist='tukeylambda', plot=None, N=80)

Berechnet und plottet optional den Wahrscheinlichkeitsplot-Korrelationskoeffizienten.

Das Wahrscheinlichkeitsplot-Korrelationskoeffizienten (PPCC)-Diagramm kann verwendet werden, um den optimalen Formparameter für eine einparametrige Verteilungsfamilie zu bestimmen. Es kann nicht für Verteilungen ohne Formparameter (wie die Normalverteilung) oder mit mehreren Formparametern verwendet werden.

Standardmäßig wird eine Tukey-Lambda-Verteilung (stats.tukeylambda) verwendet. Ein Tukey-Lambda PPCC-Diagramm interpoliert von Verteilungen mit langen Schwänzen zu Verteilungen mit kurzen Schwänzen über eine ungefähr normale, und ist daher in der Praxis besonders nützlich.

Parameter:

xarray_like

Eingabearray.

a, bSkalar

Untere und obere Grenzen des zu verwendenden Formparameters.

diststr oder stats.distributions-Instanz, optional

Name der Verteilung oder Verteilungsfunktion. Objekte, die stark wie eine Instanz von stats.distributions aussehen (d. h. sie haben eine ppf-Methode), werden ebenfalls akzeptiert. Der Standardwert ist 'tukeylambda'.

plotObjekt, optional

Wenn angegeben, werden die PPCC gegen den Formparameter geplottet. plot ist ein Objekt, das die Methoden "plot" und "text" haben muss. Das Modul matplotlib.pyplot oder ein Matplotlib Axes-Objekt kann verwendet werden, oder ein benutzerdefiniertes Objekt mit denselben Methoden. Der Standardwert ist None, was bedeutet, dass kein Plot erstellt wird.

Nint, optional

Anzahl der Punkte auf der horizontalen Achse (gleichmäßig verteilt von a bis b).

Rückgabe:

svalsndarray

Die Formwerte, für die ppcc berechnet wurde.

ppccndarray

Die berechneten Wahrscheinlichkeitsplot-Korrelationskoeffizientenwerte.

Siehe auch

ppcc_max, probplot, boxcox_normplot, tukeylambda

Referenzen

J.J. Filliben, „The Probability Plot Correlation Coefficient Test for Normality“, Technometrics, Vol. 17, S. 111–117, 1975.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Zuerst generieren wir einige Zufallsdaten aus einer Weibull-Verteilung mit dem Formparameter 2,5 und plotten das Histogramm der Daten.

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> c = 2.5
>>> x = stats.weibull_min.rvs(c, scale=4, size=2000, random_state=rng)

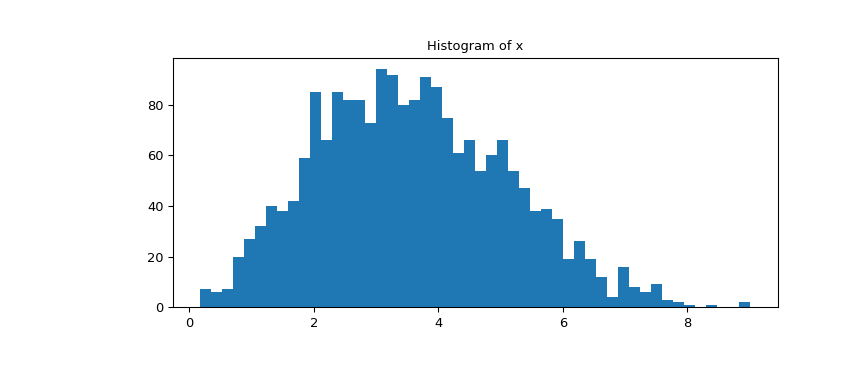
Betrachten Sie das Histogramm der Daten.

>>> fig1, ax = plt.subplots(figsize=(9, 4))
>>> ax.hist(x, bins=50)
>>> ax.set_title('Histogram of x')
>>> plt.show()

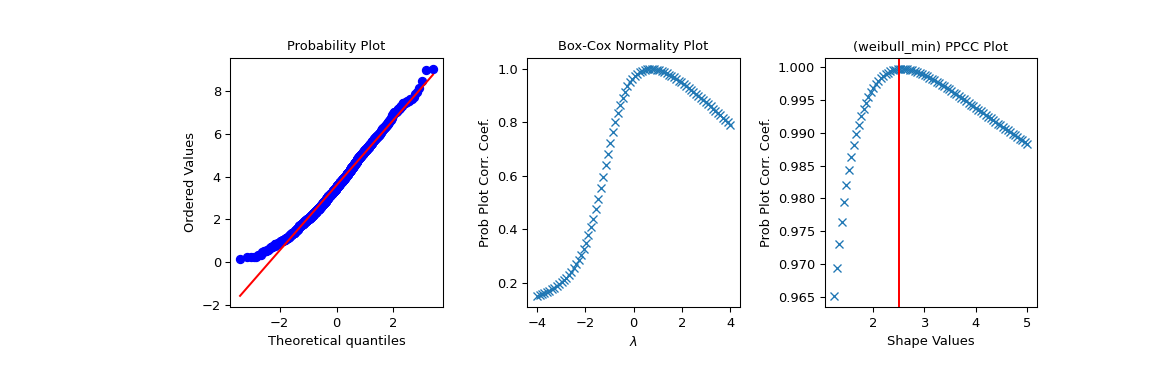
Nun untersuchen wir diese Daten mit einem PPCC-Diagramm sowie dem zugehörigen Wahrscheinlichkeitsdiagramm und dem Box-Cox-Normdiagramm. Eine rote Linie wird dort gezogen, wo wir den maximalen PPCC-Wert erwarten (beim Formparameter c, der oben verwendet wurde).

>>> fig2 = plt.figure(figsize=(12, 4))
>>> ax1 = fig2.add_subplot(1, 3, 1)
>>> ax2 = fig2.add_subplot(1, 3, 2)
>>> ax3 = fig2.add_subplot(1, 3, 3)
>>> res = stats.probplot(x, plot=ax1)
>>> res = stats.boxcox_normplot(x, -4, 4, plot=ax2)
>>> res = stats.ppcc_plot(x, c/2, 2*c, dist='weibull_min', plot=ax3)
>>> ax3.axvline(c, color='r')
>>> plt.show()

ZurückIn Tab öffnen