scipy.stats.

siegelslopes#

scipy.stats.siegelslopes(y, x=None, method='hierarchical', *, axis=None, nan_policy='propagate', keepdims=False)[Quelle]#

Berechnet den Siegel-Schätzer für eine Punktmenge (x, y).

siegelslopes implementiert eine Methode für robuste lineare Regression unter Verwendung wiederholter Mediane (siehe [1]), um eine Linie an die Punkte (x, y) anzupassen. Die Methode ist robust gegenüber Ausreißern mit einem asymptotischen Breakpoint von 50 %.

Parameter:

yarray_like

Abhängige Variable.

xarray_like oder None, optional

Unabhängige Variable. Wenn None, wird stattdessen arange(len(y)) verwendet.

method{‘hierarchical’, ‘separate’}

Wenn ‘hierarchical’, schätzen Sie den Achsenabschnitt mit der geschätzten Steigung slope (Standardoption). Wenn ‘separate’, schätzen Sie den Achsenabschnitt unabhängig von der geschätzten Steigung. Siehe Hinweise für Details.

axisint oder None, Standard: None

Wenn es sich um eine ganze Zahl handelt, ist dies die Achse des Eingabearrays, entlang der die Statistik berechnet wird. Die Statistik jedes Achsen-Slices (z. B. Zeile) der Eingabe erscheint dann in einem entsprechenden Element der Ausgabe. Wenn None, wird die Eingabe vor der Berechnung der Statistik geglättet.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Definiert, wie Eingabe-NaNs behandelt werden.

propagate: Wenn ein NaN in der Achsen-Slice (z. B. Zeile) vorhanden ist, entlang der die Statistik berechnet wird, wird der entsprechende Eintrag der Ausgabe NaN sein.
omit: NaNs werden bei der Berechnung weggelassen. Wenn im Achsen-Slice, entlang dem die Statistik berechnet wird, nicht genügend Daten verbleiben, wird der entsprechende Eintrag der Ausgabe NaN sein.
raise: Wenn ein NaN vorhanden ist, wird ein ValueError ausgelöst.

keepdimsbool, Standard: False

Wenn dies auf True gesetzt ist, bleiben die reduzierten Achsen im Ergebnis als Dimensionen mit der Größe eins erhalten. Mit dieser Option wird das Ergebnis korrekt gegen das Eingabearray gestreut (broadcasted).

Rückgabe:

resultSiegelslopesResult Instanz

Der Rückgabewert ist ein Objekt mit folgenden Attributen:

slopefloat: Schätzung der Steigung der Regressionslinie.
interceptfloat: Schätzung des Achsenabschnitts der Regressionslinie.

Siehe auch

theilslopes: eine ähnliche Technik ohne wiederholte Mediane

Hinweise

Mit n = len(y), berechnen Sie m_j als den Median der Steigungen vom Punkt (x[j], y[j]) zu allen anderen n-1 Punkten. slope ist dann der Median aller Steigungen m_j. Zwei Wege zur Schätzung des Achsenabschnitts werden in [1] angegeben, die über den Parameter method gewählt werden können. Der hierarchische Ansatz verwendet die geschätzte Steigung slope und berechnet intercept als den Median von y - slope*x. Der andere Ansatz schätzt den Achsenabschnitt separat wie folgt: für jeden Punkt (x[j], y[j]), berechnen Sie die Achsenabschnitte aller n-1 Linien durch die verbleibenden Punkte und nehmen den Median i_j. intercept ist der Median der i_j.

Die Implementierung berechnet n mal den Median eines Vektors der Größe n, was für große Vektoren langsam sein kann. Es gibt effizientere Algorithmen (siehe [2]), die hier nicht implementiert sind.

Aus Kompatibilitätsgründen mit älteren Versionen von SciPy verhält sich der Rückgabewert wie ein namedtuple der Länge 2 mit den Feldern slope und intercept, sodass man weiterhin schreiben kann

slope, intercept = siegelslopes(y, x)

Seit SciPy 1.9 werden np.matrix-Eingaben (für neuen Code nicht empfohlen) vor der Berechnung in np.ndarray konvertiert. In diesem Fall ist die Ausgabe eine Skalar- oder np.ndarray mit geeigneter Form anstelle eines 2D-np.matrix. Ebenso werden, während maskierte Elemente von Masked Arrays ignoriert werden, die Ausgabe eine Skalar- oder np.ndarray anstelle eines Masked Arrays mit mask=False sein.

Referenzen

[1] (1,2)

A. Siegel, „Robust Regression Using Repeated Medians“, Biometrika, Bd. 69, S. 242-244, 1982.

[2]

A. Stein und M. Werman, „Finding the repeated median regression line“, Proceedings of the Third Annual ACM-SIAM Symposium on Discrete Algorithms, S. 409-413, 1992.

Beispiele

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-5, 5, num=150)
>>> y = x + np.random.normal(size=x.size)
>>> y[11:15] += 10  # add outliers
>>> y[-5:] -= 7

Berechnen Sie die Steigung und den Achsenabschnitt. Zum Vergleich wird auch die Kleinste-Quadrate-Anpassung mit linregress berechnet

>>> res = stats.siegelslopes(y, x)
>>> lsq_res = stats.linregress(x, y)

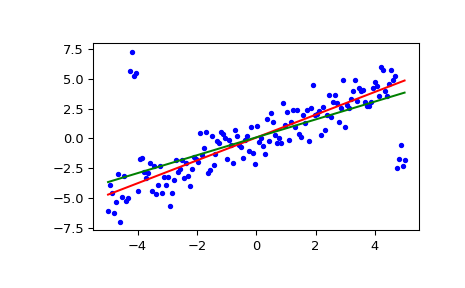
Plotten Sie die Ergebnisse. Die Siegel-Regressionslinie ist rot dargestellt. Die grüne Linie zeigt zum Vergleich die Kleinste-Quadrate-Anpassung.

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, y, 'b.')
>>> ax.plot(x, res[1] + res[0] * x, 'r-')
>>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-')
>>> plt.show()

../../_images/scipy-stats-siegelslopes-1.png