theilslopes#
- scipy.stats.theilslopes(y, x=None, alpha=0.95, method='separate', *, axis=None, nan_policy='propagate', keepdims=False)[Quelle]#
Berechnet den Theil-Sen-Schätzer für eine Menge von Punkten (x, y).
theilslopesimplementiert eine Methode zur robusten linearen Regression. Sie berechnet die Steigung als Median aller Steigungen zwischen gepaarten Werten.- Parameter:
- yarray_like
Abhängige Variable.
- xarray_like oder None, optional
Unabhängige Variable. Wenn None, wird stattdessen
arange(len(y))verwendet.- alphafloat, optional
Konfidenzgrad zwischen 0 und 1. Standard ist eine 95%ige Konfidenz. Beachten Sie, dass
alphasymmetrisch um 0,5 ist, d. h. sowohl 0,1 als auch 0,9 werden als „ermittle das 90%ige Konfidenzintervall“ interpretiert.- method{‘joint’, ‘separate’}, optional
Methode zur Berechnung der Schätzung für den Achsenabschnitt. Folgende Methoden werden unterstützt:
‘joint’: Verwendet np.median(y - slope * x) als Achsenabschnitt.
- ‘separate’: Verwendet np.median(y) - slope * np.median(x)
als Achsenabschnitt.
Standard ist ‘separate’.
Hinzugefügt in Version 1.8.0.
- axisint oder None, Standard: None
Wenn es sich um eine ganze Zahl handelt, ist dies die Achse des Eingabearrays, entlang der die Statistik berechnet wird. Die Statistik jedes Achsen-Slices (z. B. Zeile) der Eingabe erscheint dann in einem entsprechenden Element der Ausgabe. Wenn
None, wird die Eingabe vor der Berechnung der Statistik geglättet.- nan_policy{‘propagate’, ‘omit’, ‘raise’}
Definiert, wie Eingabe-NaNs behandelt werden.
propagate: Wenn ein NaN in der Achsen-Slice (z. B. Zeile) vorhanden ist, entlang der die Statistik berechnet wird, wird der entsprechende Eintrag der Ausgabe NaN sein.omit: NaNs werden bei der Berechnung weggelassen. Wenn im Achsen-Slice, entlang dem die Statistik berechnet wird, nicht genügend Daten verbleiben, wird der entsprechende Eintrag der Ausgabe NaN sein.raise: Wenn ein NaN vorhanden ist, wird einValueErrorausgelöst.
- keepdimsbool, Standard: False
Wenn dies auf True gesetzt ist, bleiben die reduzierten Achsen im Ergebnis als Dimensionen mit der Größe eins erhalten. Mit dieser Option wird das Ergebnis korrekt gegen das Eingabearray gestreut (broadcasted).
- Rückgabe:
- result
TheilslopesResult-Instanz Der Rückgabewert ist ein Objekt mit folgenden Attributen:
- slopefloat
Theil-Steigung.
- interceptfloat
Achsenabschnitt der Theil-Geraden.
- low_slopefloat
Untere Grenze des Konfidenzintervalls für die Steigung.
- high_slopefloat
Obere Grenze des Konfidenzintervalls für die Steigung.
- result
Siehe auch
siegelslopeseine ähnliche Technik unter Verwendung wiederholter Mediane
Hinweise
Die Implementierung von
theilslopesfolgt [1]. Der Achsenabschnitt ist in [1] nicht definiert, und hier wird er alsmedian(y) - slope*median(x)definiert, wie in [3] angegeben. Andere Definitionen des Achsenabschnitts existieren in der Literatur, wie z. B.median(y - slope*x)in [4]. Die Vorgehensweise zur Berechnung des Achsenabschnitts kann durch den Parametermethodbestimmt werden. Ein Konfidenzintervall für den Achsenabschnitt wird nicht angegeben, da diese Frage in [1] nicht behandelt wird.Zur Kompatibilität mit älteren SciPy-Versionen verhält sich der Rückgabewert wie ein
namedtupleder Länge 4 mit den Feldernslope,intercept,low_slopeundhigh_slope, sodass man weiterhin schreiben kannslope, intercept, low_slope, high_slope = theilslopes(y, x)
Seit SciPy 1.9 werden
np.matrix-Eingaben (für neuen Code nicht empfohlen) vor der Berechnung innp.ndarraykonvertiert. In diesem Fall ist die Ausgabe eine Skalar- odernp.ndarraymit geeigneter Form anstelle eines 2D-np.matrix. Ebenso werden, während maskierte Elemente von Masked Arrays ignoriert werden, die Ausgabe eine Skalar- odernp.ndarrayanstelle eines Masked Arrays mitmask=Falsesein.Referenzen
[1] (1,2,3)P.K. Sen, „Estimates of the regression coefficient based on Kendall’s tau“, J. Am. Stat. Assoc., Vol. 63, S. 1379-1389, 1968.
[2]H. Theil, „A rank-invariant method of linear and polynomial regression analysis I, II and III“, Nederl. Akad. Wetensch., Proc. 53:, S. 386-392, S. 521-525, S. 1397-1412, 1950.
[3]W.L. Conover, „Practical nonparametric statistics“, 2. Aufl., John Wiley and Sons, New York, S. 493.
Beispiele
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt
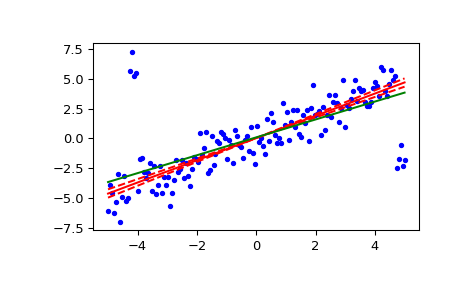
>>> x = np.linspace(-5, 5, num=150) >>> y = x + np.random.normal(size=x.size) >>> y[11:15] += 10 # add outliers >>> y[-5:] -= 7
Berechne die Steigung, den Achsenabschnitt und das 90%ige Konfidenzintervall. Zum Vergleich wird auch die Kleinste-Quadrate-Anpassung mit
linregressberechnet.>>> res = stats.theilslopes(y, x, 0.90, method='separate') >>> lsq_res = stats.linregress(x, y)
Zeichne die Ergebnisse. Die Theil-Sen-Regressionsgerade ist rot dargestellt, wobei die gestrichelten roten Linien das Konfidenzintervall der Steigung veranschaulichen (beachten Sie, dass die gestrichelten roten Linien nicht das Konfidenzintervall der Regression sind, da das Konfidenzintervall des Achsenabschnitts nicht enthalten ist). Die grüne Linie zeigt zum Vergleich die Kleinste-Quadrate-Anpassung.
>>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> ax.plot(x, y, 'b.') >>> ax.plot(x, res[1] + res[0] * x, 'r-') >>> ax.plot(x, res[1] + res[2] * x, 'r--') >>> ax.plot(x, res[1] + res[3] * x, 'r--') >>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-') >>> plt.show()