scipy.stats.

yeojohnson#

scipy.stats.yeojohnson(x, lmbda=None)[Quelle]#

Gibt einen Datensatz zurück, der durch eine Yeo-Johnson-Potenztransformation transformiert wurde.

Parameter:

xndarray: Eingabearray. Sollte eindimensional sein.
lmbdafloat, optional: Wenn lmbda None ist, wird das Lambda gefunden, das die Log-Likelihood-Funktion maximiert, und als zweites Ausgabeargument zurückgegeben. Andernfalls erfolgt die Transformation für den gegebenen Wert.

Rückgabe:

yeojohnson: ndarray: Yeo-Johnson Potenz-transformiertes Array.
maxlogfloat, optional: Wenn der Parameter lmbda None ist, ist das zweite zurückgegebene Argument das Lambda, das die Log-Likelihood-Funktion maximiert.

Siehe auch

probplot, yeojohnson_normplot, yeojohnson_normmax, yeojohnson_llf, boxcox

Hinweise

Die Yeo-Johnson-Transformation ist gegeben durch

\[\begin{split}y = \begin{cases} \frac{(x + 1)^\lambda - 1}{\lambda}, &\text{für } x \geq 0, \lambda \neq 0 \\ \log(x + 1), &\text{für } x \geq 0, \lambda = 0 \\ -\frac{(-x + 1)^{2 - \lambda} - 1}{2 - \lambda}, &\text{für } x < 0, \lambda \neq 2 \\ -\log(-x + 1), &\text{für } x < 0, \lambda = 2 \end{cases}\end{split}\]

Im Gegensatz zu boxcox erfordert yeojohnson nicht, dass die Eingabedaten positiv sind.

Hinzugefügt in Version 1.2.0.

Referenzen

I. Yeo und R.A. Johnson, „A New Family of Power Transformations to Improve Normality or Symmetry“, Biometrika 87.4 (2000)

Beispiele

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

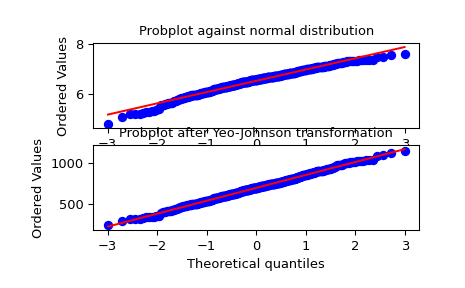
Wir generieren einige Zufallsvariaten aus einer nicht-normalen Verteilung und erstellen eine Wahrscheinlichkeitsdarstellung davon, um zu zeigen, dass sie in den Ausläufern nicht normal ist.

>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> x = stats.loggamma.rvs(5, size=500) + 5
>>> prob = stats.probplot(x, dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')

Wir verwenden nun yeojohnson, um die Daten so zu transformieren, dass sie der Normalverteilung am nächsten kommen.

>>> ax2 = fig.add_subplot(212)
>>> xt, lmbda = stats.yeojohnson(x)
>>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2)
>>> ax2.set_title('Probplot after Yeo-Johnson transformation')

>>> plt.show()

../../_images/scipy-stats-yeojohnson-1.png