scipy.differentiate.

derivative#

scipy.differentiate.derivative(f, x, *, args=(), tolerances=None, maxiter=10, order=8, initial_step=0.5, step_factor=2.0, step_direction=0, preserve_shape=False, callback=None)[Quelle]#

Numerische Auswertung der Ableitung einer elementweisen, reellen Skalarfunktion.

Für jedes Element der Ausgabe von f approximiert derivative die erste Ableitung von f am entsprechenden Element von x unter Verwendung der finiten Differenzen-Differentiation.

Diese Funktion arbeitet elementweise, wenn x, step_direction und args (broadcast-fähige) Arrays enthalten.

Parameter:

faufrufbar

Die Funktion, deren Ableitung gewünscht wird. Die Signatur muss lauten

f(xi: ndarray, *argsi) -> ndarray

wobei jedes Element von xi eine endliche reelle Zahl ist und argsi ein Tupel ist, das eine beliebige Anzahl von Arrays enthalten kann, die mit xi broadcast-fähig sind. f muss eine elementweise Funktion sein: jedes Skalarelement f(xi)[j] muss gleich f(xi[j]) für gültige Indizes j sein. Sie darf das Array xi oder die Arrays in argsi nicht verändern.

xFloat-Array-ähnlich

Abzissen, an denen die Ableitung ausgewertet werden soll. Müssen mit args und step_direction broadcast-fähig sein.

argstuple of array_like, optional

Zusätzliche positionale Array-Argumente, die an f übergeben werden. Arrays müssen untereinander und mit den Arrays von init broadcastfähig sein. Wenn die aufgerufene Funktion, für die die Wurzel gesucht wird, Argumente benötigt, die nicht mit x broadcastfähig sind, wrappen Sie diese Funktion mit f, sodass f nur x und broadcastfähige *args akzeptiert.

tolerancesDictionary von Floats, optional

Absolute und relative Toleranzen. Gültige Schlüssel des Dictionaries sind

atol - absolute Toleranz für die Ableitung
rtol - relative Toleranz für die Ableitung

Die Iteration wird gestoppt, wenn res.error < atol + rtol * abs(res.df). Die Standardwerte für atol ist die kleinste normale Zahl des entsprechenden Datentyps, und der Standardwert für rtol ist die Quadratwurzel der Präzision des entsprechenden Datentyps.

orderInteger, Standard: 8

Die (positive ganze Zahl) Ordnung der zu verwendenden Finite-Differenzen-Formel. Ungerade ganze Zahlen werden auf die nächste gerade ganze Zahl aufgerundet.

initial_stepfloat array_like, default: 0.5

Die (absolute) anfängliche Schrittgröße für die Approximation der Ableitung mittels finiter Differenzen.

step_factorFloat, Standard: 2.0

Der Faktor, um den die Schrittgröße in jeder Iteration *reduziert* wird; d. h. die Schrittgröße in Iteration 1 ist initial_step/step_factor. Wenn step_factor < 1, sind nachfolgende Schritte größer als der anfängliche Schritt; dies kann nützlich sein, wenn Schritte, die kleiner als ein bestimmter Schwellenwert sind, unerwünscht sind (z. B. aufgrund von subtraktiven Fehler).

maxiterInteger, Standard: 10

Die maximale Anzahl von Iterationen, die der Algorithmus durchführen soll. Siehe Hinweise.

step_directioninteger array_like

Ein Array, das die Richtung der finiten Differenzschritte repräsentiert (für den Fall, dass x nahe der Grenze des Funktionsbereichs liegt). Wenn 0 (Standard), werden zentrale Differenzen verwendet; wenn negativ (z.B. -1), sind die Schritte nicht-positiv; und wenn positiv (z.B. 1), sind alle Schritte nicht-negativ. Muss mit x und allen args broadcast-fähig sein.

preserve_shapebool, default: False

Im Folgenden bezieht sich „Argumente von f“ auf das Array xi und alle Arrays innerhalb von argsi. Sei shape die gebroadcastete Form von x und allen Elementen von args (was konzeptionell von xi` und ``argsi, die in f übergeben werden, getrennt ist).

Wenn preserve_shape=False (Standard), muss f Argumente beliebiger broadcast-fähiger Formen akzeptieren.
Wenn preserve_shape=True, muss f Argumente der Form shape *oder* shape + (n,) akzeptieren, wobei (n,) die Anzahl der Abzissen ist, an denen die Funktion ausgewertet wird.

In beiden Fällen muss das von f zurückgegebene Array für jedes Skalarelement xi[j] innerhalb von xi das Skalar f(xi[j]) an derselben Stelle enthalten. Folglich ist die Form der Ausgabe immer die Form der Eingabe xi.

Siehe Beispiele.

callbackcallable, optional

Eine optionale benutzerdefinierte Funktion, die vor der ersten Iteration und nach jeder Iteration aufgerufen wird. Aufgerufen als callback(res), wobei res ein _RichResult ist, ähnlich dem von derivative zurückgegebenen (aber die aktuellen Werte aller Variablen der Iteration enthält). Wenn callback eine StopIteration auslöst, wird der Algorithmus sofort beendet und derivative gibt ein Ergebnis zurück. callback darf res oder seine Attribute nicht verändern.

Rückgabe:

res_RichResult

Ein Objekt, das einer Instanz von scipy.optimize.OptimizeResult ähnelt, mit den folgenden Attributen. Die Beschreibungen sind so formuliert, als wären die Werte Skalare; wenn f jedoch ein Array zurückgibt, sind die Ausgaben Arrays derselben Form.

successBool-Array

True, wenn der Algorithmus erfolgreich beendet wurde (Status 0); andernfalls False.

statusInteger-Array

Eine Ganzzahl, die den Exit-Status des Algorithmus darstellt.

0 : Der Algorithmus konvergierte gegen die angegebenen Toleranzen.
-1 : Die Fehlerschätzung stieg an, daher wurde die Iteration beendet.
-2 : Die maximale Anzahl von Iterationen wurde erreicht.
-3 : Ein nicht-endlicher Wert wurde angetroffen.
-4 : Die Iteration wurde durch callback beendet.
1 : Der Algorithmus läuft normal (nur in callback).

dffloat array

Die Ableitung von f an x, wenn der Algorithmus erfolgreich beendet wurde.

errorFloat-Array

Eine Schätzung des Fehlers: der Betrag der Differenz zwischen der aktuellen Schätzung der Ableitung und der Schätzung in der vorherigen Iteration.

nitint array

Die Anzahl der Iterationen des Algorithmus, die durchgeführt wurden.

nfevInteger-Array

Die Anzahl der Punkte, an denen f ausgewertet wurde.

xfloat array

Der Wert, an dem die Ableitung von f ausgewertet wurde (nach Broadcasting mit args und step_direction).

Siehe auch

jacobian, hessian

Hinweise

Die Implementierung wurde von jacobi [1], numdifftools [2] und DERIVEST [3] inspiriert, aber die Implementierung folgt der Theorie der Taylorreihen direkter (und wohl naiv). In der ersten Iteration wird die Ableitung mithilfe einer finiten Differenzenformel der Ordnung order mit einer maximalen Schrittgröße von initial_step geschätzt. In jeder nachfolgenden Iteration wird die maximale Schrittgröße um step_factor reduziert und die Ableitung erneut geschätzt, bis eine Abbruchbedingung erreicht ist. Die Fehlerschätzung ist der Betrag der Differenz zwischen der aktuellen Ableitungsapproximation und der der vorherigen Iteration.

Die Stencils der finiten Differenzenformeln sind so konzipiert, dass die Abzissen „verschachtelt“ sind: nachdem f in der ersten Iteration an order + 1 Punkten ausgewertet wurde, wird f in jeder nachfolgenden Iteration nur noch an zwei neuen Punkten ausgewertet; order - 1 zuvor ausgewertete Funktionswerte, die für die finiten Differenzenformel benötigt werden, werden wiederverwendet, und zwei Funktionswerte (Auswertungen an den Punkten, die am weitesten von x entfernt sind) werden nicht verwendet.

Schrittgrößen sind absolut. Wenn die Schrittgröße im Verhältnis zur Größe von x klein ist, geht Präzision verloren; zum Beispiel, wenn x 1e20 ist, kann die Standard-Anfangsschrittgröße von 0.5 nicht aufgelöst werden. Daher sollten für große Beträge von x größere Anfangsschrittgrößen in Betracht gezogen werden.

Die Standardtoleranzen sind schwer zu erfüllen, wenn die tatsächliche Ableitung exakt Null ist. Wenn die Ableitung exakt Null sein kann, sollten Sie eine absolute Toleranz (z.B. atol=1e-12) angeben, um die Konvergenz zu verbessern.

Referenzen

[1]

Hans Dembinski (@HDembinski). jacobi. HDembinski/jacobi

[2]

Per A. Brodtkorb und John D’Errico. numdifftools. https://numdifftools.readthedocs.io/en/latest/

[3]

John D’Errico. DERIVEST: Adaptive Robust Numerical Differentiation. https://www.mathworks.com/matlabcentral/fileexchange/13490-adaptive-robust-numerical-differentiation

[4]

Numerische Differentiation. Wikipedia. https://en.wikipedia.org/wiki/Numerical_differentiation

Beispiele

Auswertung der Ableitung von np.exp an mehreren Punkten x.

>>> import numpy as np
>>> from scipy.differentiate import derivative
>>> f = np.exp
>>> df = np.exp  # true derivative
>>> x = np.linspace(1, 2, 5)
>>> res = derivative(f, x)
>>> res.df  # approximation of the derivative
array([2.71828183, 3.49034296, 4.48168907, 5.75460268, 7.3890561 ])
>>> res.error  # estimate of the error
array([7.13740178e-12, 9.16600129e-12, 1.17594823e-11, 1.51061386e-11,
       1.94262384e-11])
>>> abs(res.df - df(x))  # true error
array([2.53130850e-14, 3.55271368e-14, 5.77315973e-14, 5.59552404e-14,
       6.92779167e-14])

Zeigt die Konvergenz der Approximation, während die Schrittgröße reduziert wird. Bei jeder Iteration wird die Schrittgröße um den Faktor step_factor reduziert, sodass für eine ausreichend kleine Anfangsschrittgröße jede Iteration den Fehler um den Faktor 1/step_factor**order reduziert, bis die begrenzte Genauigkeit der Arithmetik weitere Verbesserungen verhindert.

>>> import matplotlib.pyplot as plt
>>> iter = list(range(1, 12))  # maximum iterations
>>> hfac = 2  # step size reduction per iteration
>>> hdir = [-1, 0, 1]  # compare left-, central-, and right- steps
>>> order = 4  # order of differentiation formula
>>> x = 1
>>> ref = df(x)
>>> errors = []  # true error
>>> for i in iter:
...     res = derivative(f, x, maxiter=i, step_factor=hfac,
...                      step_direction=hdir, order=order,
...                      # prevent early termination
...                      tolerances=dict(atol=0, rtol=0))
...     errors.append(abs(res.df - ref))
>>> errors = np.array(errors)
>>> plt.semilogy(iter, errors[:, 0], label='left differences')
>>> plt.semilogy(iter, errors[:, 1], label='central differences')
>>> plt.semilogy(iter, errors[:, 2], label='right differences')
>>> plt.xlabel('iteration')
>>> plt.ylabel('error')
>>> plt.legend()
>>> plt.show()

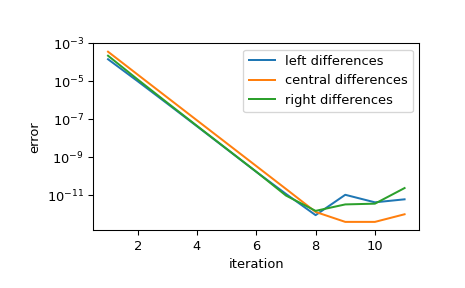
../../_images/scipy-differentiate-derivative-1_00_00.png

>>> (errors[1, 1] / errors[0, 1], 1 / hfac**order)
(0.06215223140159822, 0.0625)

Die Implementierung ist über x, step_direction und args vektorisiert. Die Funktion wird einmal vor der ersten Iteration ausgewertet, um die Eingabevalidierung und -standardisierung durchzuführen, und danach einmal pro Iteration.

>>> def f(x, p):
...     f.nit += 1
...     return x**p
>>> f.nit = 0
>>> def df(x, p):
...     return p*x**(p-1)
>>> x = np.arange(1, 5)
>>> p = np.arange(1, 6).reshape((-1, 1))
>>> hdir = np.arange(-1, 2).reshape((-1, 1, 1))
>>> res = derivative(f, x, args=(p,), step_direction=hdir, maxiter=1)
>>> np.allclose(res.df, df(x, p))
True
>>> res.df.shape
(3, 5, 4)
>>> f.nit
2

Standardmäßig ist preserve_shape False, und daher kann der aufrufbare f mit Arrays beliebiger broadcast-fähiger Formen aufgerufen werden. Zum Beispiel

>>> shapes = []
>>> def f(x, c):
...    shape = np.broadcast_shapes(x.shape, c.shape)
...    shapes.append(shape)
...    return np.sin(c*x)
>>>
>>> c = [1, 5, 10, 20]
>>> res = derivative(f, 0, args=(c,))
>>> shapes
[(4,), (4, 8), (4, 2), (3, 2), (2, 2), (1, 2)]

Um zu verstehen, woher diese Formen stammen – und um besser zu verstehen, wie derivative genaue Ergebnisse berechnet – beachten Sie, dass höhere Werte von c mit höherfrequenten Sinusoiden korrespondieren. Die höherfrequenten Sinusoide lassen die Ableitung der Funktion schneller ändern, sodass mehr Funktionsauswertungen erforderlich sind, um die Zielgenauigkeit zu erreichen.

>>> res.nfev
array([11, 13, 15, 17], dtype=int32)

Die anfängliche shape, (4,), entspricht der Auswertung der Funktion an einer einzelnen Abzisse und allen vier Frequenzen; dies wird zur Eingabevalidierung und zur Bestimmung der Größe und des Datentyps der Arrays, die Ergebnisse speichern, verwendet. Die nächste Form entspricht der Auswertung der Funktion an einem anfänglichen Gitter von Abzissen und allen vier Frequenzen. Nachfolgende Aufrufe der Funktion werten die Funktion an zwei weiteren Abzissen aus, wodurch die effektive Ordnung der Approximation um zwei erhöht wird. In späteren Funktionsauswertungen wird die Funktion jedoch an weniger Frequenzen ausgewertet, da ihre entsprechende Ableitung bereits die erforderliche Toleranz erreicht hat. Dies spart Funktionsauswertungen, um die Leistung zu verbessern, erfordert aber, dass die Funktion Argumente beliebiger Form akzeptiert.

„Vektorwertige“ Funktionen erfüllen diese Anforderung wahrscheinlich nicht. Betrachten Sie zum Beispiel

>>> def f(x):
...    return [x, np.sin(3*x), x+np.sin(10*x), np.sin(20*x)*(x-1)**2]

Dieser Integrand ist mit derivative in seiner aktuellen Form nicht kompatibel; zum Beispiel wird die Form der Ausgabe nicht die gleiche sein wie die Form von x. Eine solche Funktion *könnte* mit der Einführung zusätzlicher Parameter in eine kompatible Form umgewandelt werden, aber dies wäre umständlich. In solchen Fällen wäre die Einführung von preserve_shape eine einfachere Lösung.

>>> shapes = []
>>> def f(x):
...     shapes.append(x.shape)
...     x0, x1, x2, x3 = x
...     return [x0, np.sin(3*x1), x2+np.sin(10*x2), np.sin(20*x3)*(x3-1)**2]
>>>
>>> x = np.zeros(4)
>>> res = derivative(f, x, preserve_shape=True)
>>> shapes
[(4,), (4, 8), (4, 2), (4, 2), (4, 2), (4, 2)]

Hier ist die Form von x (4,). Mit preserve_shape=True kann die Funktion mit dem Argument x der Form (4,) oder (4, n) aufgerufen werden, und das beobachten wir auch.