scipy.integrate.

odeint

scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

Integrieren Sie ein System von gewöhnlichen Differentialgleichungen.

Hinweis

Für neuen Code verwenden Sie bitte scipy.integrate.solve_ivp, um eine Differentialgleichung zu lösen.

Löst ein System von gewöhnlichen Differentialgleichungen mit lsoda aus der FORTRAN-Bibliothek odepack.

Löst das Anfangswertproblem für steife oder nicht steife Systeme von Differentialgleichungen erster Ordnung

dy/dt = func(y, t, ...)  [or func(t, y, ...)]

wobei y ein Vektor sein kann.

Hinweis

Standardmäßig sind die Argumente der ersten beiden Argumente von func in umgekehrter Reihenfolge zu den Argumenten in der Systemdefinitionsfunktion, die von der Klasse scipy.integrate.ode und der Funktion scipy.integrate.solve_ivp verwendet wird. Um eine Funktion mit der Signatur func(t, y, ...) zu verwenden, muss das Argument tfirst auf True gesetzt werden.

Parameter:

funccallable(y, t, …) oder callable(t, y, …)

Berechnet die Ableitung von y nach t. Wenn die Signatur callable(t, y, ...) ist, muss das Argument tfirst auf True gesetzt werden. func darf die Daten in y nicht ändern, da es sich um eine Ansicht der intern vom ODE-Solver verwendeten Daten handelt.

y0array

Anfangsbedingung für y (kann ein Vektor sein).

tarray

Eine Sequenz von Zeitpunkten, für die y gelöst werden soll. Der Anfangswertpunkt sollte das erste Element dieser Sequenz sein. Diese Sequenz muss monoton steigend oder monoton fallend sein; wiederholte Werte sind zulässig.

argstuple, optional

Zusätzliche Argumente, die an die Funktion übergeben werden sollen.

Dfuncallable(y, t, …) oder callable(t, y, …)

Gradient (Jacobi-Matrix) von func. Wenn die Signatur callable(t, y, ...) ist, muss das Argument tfirst auf True gesetzt werden. Dfun darf die Daten in y nicht ändern, da es sich um eine Ansicht der intern vom ODE-Solver verwendeten Daten handelt.

col_derivbool, optional

True, wenn Dfun Ableitungen spaltenweise definiert (schneller), andernfalls sollte Dfun Ableitungen zeilenweise definieren.

full_outputbool, optional

True, wenn ein Wörterbuch mit optionalen Ausgaben als zweite Ausgabe zurückgegeben werden soll

printmessgbool, optional

Ob die Konvergenzmeldung gedruckt werden soll

tfirstbool, optional

Wenn True, müssen die ersten beiden Argumente von func (und Dfun, falls gegeben) t, y anstelle des Standardwerts y, t sein.

Hinzugefügt in Version 1.1.0.

Rückgabe:

yarray, shape (len(t), len(y0))

Array, das den Wert von y für jeden gewünschten Zeitpunkt in t enthält, mit dem Anfangswert y0 in der ersten Zeile.

infodictdict, nur zurückgegeben, wenn full_output == True

Wörterbuch mit zusätzlichen Auskunftsinformationen

Schlüssel	Bedeutung
„hu“	Vektor der Schrittgrößen, die für jeden Zeitschritt erfolgreich verwendet wurden
„tcur“	Vektor mit dem erreichten t-Wert für jeden Zeitschritt (wird immer mindestens so groß sein wie die Eingangszeiten)
„tolsf“	Vektor der Toleranz-Skalierungsfaktoren, größer als 1.0, berechnet, wenn eine zu hohe Genauigkeit angefordert wurde
„tsw“	Zeitpunkt t des letzten Methodenwechsels (angegeben für jeden Zeitschritt)
„nst“	kumulative Anzahl der Zeitschritte
„nfe“	kumulative Anzahl der Funktionsauswertungen für jeden Zeitschritt
„nje“	kumulative Anzahl der Jacobi-Matrix-Auswertungen für jeden Zeitschritt
„nqu“	ein Vektor der Methodenordnungen für jeden erfolgreichen Schritt
„imxer“	Index der Komponente mit dem größten Betrag im gewichteten lokalen Fehlervektor (e / ewt) bei einem Fehlerereignis, sonst -1
„lenrw“	die Länge des benötigten Double-Work-Arrays
„leniw“	die Länge des benötigten Integer-Work-Arrays
„mused“	ein Vektor von Methodenindikatoren für jeden erfolgreichen Zeitschritt: 1: Adams (nicht steif), 2: BDF (steif)

Andere Parameter:

ml, muint, optional

Wenn einer davon nicht None oder nicht-negativ ist, wird angenommen, dass die Jacobi-Matrix bandförmig ist. Diese geben die Anzahl der unteren und oberen Nicht-Null-Diagonalen in dieser bandförmigen Matrix an. Für den bandförmigen Fall sollte Dfun eine Matrix zurückgeben, deren Zeilen die Nicht-Null-Bänder enthalten (beginnend mit der untersten Diagonalen). Daher sollte die Rückgabematrix jac von Dfun die Form (ml + mu + 1, len(y0)) haben, wenn ml >=0 oder mu >=0. Die Daten in jac müssen so gespeichert werden, dass jac[i - j + mu, j] die Ableitung der i-ten Gleichung nach der j-ten Zustandsvariable enthält. Wenn col_deriv True ist, muss die Transponierte dieser jac zurückgegeben werden.

rtol, atolfloat, optional

Die Eingabeparameter rtol und atol bestimmen die vom Solver durchgeführte Fehlerkontrolle. Der Solver kontrolliert den Vektor e der geschätzten lokalen Fehler in y gemäß einer Ungleichung der Form max-norm von (e / ewt) <= 1, wobei ewt ein Vektor positiver Fehlergewichte ist, der als ewt = rtol * abs(y) + atol berechnet wird. rtol und atol können entweder Vektoren gleicher Länge wie y oder Skalare sein. Standardwert ist 1.49012e-8.

tcritndarray, optional

Vektor von kritischen Punkten (z. B. Singularitäten), bei denen die Integration sorgfältig erfolgen sollte.

h0float, (0: vom Solver bestimmt), optional

Die Schrittgröße, die beim ersten Schritt versucht werden soll.

hmaxfloat, (0: vom Solver bestimmt), optional

Die maximal zulässige absolute Schrittgröße.

hminfloat, (0: vom Solver bestimmt), optional

Die minimal zulässige absolute Schrittgröße.

ixprbool, optional

Ob zusätzliche Ausgaben bei Methodenwechseln generiert werden sollen.

mxstepint, (0: vom Solver bestimmt), optional

Maximale Anzahl von (intern definierten) Schritten, die für jeden Integrationspunkt in t zulässig sind.

mxhnilint, (0: vom Solver bestimmt), optional

Maximale Anzahl der gedruckten Meldungen.

mxordnint, (0: vom Solver bestimmt), optional

Maximale Ordnung, die für die nicht steife (Adams) Methode zulässig ist.

mxordsint, (0: vom Solver bestimmt), optional

Maximale Ordnung, die für die steife (BDF) Methode zulässig ist.

Siehe auch

solve_ivp

Löst ein Anfangswertproblem für ein System von ODEs

ode

ein objektorientierterer Integrator basierend auf VODE

quad

zum Finden der Fläche unter einer Kurve

Beispiele

Probieren Sie es in Ihrem Browser aus!

Die Differentialgleichung zweiter Ordnung für den Winkel theta eines Pendels, das der Schwerkraft mit Reibung ausgesetzt ist, kann geschrieben werden als

theta''(t) + b*theta'(t) + c*sin(theta(t)) = 0

wobei b und c positive Konstanten sind und ein Apostroph (’) eine Ableitung bezeichnet. Um diese Gleichung mit odeint zu lösen, müssen wir sie zuerst in ein System von Gleichungen erster Ordnung umwandeln. Durch Definition der Winkelgeschwindigkeit omega(t) = theta'(t) erhalten wir das System

theta'(t) = omega(t)
omega'(t) = -b*omega(t) - c*sin(theta(t))

Sei y der Vektor [theta, omega]. Wir implementieren dieses System in Python wie folgt:

>>> import numpy as np
>>> def pend(y, t, b, c):
...     theta, omega = y
...     dydt = [omega, -b*omega - c*np.sin(theta)]
...     return dydt
...

Wir gehen davon aus, dass die Konstanten b = 0.25 und c = 5.0 sind.

>>> b = 0.25
>>> c = 5.0

Für Anfangsbedingungen nehmen wir an, dass das Pendel fast senkrecht steht mit theta(0) = pi - 0.1 und sich anfangs in Ruhe befindet, also omega(0) = 0. Dann ist der Vektor der Anfangsbedingungen:

>>> y0 = [np.pi - 0.1, 0.0]

Wir werden eine Lösung an 101 gleichmäßig verteilten Abtastpunkten im Intervall 0 <= t <= 10 erzeugen. Unser Zeitarray ist also:

>>> t = np.linspace(0, 10, 101)

Rufen Sie odeint auf, um die Lösung zu erzeugen. Um die Parameter b und c an pend zu übergeben, übergeben wir sie mit dem Argument args an odeint.

>>> from scipy.integrate import odeint
>>> sol = odeint(pend, y0, t, args=(b, c))

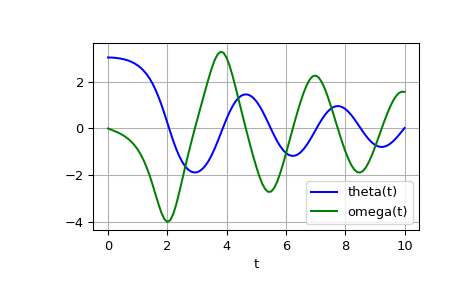
Die Lösung ist ein Array der Form (101, 2). Die erste Spalte ist theta(t) und die zweite ist omega(t). Der folgende Code zeichnet beide Komponenten auf.

>>> import matplotlib.pyplot as plt
>>> plt.plot(t, sol[:, 0], 'b', label='theta(t)')
>>> plt.plot(t, sol[:, 1], 'g', label='omega(t)')
>>> plt.legend(loc='best')
>>> plt.xlabel('t')
>>> plt.grid()
>>> plt.show()

ZurückIn Tab öffnen