scipy.integrate.

quad_vec

scipy.integrate.quad_vec(f, a, b, epsabs=1e-200, epsrel=1e-08, norm='2', cache_size=100000000.0, limit=10000, workers=1, points=None, quadrature=None, full_output=False, *, args=())

Adaptive Integration einer vektorwertigen Funktion.

Parameter:

faufrufbar

Vektorwertige Funktion f(x) zum Integrieren.

afloat

Anfangspunkt.

bfloat

Endpunkt.

epsabsfloat, optional

Absolute Toleranz.

epsrelfloat, optional

Relative Toleranz.

norm{‘max’, ‘2’}, optional

Vektornorm zur Fehlerabschätzung.

cache_sizeint, optional

Anzahl der Bytes, die für die Memoisation verwendet werden sollen.

limitfloat oder int, optional

Eine Obergrenze für die Anzahl der Unterintervalle, die im adaptiven Algorithmus verwendet werden.

workersint oder Map-ähnliches aufrufbare Objekt, optional

Wenn workers eine Ganzzahl ist, wird ein Teil der Berechnung parallel unterteilt in diese Anzahl von Aufgaben (unter Verwendung von multiprocessing.pool.Pool). Geben Sie -1 an, um alle verfügbaren Kerne zu verwenden. Alternativ können Sie eine Map-ähnliche aufrufbare Funktion angeben, z. B. multiprocessing.pool.Pool.map zur parallelen Auswertung der Population. Diese Auswertung wird als workers(func, iterable) durchgeführt.

pointslist, optional

Liste zusätzlicher Bruchpunkte.

quadrature{‘gk21’, ‘gk15’, ‘trapezoid’}, optional

Quadraturregel, die auf Unterintervallen verwendet werden soll. Optionen: ‘gk21’ (Gauss-Kronrod 21-Punkt-Regel), ‘gk15’ (Gauss-Kronrod 15-Punkt-Regel), ‘trapezoid’ (zusammengesetzte Trapezregel). Standard: ‘gk21’ für endliche Intervalle und ‘gk15’ für (halb-)unendliche.

full_outputbool, optional

Gibt ein zusätzliches info Objekt zurück.

argstuple, optional

Zusätzliche Argumente, die an die Funktion übergeben werden sollen, falls vorhanden.

Hinzugefügt in Version 1.8.0.

Rückgabe:

res{float, array-like}

Schätzung für das Ergebnis

errfloat

Fehlerschätzung für das Ergebnis in der gegebenen Norm

infoobject

Wird nur zurückgegeben, wenn full_output=True ist. Ergebnisobjekt mit den Attributen

successbool

Ob die Integration die Zielgenauigkeit erreicht hat.

statusint

Indikator für Konvergenz, Erfolg (0), Fehler (1) und Fehler aufgrund von Rundungsfehlern (2).

nevalint

Anzahl der Funktionsauswertungen.

intervalsndarray, shape (num_intervals, 2)

Start- und Endpunkte der Unterteilungsintervalle.

integralsndarray, shape (num_intervals, …)

Integral für jedes Intervall. Beachten Sie, dass maximal cache_size Werte aufgezeichnet werden und das Array für fehlende Elemente nan enthalten kann.

errorsndarray, shape (num_intervals,)

Geschätzter Integrationsfehler für jedes Intervall.

Hinweise

Der Algorithmus folgt hauptsächlich der Implementierung der DQAG*-Algorithmen von QUADPACK, die globale Fehlerkontrolle und adaptive Unterteilung implementieren.

Der Algorithmus weist einige Unterschiede zum QUADPACK-Ansatz auf.

Anstatt ein Intervall nach dem anderen zu unterteilen, unterteilt der Algorithmus N Intervalle mit den größten Fehlern gleichzeitig. Dies ermöglicht (teilweise) Parallelisierung der Integration.

Die Logik, zuerst "das nächstgrößte" Intervall zu unterteilen, wird dann nicht implementiert, und wir verlassen uns auf die obige Erweiterung, um zu vermeiden, dass wir uns nur auf "kleine" Intervalle konzentrieren.

Die Wynn-Epsilon-Tabellenextrapolation wird nicht verwendet (QUADPACK verwendet sie für unendliche Intervalle). Dies liegt daran, dass der Algorithmus hier für vektorwertige Funktionen in einer vom Benutzer spezifizierten Norm funktionieren soll und die Erweiterung des Epsilon-Algorithmus für diesen Fall scheinbar nicht allgemein vereinbart ist. Für die Max-Norm könnte elementweise Wynn-Epsilon möglich sein, aber wir tun dies hier nicht in der Hoffnung, dass die Epsilon-Extrapolation hauptsächlich in Sonderfällen nützlich ist.

Referenzen

[1] R. Piessens, E. de Doncker, QUADPACK (1983).

Beispiele

Probieren Sie es in Ihrem Browser aus!

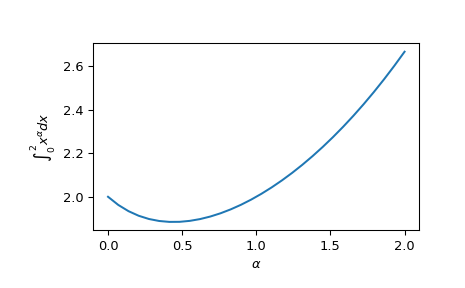
Wir können Integrationen einer vektorwertigen Funktion berechnen.

>>> from scipy.integrate import quad_vec
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> alpha = np.linspace(0.0, 2.0, num=30)
>>> f = lambda x: x**alpha
>>> x0, x1 = 0, 2
>>> y, err = quad_vec(f, x0, x1)
>>> plt.plot(alpha, y)
>>> plt.xlabel(r"$\alpha$")
>>> plt.ylabel(r"$\int_{0}^{2} x^\alpha dx$")
>>> plt.show()

Bei Verwendung des Arguments workers sollte sichergestellt werden, dass das Hauptmodul import-sicher ist, z. B. indem das obige Beispiel wie folgt umgeschrieben wird:

from scipy.integrate import quad_vec
import numpy as np
import matplotlib.pyplot as plt

alpha = np.linspace(0.0, 2.0, num=30)
x0, x1 = 0, 2
def f(x):
    return x**alpha

if __name__ == "__main__":
    y, err = quad_vec(f, x0, x1, workers=2)

ZurückIn Tab öffnen