scipy.integrate.

solve_bvp#

scipy.integrate.solve_bvp(fun, bc, x, y, p=None, S=None, fun_jac=None, bc_jac=None, tol=0.001, max_nodes=1000, verbose=0, bc_tol=None)[Quelle]#

Löst ein Randwertproblem für ein System von ODEs.

Diese Funktion löst numerisch ein System von Differentialgleichungen erster Ordnung, das mit Randbedingungen an zwei Punkten belegt ist.

dy / dx = f(x, y, p) + S * y / (x - a), a <= x <= b
bc(y(a), y(b), p) = 0

Hier ist x eine 1D-unabhängige Variable, y(x) eine nD-vektorwertige Funktion und p ein kD-Vektor unbekannter Parameter, die zusammen mit y(x) gefunden werden sollen. Damit das Problem bestimmt ist, muss es n + k Randbedingungen geben, d. h. bc muss eine (n + k)D-Funktion sein.

Der letzte singuläre Term auf der rechten Seite des Systems ist optional. Er wird durch eine n-mal-n-Matrix S definiert, sodass die Lösung S y(a) = 0 erfüllen muss. Diese Bedingung wird während der Iterationen erzwungen und darf daher nicht im Widerspruch zu den Randbedingungen stehen. Siehe [2] für eine Erklärung, wie dieser Term bei der numerischen Lösung von BVPs behandelt wird.

Probleme in einem komplexen Bereich können ebenfalls gelöst werden. In diesem Fall werden y und p als komplex betrachtet und f und bc als komplexwertige Funktionen angenommen, x bleibt jedoch reell. Beachten Sie, dass f und bc komplex differenzierbar sein müssen (Cauchy-Riemann-Gleichungen erfüllen, siehe [4]), andernfalls sollten Sie Ihr Problem für die reellen und imaginären Teile separat umschreiben. Um ein Problem in einem komplexen Bereich zu lösen, übergeben Sie eine anfängliche Schätzung für y mit einem komplexen Datentyp (siehe unten).

Parameter:

funcallable

Rechte Seite des Systems. Die Aufrufsignatur lautet fun(x, y) oder fun(x, y, p), falls Parameter vorhanden sind. Alle Argumente sind ndarray: x mit Form (m,), y mit Form (n, m), was bedeutet, dass y[:, i] zu x[i] korrespondiert, und p mit Form (k,). Der Rückgabewert muss ein Array mit Form (n, m) und demselben Layout wie y sein.

bcaufrufbar

Funktion, die die Residuen der Randbedingungen auswertet. Die Aufrufsignatur lautet bc(ya, yb) oder bc(ya, yb, p), falls Parameter vorhanden sind. Alle Argumente sind ndarray: ya und yb mit Form (n,) und p mit Form (k,). Der Rückgabewert muss ein Array mit Form (n + k,) sein.

xarray_like, Form (m,)

Anfangsgitter. Muss eine streng aufsteigende Folge reeller Zahlen mit x[0]=a und x[-1]=b sein.

yarray_like, Form (n, m)

Anfängliche Schätzung für die Funktionswerte an den Gitterknoten, die i-te Spalte entspricht x[i]. Für Probleme in einem komplexen Bereich übergeben Sie y mit einem komplexen Datentyp (auch wenn die anfängliche Schätzung rein reell ist).

parray_like mit Form (k,) oder None, optional

Anfängliche Schätzung für die unbekannten Parameter. Wenn None (Standard), wird angenommen, dass das Problem von keinen Parametern abhängt.

Sarray_like mit Form (n, n) oder None

Matrix, die den singulären Term definiert. Wenn None (Standard), wird das Problem ohne den singulären Term gelöst.

fun_jacaufrufbar oder None, optional

Funktion, die Ableitungen von f nach y und p berechnet. Die Aufrufsignatur lautet fun_jac(x, y) oder fun_jac(x, y, p), falls Parameter vorhanden sind. Die Rückgabe muss 1 oder 2 Elemente in der folgenden Reihenfolge enthalten.

df_dy : array_like, Form (n, n, m), wobei ein Element (i, j, q) gleich d f_i(x_q, y_q, p) / d (y_q)_j ist.

df_dp : array_like, Form (n, k, m), wobei ein Element (i, j, q) gleich d f_i(x_q, y_q, p) / d p_j ist.

Hier nummeriert q die Knoten, an denen x und y definiert sind, während i und j die Vektorkomponenten nummerieren. Wenn das Problem ohne unbekannte Parameter gelöst wird, sollte df_dp nicht zurückgegeben werden.

Wenn fun_jac None ist (Standard), werden die Ableitungen durch Vorwärts-Finite-Differenzen geschätzt.

bc_jacaufrufbar oder None, optional

Funktion, die Ableitungen von bc nach ya, yb und p berechnet. Die Aufrufsignatur lautet bc_jac(ya, yb) oder bc_jac(ya, yb, p), falls Parameter vorhanden sind. Die Rückgabe muss 2 oder 3 Elemente in der folgenden Reihenfolge enthalten.

dbc_dya : array_like, Form (n, n), wobei ein Element (i, j) gleich d bc_i(ya, yb, p) / d ya_j ist.

dbc_dyb : array_like, Form (n, n), wobei ein Element (i, j) gleich d bc_i(ya, yb, p) / d yb_j ist.

dbc_dp : array_like, Form (n, k), wobei ein Element (i, j) gleich d bc_i(ya, yb, p) / d p_j ist.

Wenn das Problem ohne unbekannte Parameter gelöst wird, sollte dbc_dp nicht zurückgegeben werden.

Wenn bc_jac None ist (Standard), werden die Ableitungen durch Vorwärts-Finite-Differenzen geschätzt.

tolfloat, optional

Gewünschte Toleranz der Lösung. Wenn wir r = y' - f(x, y) definieren, wobei y die gefundene Lösung ist, dann versucht der Solver, auf jedem Gitterintervall norm(r / (1 + abs(f)) < tol zu erreichen, wobei norm in einem quadratischen Mittel (unter Verwendung einer numerischen Quadraturformel) geschätzt wird. Standard ist 1e-3.

max_nodesint, optional

Maximale zulässige Anzahl von Gitterknoten. Wenn überschritten, terminiert der Algorithmus. Standard ist 1000.

verbose{0, 1, 2}, optional

Level der Ausführlichkeit des Algorithmus

0 (Standard) : arbeitet leise.

1 : zeigt einen Beendigungsbericht an.

2 : Fortschritt während der Iterationen anzeigen.

bc_tolfloat, optional

Gewünschte absolute Toleranz für die Randbedingungsresiduen: bc Wert sollte komponentenweise abs(bc) < bc_tol erfüllen. Standardmäßig gleich tol. Bis zu 10 Iterationen sind erlaubt, um diese Toleranz zu erreichen.

Rückgabe:

Bunch-Objekt mit den folgenden definierten Feldern

solPPoly

Gefundene Lösung für y als scipy.interpolate.PPoly-Instanz, ein C1-kontinuierlicher kubischer Spline.

pndarray oder None, Form (k,)

Gefundene Parameter. None, wenn die Parameter nicht im Problem vorhanden waren.

xndarray, Form (m,)

Knoten des endgültigen Gitters.

yndarray, Form (n, m)

Lösungswerte an den Gitterknoten.

ypndarray, Form (n, m)

Ableitungen der Lösung an den Gitterknoten.

rms_residualsndarray, Form (m - 1,)

RMS-Werte der relativen Residuen über jedes Gitterintervall (siehe Beschreibung des tol-Parameters).

niterint

Anzahl der abgeschlossenen Iterationen.

statusint

Grund für die Beendigung des Algorithmus

0: Der Algorithmus hat die gewünschte Genauigkeit erreicht.

1: Die maximale Anzahl von Gitterknoten wurde überschritten.

2: Eine singuläre Jacobi-Matrix wurde bei der Lösung des Kollokationssystems angetroffen.

messagestring

Verbale Beschreibung des Abbruchgrundes.

successbool

True, wenn der Algorithmus die gewünschte Genauigkeit erreicht hat (status=0).

Hinweise

Diese Funktion implementiert einen Kollokationsalgorithmus 4. Ordnung mit Residualkontrolle, ähnlich wie in [1] beschrieben. Ein Kollokationssystem wird mit einer gedämpften Newton-Methode und einer affininvarianten Kriteriumsfunktion gelöst, wie in [3] beschrieben.

Beachten Sie, dass in [1] die integralen Residuen ohne Normierung durch die Intervalllängen definiert sind. Daher unterscheidet sich ihre Definition um einen Faktor von h**0.5 (h ist die Intervalllänge) von der hier verwendeten Definition.

Hinzugefügt in Version 0.18.0.

Referenzen

[1] (1,2)

J. Kierzenka, L. F. Shampine, “A BVP Solver Based on Residual Control and the Maltab PSE”, ACM Trans. Math. Softw., Vol. 27, Number 3, pp. 299-316, 2001.

[2]

L.F. Shampine, P. H. Muir and H. Xu, “A User-Friendly Fortran BVP Solver”, J. Numer. Anal., Ind. Appl. Math. (JNAIAM), Vol. 1, Number 2, pp. 201-217, 2006.

[3]

U. Ascher, R. Mattheij und R. Russell, “Numerical Solution of Boundary Value Problems for Ordinary Differential Equations”, Philidelphia, PA: Society for Industrial and Applied Mathematics, 1995. DOI:10.1137/1.9781611971231

[4]

Cauchy-Riemann-Gleichungen auf Wikipedia.

Beispiele

Im ersten Beispiel lösen wir das Bratu-Problem

y'' + k * exp(y) = 0
y(0) = y(1) = 0

für k = 1.

Wir schreiben die Gleichung als System erster Ordnung um und implementieren die Auswertung ihrer rechten Seite.

y1' = y2
y2' = -exp(y1)

>>> import numpy as np
>>> def fun(x, y):
...     return np.vstack((y[1], -np.exp(y[0])))

Implementieren Sie die Auswertung der Randbedingungsresiduen.

>>> def bc(ya, yb):
...     return np.array([ya[0], yb[0]])

Definieren Sie das anfängliche Gitter mit 5 Knoten.

>>> x = np.linspace(0, 1, 5)

Dieses Problem ist bekannt dafür, zwei Lösungen zu haben. Um beide zu erhalten, verwenden wir zwei verschiedene anfängliche Schätzungen für y. Wir bezeichnen sie mit den Indizes a und b.

>>> y_a = np.zeros((2, x.size))
>>> y_b = np.zeros((2, x.size))
>>> y_b[0] = 3

Nun sind wir bereit, den Solver auszuführen.

>>> from scipy.integrate import solve_bvp
>>> res_a = solve_bvp(fun, bc, x, y_a)
>>> res_b = solve_bvp(fun, bc, x, y_b)

Lassen Sie uns die beiden gefundenen Lösungen plotten. Wir nutzen die Tatsache, dass die Lösung in Spline-Form vorliegt, um einen glatten Plot zu erzeugen.

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot_a = res_a.sol(x_plot)[0]
>>> y_plot_b = res_b.sol(x_plot)[0]
>>> import matplotlib.pyplot as plt
>>> plt.plot(x_plot, y_plot_a, label='y_a')
>>> plt.plot(x_plot, y_plot_b, label='y_b')
>>> plt.legend()
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()

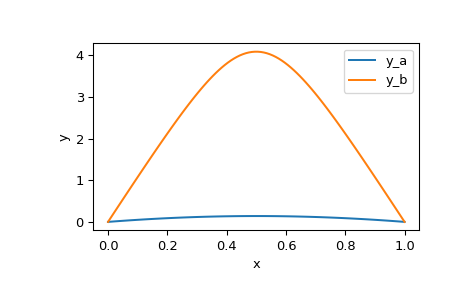
../../_images/scipy-integrate-solve_bvp-1_00_00.png

Wir sehen, dass die beiden Lösungen ähnliche Formen haben, sich aber in der Skalierung erheblich unterscheiden.

Im zweiten Beispiel lösen wir ein einfaches Sturm-Liouville-Problem

y'' + k**2 * y = 0
y(0) = y(1) = 0

Es ist bekannt, dass eine nicht-triviale Lösung y = A * sin(k * x) für k = pi * n, wobei n eine ganze Zahl ist, möglich ist. Um die Normierungskonstante A = 1 zu etablieren, fügen wir eine Randbedingung hinzu:

y'(0) = k

Auch hier schreiben wir unsere Gleichung als System erster Ordnung um und implementieren die Auswertung ihrer rechten Seite.

y1' = y2
y2' = -k**2 * y1

>>> def fun(x, y, p):
...     k = p[0]
...     return np.vstack((y[1], -k**2 * y[0]))

Beachten Sie, dass die Parameter p als Vektor (in unserem Fall mit einem Element) übergeben werden.

Implementieren Sie die Randbedingungen.

>>> def bc(ya, yb, p):
...     k = p[0]
...     return np.array([ya[0], yb[0], ya[1] - k])

Richten Sie das anfängliche Gitter und die Schätzung für y ein. Wir zielen darauf ab, die Lösung für k = 2 * pi zu finden. Um dies zu erreichen, setzen wir die Werte von y so, dass sie ungefähr sin(2 * pi * x) folgen.

>>> x = np.linspace(0, 1, 5)
>>> y = np.zeros((2, x.size))
>>> y[0, 1] = 1
>>> y[0, 3] = -1

Führen Sie den Solver mit 6 als anfänglicher Schätzung für k aus.

>>> sol = solve_bvp(fun, bc, x, y, p=[6])

Wir sehen, dass das gefundene k annähernd korrekt ist.

>>> sol.p[0]
6.28329460046

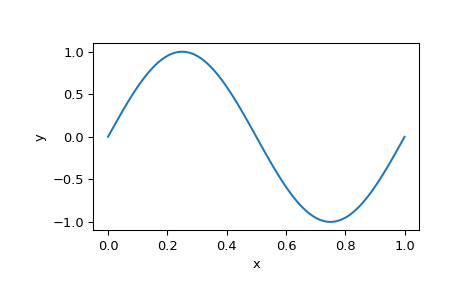
Und schließlich plotten wir die Lösung, um die erwartete Sinusoide zu sehen.

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot = sol.sol(x_plot)[0]
>>> plt.plot(x_plot, y_plot)
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()

../../_images/scipy-integrate-solve_bvp-1_01_00.png