AAA#
- class scipy.interpolate.AAA(x, y, *, rtol=None, max_terms=100, clean_up=True, clean_up_tol=1e-13)[Quelle]#
AAA reelle oder komplexe rationale Approximation.
Wie in [1] beschrieben, ist der AAA-Algorithmus ein Greedy-Algorithmus zur Approximation durch rationale Funktionen auf einer reellen oder komplexen Menge von Punkten. Die rationale Approximation wird in baryzentrischer Form dargestellt, aus der die Nullstellen (Nullen), Pole und Residuen berechnet werden können.
- Parameter:
- x1D array_like, shape (n,)
1D-Array mit den Werten der unabhängigen Variable. Werte können reell oder komplex sein, müssen aber endlich sein.
- y1D array_like, shape (n,)
Funktionswerte
f(x). Unendliche und NaN-Werte von values und entsprechende Werte von points werden verworfen.- rtolfloat, optional
Relative Toleranz, Standardwert ist
eps**0.75. Wenn ein kleiner Teil der Einträge in values viel größer ist als die restlichen, kann die Standardtoleranz zu locker sein. Wenn die Toleranz zu eng ist, kann die Approximation Froissart-Dubletten enthalten oder der Algorithmus konvergiert nicht mehr.- max_termsint, optional
Maximale Anzahl von Termen in der baryzentrischen Darstellung, Standardwert ist
100. Muss größer oder gleich eins sein.- clean_upbool, optional
Automatische Entfernung von Froissart-Dubletten, Standardwert ist
True. Siehe Hinweise für weitere Details.- clean_up_tolfloat, optional
Pole mit Residuen, die kleiner sind als diese Zahl multipliziert mit dem geometrischen Mittel von values multipliziert mit dem minimalen Abstand zu points, werden von der Bereinigungsroutine als spuriös betrachtet, Standardwert ist 1e-13. Siehe Hinweise für weitere Details.
- Attribute:
- support_pointsarray
Stützpunkte der Approximation. Dies ist eine Teilmenge der bereitgestellten x, an denen die Approximation y exakt interpoliert. Siehe Hinweise für weitere Details.
- support_valuesarray
Wert der Approximation an den
support_points.- weightsarray
Gewichte der baryzentrischen Approximation.
- errorsarray
Fehler \(|f(z) - r(z)|_\infty\) über points in den aufeinanderfolgenden Iterationen von AAA.
Methoden
__call__(z)Evaluiert die rationale Approximation an gegebenen Werten.
clean_up([cleanup_tol])Automatische Entfernung von Froissart-Dubletten.
poles()Berechnet die Pole der rationalen Approximation.
residues()Berechnet die Residuen der Pole der Approximation.
roots()Berechnet die Nullstellen der rationalen Approximation.
- Warnungen:
- RuntimeWarning
Wenn rtol in max_terms Iterationen nicht erreicht wird.
Siehe auch
FloaterHormannInterpolatorFloater-Hormann baryzentrische rationale Interpolation.
padePadé-Approximation.
Hinweise
In der Iteration \(m\) (an dem Punkt, an dem es \(m\) Terme sowohl im Zähler als auch im Nenner der Approximation gibt) nimmt die rationale Approximation im AAA-Algorithmus die baryzentrische Form an
\[r(z) = n(z)/d(z) = \frac{\sum_{j=1}^m\ w_j f_j / (z - z_j)}{\sum_{j=1}^m w_j / (z - z_j)},\]wobei \(z_1,\dots,z_m\) reelle oder komplexe Stützpunkte sind, die aus x ausgewählt wurden, \(f_1,\dots,f_m\) die entsprechenden reellen oder komplexen Datenwerte aus y sind und \(w_1,\dots,w_m\) reelle oder komplexe Gewichte sind.
Jede Iteration des Algorithmus besteht aus zwei Teilen: der gierigen Auswahl des nächsten Stützpunktes und der Berechnung der Gewichte. Der erste Teil jeder Iteration ist die Auswahl des nächsten hinzuzufügenden Stützpunktes \(z_{m+1}\) aus den verbleibenden nicht ausgewählten x, so dass der nichtlineare Rest \(|f(z_{m+1}) - n(z_{m+1})/d(z_{m+1})|\) maximiert wird. Der Algorithmus bricht ab, wenn dieser Maximalwert kleiner ist als
rtol * np.linalg.norm(f, ord=np.inf). Das bedeutet, dass die Interpolationseigenschaft nur bis zu einer Toleranz erfüllt ist, außer an den Stützpunkten, an denen die Approximation die bereitgestellten Daten exakt interpoliert.Im zweiten Teil jeder Iteration werden die Gewichte \(w_j\) ausgewählt, um das lineare Kleinste-Quadrate-Problem zu lösen
\[\text{minimise}_{w_j}|fd - n| \quad \text{unter der Bedingung} \quad \sum_{j=1}^{m+1} w_j = 1,\]über die nicht ausgewählten Elemente von x.
Eine der Herausforderungen bei der Arbeit mit rationalen Approximationen ist das Vorhandensein von Froissart-Dubletten, die entweder Pole mit verschwindend kleinen Residuen oder Pole-Nullstellen-Paare sind, die nahe genug beieinander liegen, um sich fast aufzuheben. Siehe [2]. Die gierige Natur des AAA-Algorithmus bedeutet, dass Froissart-Dubletten selten sind. Wenn jedoch rtol zu eng eingestellt ist, stagniert die Approximation und viele Froissart-Dubletten treten auf. Froissart-Dubletten können normalerweise entfernt werden, indem man Stützpunkte entfernt und dann das Kleinste-Quadrate-Problem neu löst. Der Stützpunkt \(z_j\), der dem Pol \(a\) mit Residuum \(\alpha\) am nächsten liegt, wird entfernt, wenn Folgendes erfüllt ist
\[|\alpha| / |z_j - a| < \verb|clean_up_tol| \cdot \tilde{f},\]wobei \(\tilde{f}\) das geometrische Mittel der
support_valuesist.Referenzen
[1] (1,2,3)Y. Nakatsukasa, O. Sete und L. N. Trefethen, „The AAA algorithm for rational approximation“, SIAM J. Sci. Comp. 40 (2018), A1494-A1522. DOI:10.1137/16M1106122
[2]J. Gilewicz und M. Pindor, Pade approximants and noise: rational functions, J. Comp. Appl. Math. 105 (1999), S. 285-297. DOI:10.1016/S0377-0427(02)00674-X
Beispiele
Hier reproduzieren wir einige der numerischen Beispiele aus [1] als Demonstration der Funktionalität dieser Methode.
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import AAA >>> import warnings
Für das erste Beispiel approximieren wir die Gammafunktion auf
[-3.5, 4.5], indem wir von 100 Stichproben in[-1.5, 1.5]extrapolieren.>>> from scipy.special import gamma >>> sample_points = np.linspace(-1.5, 1.5, num=100) >>> r = AAA(sample_points, gamma(sample_points)) >>> z = np.linspace(-3.5, 4.5, num=1000) >>> fig, ax = plt.subplots() >>> ax.plot(z, gamma(z), label="Gamma") >>> ax.plot(sample_points, gamma(sample_points), label="Sample points") >>> ax.plot(z, r(z).real, '--', label="AAA approximation") >>> ax.set(xlabel="z", ylabel="r(z)", ylim=[-8, 8], xlim=[-3.5, 4.5]) >>> ax.legend() >>> plt.show()
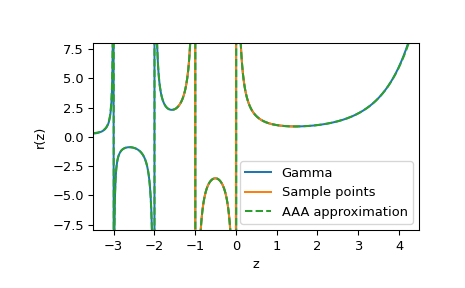
Wir können auch die Pole der rationalen Approximation und ihre Residuen betrachten.
>>> order = np.argsort(r.poles()) >>> r.poles()[order] array([-3.81591039e+00+0.j , -3.00269049e+00+0.j , -1.99999988e+00+0.j , -1.00000000e+00+0.j , 5.85842812e-17+0.j , 4.77485458e+00-3.06919376j, 4.77485458e+00+3.06919376j, 5.29095868e+00-0.97373072j, 5.29095868e+00+0.97373072j]) >>> r.residues()[order] array([ 0.03658074 +0.j , -0.16915426 -0.j , 0.49999915 +0.j , -1. +0.j , 1. +0.j , -0.81132013 -2.30193429j, -0.81132013 +2.30193429j, 0.87326839+10.70148546j, 0.87326839-10.70148546j])
Für das zweite Beispiel rufen wir
AAAmit einer Spirale von 1000 Punkten auf, die sich 7,5 Mal um den Ursprung in der komplexen Ebene windet.>>> z = np.exp(np.linspace(-0.5, 0.5 + 15j*np.pi, 1000)) >>> r = AAA(z, np.tan(np.pi*z/2), rtol=1e-13)
Wir sehen, dass AAA 12 Schritte zur Konvergenz benötigt mit den folgenden Fehlern
>>> r.errors.size 12 >>> r.errors array([2.49261500e+01, 4.28045609e+01, 1.71346935e+01, 8.65055336e-02, 1.27106444e-02, 9.90889874e-04, 5.86910543e-05, 1.28735561e-06, 3.57007424e-08, 6.37007837e-10, 1.67103357e-11, 1.17112299e-13])
Wir können auch die berechneten Pole plotten.
>>> fig, ax = plt.subplots() >>> ax.plot(z.real, z.imag, '.', markersize=2, label="Sample points") >>> ax.plot(r.poles().real, r.poles().imag, '.', markersize=5, ... label="Computed poles") >>> ax.set(xlim=[-3.5, 3.5], ylim=[-3.5, 3.5], aspect="equal") >>> ax.legend() >>> plt.show()
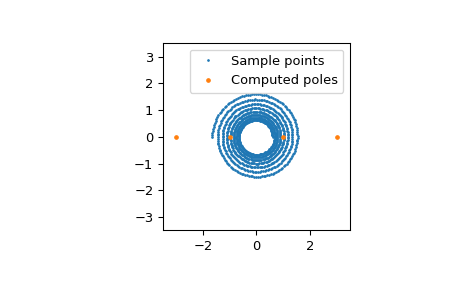
Wir demonstrieren nun die Entfernung von Froissart-Dubletten mithilfe der Methode
clean_upanhand eines Beispiels aus [1]. Hier approximieren wir die Funktion \(f(z)=\log(2 + z^4)/(1 + 16z^4)\), indem wir sie an 1000 Einheitswurzeln abtasten. Der Algorithmus wird mitrtol=0undclean_up=Falseausgeführt, um absichtlich Froissart-Dubletten zu erzeugen.>>> z = np.exp(1j*2*np.pi*np.linspace(0,1, num=1000)) >>> def f(z): ... return np.log(2 + z**4)/(1 - 16*z**4) >>> with warnings.catch_warnings(): # filter convergence warning due to rtol=0 ... warnings.simplefilter('ignore', RuntimeWarning) ... r = AAA(z, f(z), rtol=0, max_terms=50, clean_up=False) >>> mask = np.abs(r.residues()) < 1e-13 >>> fig, axs = plt.subplots(ncols=2) >>> axs[0].plot(r.poles().real[~mask], r.poles().imag[~mask], '.') >>> axs[0].plot(r.poles().real[mask], r.poles().imag[mask], 'r.')
Nun rufen wir die Methode
clean_upauf, um Froissart-Dubletten zu entfernen.>>> with warnings.catch_warnings(): ... warnings.simplefilter('ignore', RuntimeWarning) ... r.clean_up() 4 # may vary >>> mask = np.abs(r.residues()) < 1e-13 >>> axs[1].plot(r.poles().real[~mask], r.poles().imag[~mask], '.') >>> axs[1].plot(r.poles().real[mask], r.poles().imag[mask], 'r.') >>> plt.show()
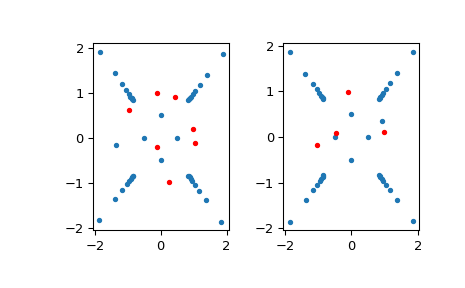
Das linke Bild zeigt die Pole vor der Approximation mit
clean_up=False, wobei Pole mit einem Residuum kleiner als10^-13im Absolutwert rot dargestellt sind. Das rechte Bild zeigt dann die Pole nach dem Aufruf der Methodeclean_up.