scipy.interpolate.

BSpline#

class scipy.interpolate.BSpline(t, c, k, extrapolate=True, axis=0)[Quelle]#

Univariate Spline in der B-Spline-Basis.

\[S(x) = \sum_{j=0}^{n-1} c_j B_{j, k; t}(x)\]

wobei $B_{j, k; t}$ B-Spline-Basisfunktionen vom Grad k und den Knoten t sind.

Parameter:

tndarray, Form (n+k+1,): Knoten
cndarray, Form (>=n, …): Spline-Koeffizienten
kint: B-Spline-Grad
extrapolatebool oder ‘periodic’, optional: ob über das Basisintervall, t[k] .. t[n], hinaus extrapoliert werden soll oder NaNs zurückgegeben werden sollen. Wenn True, werden die erste und letzte Polynomteile der B-Spline-Funktionen, die im Basisintervall aktiv sind, extrapoliert. Wenn 'periodic', wird eine periodische Extrapolation verwendet. Standard ist True.
axisint, optional: Interpolationsachse. Standard ist Null.

Attribute:

tndarray: Knotenvektor
cndarray: Spline-Koeffizienten
kint: Spline-Grad
extrapolatebool: Wenn True, werden die erste und letzte Polynomteile der B-Spline-Funktionen, die im Basisintervall aktiv sind, extrapoliert.
axisint: Interpolationsachse.
tcktuple: Äquivalent zu (self.t, self.c, self.k) (nur lesbar).

Methoden

`__call__`(x[, nu, extrapolate])	Eine Spline-Funktion auswerten.
`basis_element`(t[, extrapolate])	Gibt ein B-Spline-Basiselement `B(x \| t[0], ..., t[k+1])` zurück.
`derivative`([nu])	Gibt einen B-Spline zurück, der die Ableitung repräsentiert.
`antiderivative`([nu])	Gibt einen B-Spline zurück, der die Stammfunktion repräsentiert.
`integrate`(a, b[, extrapolate])	Berechnet ein bestimmtes Integral des Splines.
`insert_knot`(x[, m])	Fügt einen neuen Knoten bei x mit der Vielfachheit m ein.
`construct_fast`(t, c, k[, extrapolate, axis])	Konstruiert einen Spline ohne Überprüfungen.
`design_matrix`(x, t, k[, extrapolate])	Gibt eine Designmatrix als spärliches Array im CSR-Format zurück.
`from_power_basis`(pp[, bc_type])	Konstruiert ein Polynom in der B-Spline-Basis aus einem stückweisen Polynom in der Potenzbasis.

Hinweise

B-Spline-Basiselemente sind definiert über

\[ \begin{align}\begin{aligned}B_{i, 0}(x) = 1, \textrm{wenn $t_i \le x < t_{i+1}$, sonst $0$,}\\B_{i, k}(x) = \frac{x - t_i}{t_{i+k} - t_i} B_{i, k-1}(x) + \frac{t_{i+k+1} - x}{t_{i+k+1} - t_{i+1}} B_{i+1, k-1}(x)\end{aligned}\end{align} \]

Implementierungsdetails

Für einen Spline vom Grad k sind mindestens k+1 Koeffizienten erforderlich, so dass n >= k+1 gilt. Zusätzliche Koeffizienten, c[j] mit j > n, werden ignoriert.
B-Spline-Basiselemente vom Grad k bilden eine Partition der Eins über das Basisintervall, t[k] <= x <= t[n].

Referenzen

[1]

Tom Lyche und Knut Morken, Spline methods, http://www.uio.no/studier/emner/matnat/ifi/INF-MAT5340/v05/undervisningsmateriale/

[2]

Carl de Boor, A practical guide to splines, Springer, 2001.

Beispiele

Wenn wir die rekursive Definition von B-Splines in Python-Code übersetzen, erhalten wir

>>> def B(x, k, i, t):
...    if k == 0:
...       return 1.0 if t[i] <= x < t[i+1] else 0.0
...    if t[i+k] == t[i]:
...       c1 = 0.0
...    else:
...       c1 = (x - t[i])/(t[i+k] - t[i]) * B(x, k-1, i, t)
...    if t[i+k+1] == t[i+1]:
...       c2 = 0.0
...    else:
...       c2 = (t[i+k+1] - x)/(t[i+k+1] - t[i+1]) * B(x, k-1, i+1, t)
...    return c1 + c2

>>> def bspline(x, t, c, k):
...    n = len(t) - k - 1
...    assert (n >= k+1) and (len(c) >= n)
...    return sum(c[i] * B(x, k, i, t) for i in range(n))

Beachten Sie, dass dies eine ineffiziente (wenn auch einfache) Methode zur Auswertung von B-Splines ist — diese Spline-Klasse tut dies auf eine äquivalente, aber wesentlich effizientere Weise.

Hier konstruieren wir eine quadratische Spline-Funktion auf dem Basisintervall 2 <= x <= 4 und vergleichen sie mit der naiven Art, den Spline auszuwerten

>>> from scipy.interpolate import BSpline
>>> k = 2
>>> t = [0, 1, 2, 3, 4, 5, 6]
>>> c = [-1, 2, 0, -1]
>>> spl = BSpline(t, c, k)
>>> spl(2.5)
array(1.375)
>>> bspline(2.5, t, c, k)
1.375

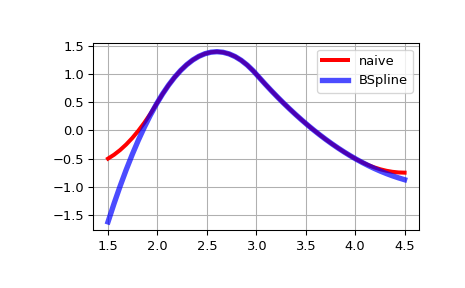
Beachten Sie, dass die Ergebnisse außerhalb des Basisintervalls unterschiedlich sind. Dies liegt daran, dass BSpline die erste und letzte Polynomteile der B-Spline-Funktionen, die im Basisintervall aktiv sind, extrapoliert.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> fig, ax = plt.subplots()
>>> xx = np.linspace(1.5, 4.5, 50)
>>> ax.plot(xx, [bspline(x, t, c ,k) for x in xx], 'r-', lw=3, label='naive')
>>> ax.plot(xx, spl(xx), 'b-', lw=4, alpha=0.7, label='BSpline')
>>> ax.grid(True)
>>> ax.legend(loc='best')
>>> plt.show()

../../_images/scipy-interpolate-BSpline-1.png