scipy.interpolate.LSQSphereBivariateSpline.

call#

LSQSphereBivariateSpline.__call__(theta, phi, dtheta=0, dphi=0, grid=True)[source]#

Evaluieren des Splines oder seiner Ableitungen an gegebenen Positionen.

Parameter:

theta, phiarray_like

Eingabekoordinaten.

Wenn grid falsch ist, werten Sie die Spline an den Punkten (theta[i], phi[i]), i=0, ..., len(x)-1 aus. Die Standard-Numpy-Broadcasting-Regeln werden befolgt.

Wenn grid wahr ist: Werten Sie die Spline an den durch die Koordinatenarrays theta, phi definierten Gitterpunkten aus. Die Arrays müssen sortiert aufsteigend sein. Die Reihenfolge der Achsen ist konsistent mit np.meshgrid(..., indexing="ij") und inkonsistent mit der Standardreihenfolge np.meshgrid(..., indexing="xy").

dthetaint, optional

Ordnung der Theta-Ableitung

Hinzugefügt in Version 0.14.0.

dphiint

Ordnung der Phi-Ableitung

Hinzugefügt in Version 0.14.0.

gridbool

Ob die Ergebnisse auf einem Gitter, das von den Eingabearrays aufgespannt wird, oder an Punkten, die durch die Eingabearrays spezifiziert werden, ausgewertet werden sollen.

Hinzugefügt in Version 0.14.0.

Beispiele

Angenommen, wir möchten Splines verwenden, um eine bivariate Funktion auf einer Kugel zu interpolieren. Der Wert der Funktion ist auf einem Gitter von Längen- und Kolatituden bekannt.

>>> import numpy as np
>>> from scipy.interpolate import RectSphereBivariateSpline
>>> def f(theta, phi):
...     return np.sin(theta) * np.cos(phi)

Wir werten die Funktion auf dem Gitter aus. Beachten Sie, dass die Standard-Indexing=”xy” von meshgrid nach der Interpolation ein unerwartetes (transponiertes) Ergebnis liefern würde.

>>> thetaarr = np.linspace(0, np.pi, 22)[1:-1]
>>> phiarr = np.linspace(0, 2 * np.pi, 21)[:-1]
>>> thetagrid, phigrid = np.meshgrid(thetaarr, phiarr, indexing="ij")
>>> zdata = f(thetagrid, phigrid)

Wir richten nun den Interpolator ein und verwenden ihn, um die Funktion auf einem feineren Gitter auszuwerten.

>>> rsbs = RectSphereBivariateSpline(thetaarr, phiarr, zdata)
>>> thetaarr_fine = np.linspace(0, np.pi, 200)
>>> phiarr_fine = np.linspace(0, 2 * np.pi, 200)
>>> zdata_fine = rsbs(thetaarr_fine, phiarr_fine)

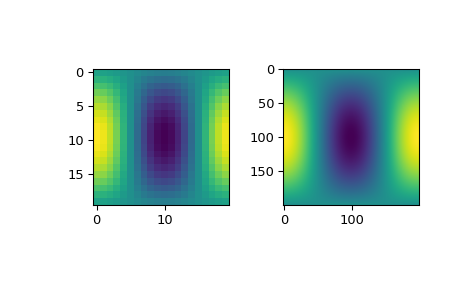
Schließlich plotten wir die grob abgetasteten Eingabedaten neben den fein abgetasteten interpolierten Daten, um zu überprüfen, ob sie übereinstimmen.

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(1, 2, 1)
>>> ax2 = fig.add_subplot(1, 2, 2)
>>> ax1.imshow(zdata)
>>> ax2.imshow(zdata_fine)
>>> plt.show()

../../_images/scipy-interpolate-LSQSphereBivariateSpline-__call__-1.png

__call__#

call#