RBFInterpolator#
- class scipy.interpolate.RBFInterpolator(y, d, neighbors=None, smoothing=0.0, kernel='thin_plate_spline', epsilon=None, degree=None)[Quelle]#
Radial Basis Function (RBF) Interpolator in N ≥ 1 Dimensionen.
- Parameter:
- y(npoints, ndims) array_like
2-D Array von Koordinaten der Datenpunkte.
- d(npoints, …) array_like
N-D Array von Datenwerten bei y. Die Länge von d entlang der ersten Achse muss gleich der Länge von y sein. Im Gegensatz zu einigen Interpolatoren kann die Interpolationsachse nicht geändert werden.
- neighborsint, optional
Wenn angegeben, wird der Wert des Interpolanten an jedem Auswertungspunkt nur anhand dieser vielen nächstgelegenen Datenpunkte berechnet. Standardmäßig werden alle Datenpunkte verwendet.
- smoothingfloat oder (npoints, ) array_like, optional
Glättungsparameter. Der Interpolant passt sich den Daten perfekt an, wenn dieser auf 0 gesetzt ist. Für große Werte nähert sich der Interpolant einer kleinstquadratischen Anpassung eines Polynoms mit dem angegebenen Grad an. Standardwert ist 0.
- kernelstr, optional
Art der RBF. Dies sollte einer der folgenden sein:
‘linear’ :
-r‘thin_plate_spline’ :
r**2 * log(r)‘cubic’ :
r**3‘quintic’ :
-r**5‘multiquadric’ :
-sqrt(1 + r**2)‘inverse_multiquadric’ :
1/sqrt(1 + r**2)‘inverse_quadratic’ :
1/(1 + r**2)‘gaussian’ :
exp(-r**2)
Standardwert ist ‘thin_plate_spline’.
- epsilonfloat, optional
Formparameter, der die Eingabe für die RBF skaliert. Wenn kernel ‘linear’, ‘thin_plate_spline’, ‘cubic’ oder ‘quintic’ ist, ist dieser standardmäßig 1 und kann ignoriert werden, da er dieselbe Wirkung wie die Skalierung des Glättungsparameters hat. Andernfalls muss dieser angegeben werden.
- degreeint, optional
Grad des hinzugefügten Polynoms. Bei einigen RBFs ist der Interpolant möglicherweise nicht gut gestellt, wenn der Polynomgrad zu gering ist. Diese RBFs und ihre entsprechenden Mindestgrade sind:
‘multiquadric’ : 0
‘linear’ : 0
‘thin_plate_spline’ : 1
‘cubic’ : 1
‘quintic’ : 2
Der Standardwert ist der Mindestgrad für kernel oder 0, wenn kein Mindestgrad vorhanden ist. Setzen Sie diesen auf -1, um kein hinzugefügtes Polynom zu haben.
Methoden
__call__(x)Evaluiert den Interpolanten an x.
Hinweise
Eine RBF ist eine skalarwertige Funktion in einem N-dimensionalen Raum, deren Wert bei \(x\) ausgedrückt werden kann als Terme von \(r=||x - c||\), wobei \(c\) das Zentrum der RBF ist.
Ein RBF-Interpolant für den Vektor der Datenwerte \(d\), die von den Orten \(y\) stammen, ist eine lineare Kombination von RBFs mit Zentren bei \(y\) plus einem Polynom mit einem spezifizierten Grad. Der RBF-Interpolant wird wie folgt geschrieben:
\[f(x) = K(x, y) a + P(x) b,\]wobei \(K(x, y)\) eine Matrix von RBFs mit Zentren bei \(y\) ist, die an den Punkten \(x\) ausgewertet werden, und \(P(x)\) eine Matrix von Monomen ist, die Polynome mit dem spezifizierten Grad aufspannt und an \(x\) ausgewertet wird. Die Koeffizienten \(a\) und \(b\) sind die Lösung der linearen Gleichungen
\[(K(y, y) + \lambda I) a + P(y) b = d\]und
\[P(y)^T a = 0,\]wobei \(\lambda\) ein nicht-negativer Glättungsparameter ist, der steuert, wie gut wir die Daten anpassen wollen. Die Daten werden exakt angepasst, wenn der Glättungsparameter 0 ist.
Das obige System ist eindeutig lösbar, wenn die folgenden Anforderungen erfüllt sind:
\(P(y)\) muss vollen Spaltenrang haben. \(P(y)\) hat immer vollen Spaltenrang, wenn degree -1 oder 0 ist. Wenn degree 1 ist, hat \(P(y)\) vollen Spaltenrang, wenn die Datenpunktstandorte nicht alle kollinear (N=2), koplanar (N=3) usw. sind.
Wenn kernel ‘multiquadric’, ‘linear’, ‘thin_plate_spline’, ‘cubic’ oder ‘quintic’ ist, darf degree nicht kleiner sein als der oben aufgeführte Mindestwert.
Wenn smoothing 0 ist, muss jeder Datenpunktstandort eindeutig sein.
Bei Verwendung einer RBF, die nicht skaleninvariant ist (‘multiquadric’, ‘inverse_multiquadric’, ‘inverse_quadratic’ oder ‘gaussian’), muss ein geeigneter Formparameter gewählt werden (z. B. durch Kreuzvalidierung). Kleinere Werte für den Formparameter entsprechen breiteren RBFs. Das Problem kann schlecht konditioniert oder singulär werden, wenn der Formparameter zu klein ist.
Der Speicherbedarf zur Lösung der RBF-Interpolationskoeffizienten steigt quadratisch mit der Anzahl der Datenpunkte an, was bei der Interpolation von mehr als etwa tausend Datenpunkten unpraktisch werden kann. Um Speicherbeschränkungen für große Interpolationsprobleme zu überwinden, kann das Argument neighbors angegeben werden, um für jeden Auswertungspunkt einen RBF-Interpolanten unter Verwendung nur der nächstgelegenen Datenpunkte zu berechnen.
Hinzugefügt in Version 1.7.0.
Referenzen
[1]Fasshauer, G., 2007. Meshfree Approximation Methods with Matlab. World Scientific Publishing Co.
[3]Wahba, G., 1990. Spline Models for Observational Data. SIAM.
Beispiele
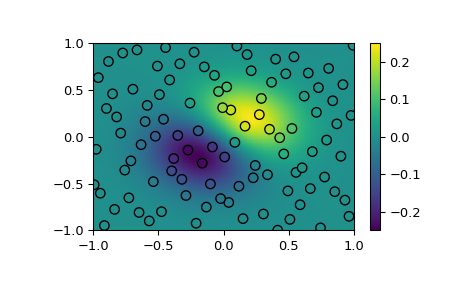
Demonstriert die Interpolation von gestreuten Daten auf ein Gitter in 2-D.
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import RBFInterpolator >>> from scipy.stats.qmc import Halton
>>> rng = np.random.default_rng() >>> xobs = 2*Halton(2, seed=rng).random(100) - 1 >>> yobs = np.sum(xobs, axis=1)*np.exp(-6*np.sum(xobs**2, axis=1))
>>> xgrid = np.mgrid[-1:1:50j, -1:1:50j] >>> xflat = xgrid.reshape(2, -1).T >>> yflat = RBFInterpolator(xobs, yobs)(xflat) >>> ygrid = yflat.reshape(50, 50)
>>> fig, ax = plt.subplots() >>> ax.pcolormesh(*xgrid, ygrid, vmin=-0.25, vmax=0.25, shading='gouraud') >>> p = ax.scatter(*xobs.T, c=yobs, s=50, ec='k', vmin=-0.25, vmax=0.25) >>> fig.colorbar(p) >>> plt.show()