scipy.linalg.

lstsq#

scipy.linalg.lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)[Quelle]#

Berechnet die Kleinste-Quadrate-Lösung der Gleichung a @ x = b.

Berechnet einen Vektor x, so dass die 2-Norm |b - A x| minimiert wird.

Die Dokumentation wurde unter der Annahme verfasst, dass die Array-Argumente bestimmte „Kern“-Formen haben. Array-Argumente dieser Funktion können jedoch zusätzliche „Batch“-Dimensionen vorangestellt haben. In diesem Fall wird das Array als Stapel von niedrigdimensionalen Schnitten behandelt; siehe Gestapelte lineare Operationen für Details.

Parameter:

a(M, N) array_like: Array der linken Seite
b(M,) oder (M, K) array_like: Array der rechten Seite
condfloat, optional: Schwellenwert für „kleine“ Singulärwerte; wird zur Bestimmung des effektiven Rangs von a verwendet. Singulärwerte, die kleiner sind als cond * größter_singulärwert, werden als Null betrachtet.
overwrite_abool, optional: Verwirft Daten in a (kann die Leistung verbessern). Standard ist False.
overwrite_bbool, optional: Verwirft Daten in b (kann die Leistung verbessern). Standard ist False.
check_finitebool, optional: Ob überprüft werden soll, ob die Eingabematrizen nur endliche Zahlen enthalten. Das Deaktivieren kann zu einer Leistungssteigerung führen, kann aber zu Problemen (Abstürzen, Nicht-Terminierung) führen, wenn die Eingaben Unendlichkeiten oder NaNs enthalten.
lapack_driverstr, optional: Welcher LAPACK-Treiber zur Lösung des Kleinste-Quadrate-Problems verwendet wird. Optionen sind 'gelsd', 'gelsy', 'gelss'. Die Standardeinstellung ('gelsd') ist eine gute Wahl. 'gelsy' kann jedoch bei vielen Problemen etwas schneller sein. 'gelss' wurde historisch verwendet. Es ist im Allgemeinen langsam, verbraucht aber weniger Speicher.

Hinzugefügt in Version 0.17.0.

Rückgabe:

x(N,) oder (N, K) ndarray: Kleinste-Quadrate-Lösung.
residues(K,) ndarray oder float: Quadrat der 2-Norm für jede Spalte in b - a x, wenn M > N und rank(A) == n (gibt einen Skalar zurück, wenn b 1-dimensional ist). Andernfalls wird ein Array der Form (0,) zurückgegeben.
rankint: Effektiver Rang von a.
s(min(M, N),) ndarray oder None: Singulärwerte von a. Die Konditionszahl von a ist s[0] / s[-1].

Löst aus:

LinAlgError: Wenn die Berechnung nicht konvergiert.
ValueError: Wenn Parameter nicht kompatibel sind.

Siehe auch

scipy.optimize.nnls: lineare Kleinste-Quadrate-Anpassung mit Nicht-Negativitäts-Beschränkung

Hinweise

Wenn 'gelsy' als Treiber verwendet wird, wird residues auf ein Array der Form (0,) gesetzt und s ist immer None.

Beispiele

>>> import numpy as np
>>> from scipy.linalg import lstsq
>>> import matplotlib.pyplot as plt

Angenommen, wir haben die folgenden Daten

>>> x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5])
>>> y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])

Wir möchten ein quadratisches Polynom der Form y = a + b*x**2 an diese Daten anpassen. Wir bilden zuerst die „Designmatrix“ M, mit einer konstanten Spalte von 1en und einer Spalte, die x**2 enthält

>>> M = x[:, np.newaxis]**[0, 2]
>>> M
array([[  1.  ,   1.  ],
       [  1.  ,   6.25],
       [  1.  ,  12.25],
       [  1.  ,  16.  ],
       [  1.  ,  25.  ],
       [  1.  ,  49.  ],
       [  1.  ,  72.25]])

Wir möchten die Kleinste-Quadrate-Lösung für M.dot(p) = y finden, wobei p ein Vektor der Länge 2 ist, der die Parameter a und b enthält.

>>> p, res, rnk, s = lstsq(M, y)
>>> p
array([ 0.20925829,  0.12013861])

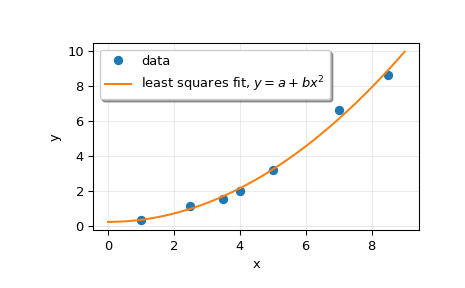
Zeichnen Sie die Daten und die angepasste Kurve.

>>> plt.plot(x, y, 'o', label='data')
>>> xx = np.linspace(0, 9, 101)
>>> yy = p[0] + p[1]*xx**2
>>> plt.plot(xx, yy, label='least squares fit, $y = a + bx^2$')
>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.grid(alpha=0.25)
>>> plt.show()