scipy.optimize.

root#

scipy.optimize.root(fun, x0, args=(), method='hybr', jac=None, tol=None, callback=None, options=None)[Quelle]#

Finde eine Wurzel einer Vektorfunktion.

Parameter:

funcallable

Eine Vektorfunktion, für die eine Wurzel gesucht werden soll.

Angenommen, die aufrufbare Funktion hat die Signatur f0(x, *my_args, **my_kwargs), wobei my_args und my_kwargs erforderliche Positions- und Schlüsselwortargumente sind. Anstatt f0 als aufrufbare Funktion zu übergeben, wickeln Sie sie so ein, dass sie nur x akzeptiert; z. B. übergeben Sie fun=lambda x: f0(x, *my_args, **my_kwargs) als aufrufbare Funktion, wobei my_args (Tupel) und my_kwargs (Dict) vor dem Aufruf dieser Funktion gesammelt wurden.

x0ndarray

Anfangsschätzung.

argstuple, optional

Zusätzliche Argumente, die an die Zielfunktion und ihre Jacobi-Matrix übergeben werden.

methodstr, optional

Art des Lösers. Muss eine der folgenden sein:

„hybr“ (siehe hier)
„lm“ (siehe hier)
„broyden1“ (siehe hier)
„broyden2“ (siehe hier)
„anderson“ (siehe hier)
„linearmixing“ (siehe hier)
„diagbroyden“ (siehe hier)
„excitingmixing“ (siehe hier)
„krylov“ (siehe hier)
„df-sane“ (siehe hier)

jacbool oder callable, optional

Wenn jac ein Boolean ist und True ist, wird angenommen, dass fun den Wert der Jacobi-Matrix zusammen mit der Zielfunktion zurückgibt. Wenn False, wird die Jacobi-Matrix numerisch geschätzt. jac kann auch eine aufrufbare Funktion sein, die die Jacobi-Matrix von fun zurückgibt. In diesem Fall muss sie dieselben Argumente wie fun akzeptieren.

tolfloat, optional

Toleranz für die Beendigung. Für detaillierte Steuerung verwenden Sie Solver-spezifische Optionen.

callbackfunction, optional

Optionale Callback-Funktion. Sie wird bei jeder Iteration als callback(x, f) aufgerufen, wobei x die aktuelle Lösung und f der entsprechende Rest ist. Für alle Methoden außer ‚hybr‘ und ‚lm‘.

optionsdict, optional

Ein Dictionary von Solver-Optionen. Z. B. xtol oder maxiter, siehe show_options() für Details.

Rückgabe:

solOptimizeResult: Die Lösung, dargestellt als ein OptimizeResult-Objekt. Wichtige Attribute sind: x das Lösungsarray, success ein Boolean-Flag, das angibt, ob der Algorithmus erfolgreich beendet wurde, und message, das den Grund für die Beendigung beschreibt. Siehe OptimizeResult für eine Beschreibung anderer Attribute.

Siehe auch

show_options: Zusätzliche Optionen, die von den Lösungsalgorithmen akzeptiert werden

Hinweise

Dieser Abschnitt beschreibt die verfügbaren Lösungsalgorithmen, die mit dem Parameter ‚method‘ ausgewählt werden können. Die Standardmethode ist hybr.

Die Methode hybr verwendet eine Modifikation der Powell-Hybrid-Methode, wie sie in MINPACK implementiert ist [1].

Die Methode lm löst das System nichtlinearer Gleichungen im Sinne der kleinsten Quadrate unter Verwendung einer Modifikation des Levenberg-Marquardt-Algorithmus, wie er in MINPACK implementiert ist [1].

Die Methode df-sane ist eine ableitungsfreie spektrale Methode. [3]

Die Methoden broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov sind inexakte Newton-Methoden mit Backtracking oder vollständiger Liniensuche [2]. Jede Methode entspricht einer bestimmten Jacobi-Matrix-Approximation.

Die Methode broyden1 verwendet Broydens erste Jacobi-Matrix-Approximation, sie ist bekannt als Broydens gute Methode.
Die Methode broyden2 verwendet Broydens zweite Jacobi-Matrix-Approximation, sie ist bekannt als Broydens schlechte Methode.
Die Methode anderson verwendet (erweiterte) Anderson-Mischung.
Die Methode Krylov verwendet Krylov-Approximation für die inverse Jacobi-Matrix. Sie ist für große Probleme geeignet.
Die Methode diagbroyden verwendet eine diagonale Broyden-Jacobi-Matrix-Approximation.
Die Methode linearmixing verwendet eine skalare Jacobi-Matrix-Approximation.
Die Methode excitingmixing verwendet eine abgestimmte diagonale Jacobi-Matrix-Approximation.

Warnung

Die für die Methoden diagbroyden, linearmixing und excitingmixing implementierten Algorithmen können für spezifische Probleme nützlich sein, aber ob sie funktionieren, hängt stark vom Problem ab.

Hinzugefügt in Version 0.11.0.

Referenzen

[1] (1,2)

More, Jorge J., Burton S. Garbow und Kenneth E. Hillstrom. 1980. User Guide for MINPACK-1.

[2]

C. T. Kelley. 1995. Iterative Methods for Linear and Nonlinear Equations. Society for Industrial and Applied Mathematics. <https://archive.siam.org/books/kelley/fr16/>

[3]

La Cruz, J.M. Martinez, M. Raydan. Math. Comp. 75, 1429 (2006).

Beispiele

Die folgenden Funktionen definieren ein System nichtlinearer Gleichungen und seine Jacobi-Matrix.

>>> import numpy as np
>>> def fun(x):
...     return [x[0]  + 0.5 * (x[0] - x[1])**3 - 1.0,
...             0.5 * (x[1] - x[0])**3 + x[1]]

>>> def jac(x):
...     return np.array([[1 + 1.5 * (x[0] - x[1])**2,
...                       -1.5 * (x[0] - x[1])**2],
...                      [-1.5 * (x[1] - x[0])**2,
...                       1 + 1.5 * (x[1] - x[0])**2]])

Eine Lösung kann wie folgt erzielt werden.

>>> from scipy import optimize
>>> sol = optimize.root(fun, [0, 0], jac=jac, method='hybr')
>>> sol.x
array([ 0.8411639,  0.1588361])

Großes Problem

Angenommen, wir müssten die folgende integrodifferentiale Gleichung auf dem Quadrat \([0,1]\times[0,1]\) lösen

\[\nabla^2 P = 10 \left(\int_0^1\int_0^1\cosh(P)\,dx\,dy\right)^2\]

mit \(P(x,1) = 1\) und \(P=0\) anderswo am Rand des Quadrats.

Die Lösung kann mit dem Lösungsalgorithmus method='krylov' gefunden werden

>>> from scipy import optimize
>>> # parameters
>>> nx, ny = 75, 75
>>> hx, hy = 1./(nx-1), 1./(ny-1)

>>> P_left, P_right = 0, 0
>>> P_top, P_bottom = 1, 0

>>> def residual(P):
...    d2x = np.zeros_like(P)
...    d2y = np.zeros_like(P)
...
...    d2x[1:-1] = (P[2:]   - 2*P[1:-1] + P[:-2]) / hx/hx
...    d2x[0]    = (P[1]    - 2*P[0]    + P_left)/hx/hx
...    d2x[-1]   = (P_right - 2*P[-1]   + P[-2])/hx/hx
...
...    d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
...    d2y[:,0]    = (P[:,1]  - 2*P[:,0]    + P_bottom)/hy/hy
...    d2y[:,-1]   = (P_top   - 2*P[:,-1]   + P[:,-2])/hy/hy
...
...    return d2x + d2y - 10*np.cosh(P).mean()**2

>>> guess = np.zeros((nx, ny), float)
>>> sol = optimize.root(residual, guess, method='krylov')
>>> print('Residual: %g' % abs(residual(sol.x)).max())
Residual: 5.7972e-06  # may vary

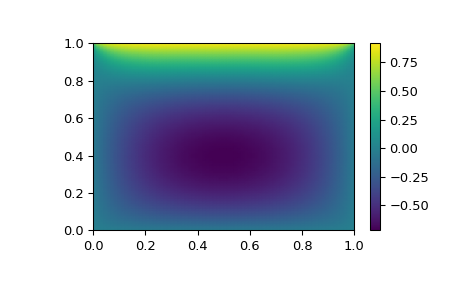
>>> import matplotlib.pyplot as plt
>>> x, y = np.mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
>>> plt.pcolormesh(x, y, sol.x, shading='gouraud')
>>> plt.colorbar()
>>> plt.show()