cheby1#
- scipy.signal.cheby1(N, rp, Wn, btype='low', analog=False, output='ba', fs=None)[Quelle]#
Entwurf eines digitalen oder analogen Chebyshev-Typs I-Filters.
Entwirft einen digitalen oder analogen Chebyshev-Typ-I-Filter der Ordnung N und gibt die Filterkoeffizienten zurück.
- Parameter:
- Nint
Die Ordnung des Filters.
- rpfloat
Die maximal zulässige Welligkeit unterhalb der Einheitsverstärkung im Durchlassbereich. Angegeben in Dezibel, als positive Zahl.
- Wnarray_like
Eine Skalar- oder Längen-2-Sequenz, die die Grenzfrequenzen angibt. Für Typ-I-Filter ist dies der Punkt im Übergangsbereich, an dem die Verstärkung erstmals unter -rp fällt.
Für digitale Filter sind Wn in derselben Einheit wie fs angegeben. Standardmäßig ist fs 2 Halbzyklen/Sample, daher sind diese von 0 bis 1 normalisiert, wobei 1 die Nyquist-Frequenz ist. (Wn sind somit in Halbzyklen / Sample.)
Für analoge Filter ist Wn eine Winkelfrequenz (z. B. rad/s).
- btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, optional
Der Filtertyp. Standard ist ‘lowpass’.
- analogbool, optional
Wenn True, wird ein analoger Filter zurückgegeben, andernfalls ein digitaler Filter.
- output{‘ba’, ‘zpk’, ‘sos’}, optional
Typ der Ausgabe: Zähler/Nenner („ba“), Pol-Nullstelle („zpk“) oder Sektionen zweiter Ordnung („sos“). Standard ist „ba“ aus Gründen der Abwärtskompatibilität, aber „sos“ sollte für allgemeine Filterung verwendet werden.
- fsfloat, optional
Die Abtastfrequenz des digitalen Systems.
Hinzugefügt in Version 1.2.0.
- Rückgabe:
- b, andarray, ndarray
Zähler- (b) und Nenner- (a) Polynome des IIR-Filters. Nur zurückgegeben, wenn
output='ba'.- z, p, kndarray, ndarray, float
Nullstellen, Pole und Systemverstärkung der Übertragungsfunktion des IIR-Filters. Nur zurückgegeben, wenn
output='zpk'.- sosndarray
Zweistufige Abschnittsdarstellung des IIR-Filters. Nur zurückgegeben, wenn
output='sos'.
Hinweise
Der Chebyshev-Typ-I-Filter maximiert die Anstiegsrate zwischen dem Durchlassbereich und dem Sperrbereich der Frequenzantwort, auf Kosten von Welligkeit im Durchlassbereich und erhöhter Schwingung in der Sprungantwort.
Typ-I-Filter haben einen schnelleren Abfall als Typ-II-Filter (
cheby2), aber Typ-II-Filter haben keine Welligkeit im Durchlassbereich.Der äquireplische Durchlassbereich hat N Maxima oder Minima (z. B. hat ein Filter 5. Ordnung 3 Maxima und 2 Minima). Folglich ist die DC-Verstärkung für Filter ungerader Ordnung eins, und für Filter gerader Ordnung -rp dB.
Der Parameter
output='sos'wurde in 0.16.0 hinzugefügt.Beispiele
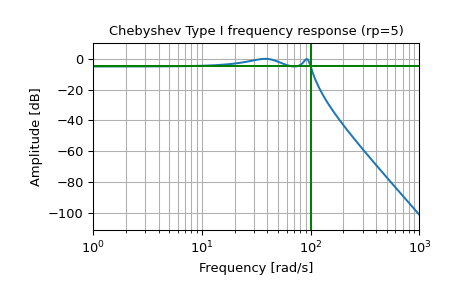
Entwurf eines analogen Filters und Darstellung seiner Frequenzgangkurve, wobei die kritischen Punkte gezeigt werden
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> import numpy as np
>>> b, a = signal.cheby1(4, 5, 100, 'low', analog=True) >>> w, h = signal.freqs(b, a) >>> plt.semilogx(w, 20 * np.log10(abs(h))) >>> plt.title('Chebyshev Type I frequency response (rp=5)') >>> plt.xlabel('Frequency [rad/s]') >>> plt.ylabel('Amplitude [dB]') >>> plt.margins(0, 0.1) >>> plt.grid(which='both', axis='both') >>> plt.axvline(100, color='green') # cutoff frequency >>> plt.axhline(-5, color='green') # rp >>> plt.show()
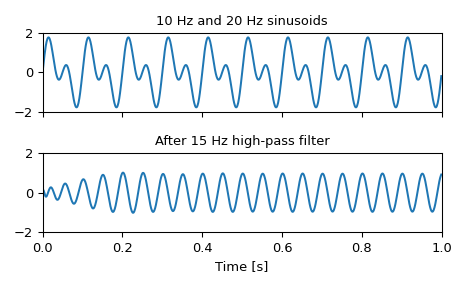
Generieren eines Signals, das aus 10 Hz und 20 Hz besteht, abgetastet mit 1 kHz
>>> t = np.linspace(0, 1, 1000, False) # 1 second >>> sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t) >>> fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True) >>> ax1.plot(t, sig) >>> ax1.set_title('10 Hz and 20 Hz sinusoids') >>> ax1.axis([0, 1, -2, 2])
Entwerfen Sie einen digitalen Hochpassfilter bei 15 Hz, um den 10-Hz-Ton zu entfernen, und wenden Sie ihn auf das Signal an. (Es wird empfohlen, zur Vermeidung numerischer Fehler bei der Transferfunktion (
ba)-Format das Format der zweiten Ordnung (second-order sections) zu verwenden.)>>> sos = signal.cheby1(10, 1, 15, 'hp', fs=1000, output='sos') >>> filtered = signal.sosfilt(sos, sig) >>> ax2.plot(t, filtered) >>> ax2.set_title('After 15 Hz high-pass filter') >>> ax2.axis([0, 1, -2, 2]) >>> ax2.set_xlabel('Time [s]') >>> plt.tight_layout() >>> plt.show()