scipy.signal.

chirp#

scipy.signal.chirp(t, f0, t1, f1, method='linear', phi=0, vertex_zero=True, *, complex=False)[Quelle]#

Frequenzdurchlaufender Kosinusgenerator.

Im Folgenden sollte 'Hz' als 'Zyklen pro Einheit' interpretiert werden; es gibt hier keine Anforderung, dass die Einheit eine Sekunde ist. Die wichtige Unterscheidung ist, dass die Einheiten der Rotation Zyklen und nicht Radiant sind. Ebenso könnte t eine Messung von Raum statt Zeit sein.

Parameter:
tarray_like

Zeitpunkte, zu denen die Wellenform ausgewertet werden soll.

f0float

Frequenz (z.B. Hz) zur Zeit t=0.

t1float

Zeitpunkt, zu dem f1 angegeben wird.

f1float

Frequenz (z.B. Hz) der Wellenform zur Zeit t1.

method{‘linear’, ‘quadratic’, ‘logarithmic’, ‘hyperbolic’}, optional

Art des Frequenzdurchlaufs. Wenn nicht angegeben, wird linear angenommen. Weitere Details siehe Hinweise unten.

phifloat, optional

Phasenverschiebung in Grad. Standardwert ist 0.

vertex_zerobool, optional

Dieser Parameter wird nur verwendet, wenn method 'quadratic' ist. Er bestimmt, ob der Scheitelpunkt der Parabel, die den Graphen der Frequenz darstellt, bei t=0 oder t=t1 liegt.

complexbool, optional

Dieser Parameter erzeugt ein komplexwertiges analytisches Signal anstelle eines reellwertigen Signals. Er ermöglicht die Verwendung von komplexer Basisband (im Kommunikationsbereich). Standardwert ist False.

Hinzugefügt in Version 1.15.0.

Rückgabe:
yndarray

Ein Numpy-Array, das das zur Zeit t ausgewertete Signal mit der angeforderten zeitvariablen Frequenz enthält. Genauer gesagt gibt die Funktion exp(1j*phase + 1j*(pi/180)*phi) if complex else cos(phase + (pi/180)*phi) zurück, wobei phase das Integral (von 0 bis t) von 2*pi*f(t) ist. Die momentane Frequenz f(t) ist unten definiert.

Siehe auch

sweep_poly

Hinweise

Für den Parameter method gibt es vier mögliche Optionen, die eine (lange) Standardform und einige zulässige Abkürzungen haben. Die Formeln für die momentane Frequenz \(f(t)\) des erzeugten Signals lauten wie folgt:

  1. Parameter method in ('linear', 'lin', 'li')

    \[f(t) = f_0 + \beta\, t \quad\text{mit}\quad \beta = \frac{f_1 - f_0}{t_1}\]

    Die Frequenz \(f(t)\) ändert sich linear über die Zeit mit einer konstanten Rate \(\beta\).

  2. Parameter method in ('quadratic', 'quad', 'q')

    \[\begin{split}f(t) = \begin{cases} f_0 + \beta\, t^2 & \text{wenn vertex_zero True ist,}\\ f_1 + \beta\, (t_1 - t)^2 & \text{andernfalls,} \end{cases} \quad\text{mit}\quad \beta = \frac{f_1 - f_0}{t_1^2}\end{split}\]

    Der Graph der Frequenz f(t) ist eine Parabel durch \((0, f_0)\) und \((t_1, f_1)\). Standardmäßig liegt der Scheitelpunkt der Parabel bei \((0, f_0)\). Wenn vertex_zero False ist, liegt der Scheitelpunkt bei \((t_1, f_1)\). Für eine allgemeinere quadratische Funktion oder ein beliebiges Polynom verwenden Sie die Funktion scipy.signal.sweep_poly.

  3. Parameter method in ('logarithmic', 'log', 'lo')

    \[f(t) = f_0 \left(\frac{f_1}{f_0}\right)^{t/t_1}\]

    \(f_0\) und \(f_1\) müssen ungleich Null sein und das gleiche Vorzeichen haben. Dieses Signal ist auch als geometrischer oder exponentieller Chirp bekannt.

  4. Parameter method in ('hyperbolic', 'hyp')

    \[f(t) = \frac{\alpha}{\beta\, t + \gamma} \quad\text{mit}\quad \alpha = f_0 f_1 t_1, \ \beta = f_0 - f_1, \ \gamma = f_1 t_1\]

    \(f_0\) und \(f_1\) müssen ungleich Null sein.

Beispiele

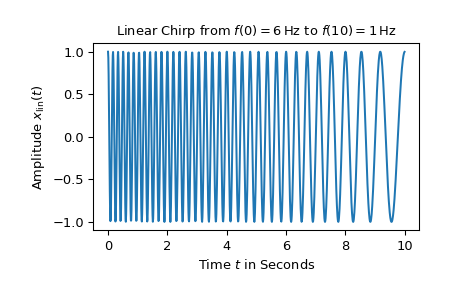
Für das erste Beispiel wird ein linearer Chirp von 6 Hz auf 1 Hz über 10 Sekunden geplottet.

>>> import numpy as np
>>> from matplotlib.pyplot import tight_layout
>>> from scipy.signal import chirp, square, ShortTimeFFT
>>> from scipy.signal.windows import gaussian
>>> import matplotlib.pyplot as plt
...
>>> N, T = 1000, 0.01  # number of samples and sampling interval for 10 s signal
>>> t = np.arange(N) * T  # timestamps
...
>>> x_lin = chirp(t, f0=6, f1=1, t1=10, method='linear')
...
>>> fg0, ax0 = plt.subplots()
>>> ax0.set_title(r"Linear Chirp from $f(0)=6\,$Hz to $f(10)=1\,$Hz")
>>> ax0.set(xlabel="Time $t$ in Seconds", ylabel=r"Amplitude $x_\text{lin}(t)$")
>>> ax0.plot(t, x_lin)
>>> plt.show()
../../_images/scipy-signal-chirp-1_00_00.png

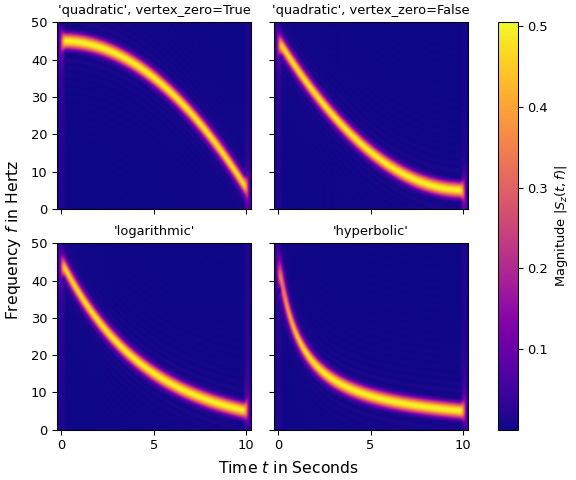
Die folgenden vier Plots zeigen jeweils die kurzzeitige Fourier-Transformation eines Chirps von 45 Hz auf 5 Hz mit unterschiedlichen Werten für den Parameter method (und vertex_zero).

>>> x_qu0 = chirp(t, f0=45, f1=5, t1=N*T, method='quadratic', vertex_zero=True)
>>> x_qu1 = chirp(t, f0=45, f1=5, t1=N*T, method='quadratic', vertex_zero=False)
>>> x_log = chirp(t, f0=45, f1=5, t1=N*T, method='logarithmic')
>>> x_hyp = chirp(t, f0=45, f1=5, t1=N*T, method='hyperbolic')
...
>>> win = gaussian(50, std=12, sym=True)
>>> SFT = ShortTimeFFT(win, hop=2, fs=1/T, mfft=800, scale_to='magnitude')
>>> ts = ("'quadratic', vertex_zero=True", "'quadratic', vertex_zero=False",
...       "'logarithmic'", "'hyperbolic'")
>>> fg1, ax1s = plt.subplots(2, 2, sharex='all', sharey='all',
...                          figsize=(6, 5),  layout="constrained")
>>> for x_, ax_, t_ in zip([x_qu0, x_qu1, x_log, x_hyp], ax1s.ravel(), ts):
...     aSx = abs(SFT.stft(x_))
...     im_ = ax_.imshow(aSx, origin='lower', aspect='auto', extent=SFT.extent(N),
...                      cmap='plasma')
...     ax_.set_title(t_)
...     if t_ == "'hyperbolic'":
...         fg1.colorbar(im_, ax=ax1s, label='Magnitude $|S_z(t,f)|$')
>>> _ = fg1.supxlabel("Time $t$ in Seconds")  # `_ =` is needed to pass doctests
>>> _ = fg1.supylabel("Frequency $f$ in Hertz")
>>> plt.show()
../../_images/scipy-signal-chirp-1_01_00.png

Schließlich wird die kurzzeitige Fourier-Transformation eines komplexwertigen linearen Chirps von -30 Hz bis 30 Hz dargestellt.

>>> z_lin = chirp(t, f0=-30, f1=30, t1=N*T, method="linear", complex=True)
>>> SFT.fft_mode = 'centered'  # needed to work with complex signals
>>> aSz = abs(SFT.stft(z_lin))
...
>>> fg2, ax2 = plt.subplots()
>>> ax2.set_title(r"Linear Chirp from $-30\,$Hz to $30\,$Hz")
>>> ax2.set(xlabel="Time $t$ in Seconds", ylabel="Frequency $f$ in Hertz")
>>> im2 = ax2.imshow(aSz, origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='viridis')
>>> fg2.colorbar(im2, label='Magnitude $|S_z(t,f)|$')
>>> plt.show()
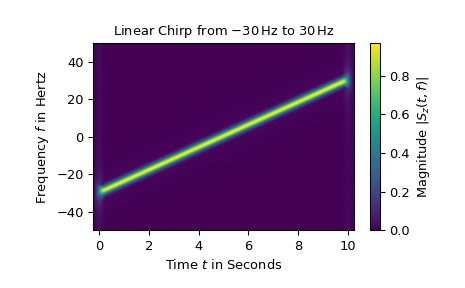
../../_images/scipy-signal-chirp-1_02_00.png

Beachten Sie, dass die Verwendung negativer Frequenzen nur mit komplexwertigen Signalen sinnvoll ist. Darüber hinaus ist die Amplitude der komplexen Exponentialfunktion eins, während die Amplitude der reellwertigen Kosinusfunktion nur 1/2 ist.

Auf dieser Seite