scipy.signal.

cont2discrete#

scipy.signal.cont2discrete(system, dt, method='zoh', alpha=None)[Quellcode]#

Wandelt ein kontinuierliches in ein diskretes Zustandsraum-System um.

Parameter:
systemein Tupel, das das System beschreibt, oder eine Instanz von lti

Das Folgende gibt die Anzahl der Elemente im Tupel und die Interpretation an.

  • 1: (Instanz von lti)

  • 2: (Zähler, Nenner)

  • 3: (Nullstellen, Pole, Verstärkung)

  • 4: (A, B, C, D)

dtfloat

Der Diskretisierungszeitschritt.

methodstr, optional

Welche Methode verwendet werden soll

  • gbt: verallgemeinerte bilineare Transformation

  • bilinear: Tustins Annäherung ("gbt" mit alpha=0.5)

  • euler: Euler-Verfahren (oder Vorwärtsdifferenzierung) ("gbt" mit alpha=0)

  • backward_diff: Rückwärtsdifferenzierung ("gbt" mit alpha=1.0)

  • zoh: Nullstellenhaltefunktion (Standard)

  • foh: Erstorder-Hold (*versionadded: 1.3.0*)

  • impulse: äquivalente Impulsantwort (*versionadded: 1.3.0*)

alphafloat innerhalb von [0, 1], optional

Der Gewichtungsparameter der verallgemeinerten bilinearen Transformation, der nur mit methode="gbt" angegeben werden sollte und ansonsten ignoriert wird.

Rückgabe:
sysdTupel, das das diskrete System enthält

Basierend auf dem Eingabetyp ist die Ausgabe von der Form

  • (Zähler, Nenner, dt) für Übertragungsfunktions-Eingabe

  • (Nullstellen, Pole, Verstärkung, dt) für Nullstellen-Pol-Verstärkungs-Eingabe

  • (A, B, C, D, dt) für Zustandsraum-System-Eingabe

Hinweise

Standardmäßig verwendet die Routine die Zero-Order Hold (zoh)-Methode zur Durchführung der Transformation. Alternativ kann eine verallgemeinerte bilineare Transformation verwendet werden, die die gängige Tustin-Bilinear-Approximation, eine Euler-Methodentechnik oder eine Rückwärtsdifferenzierungstechnik umfasst.

Die Zero-Order Hold (zoh)-Methode basiert auf [1], die verallgemeinerte bilineare Approximation basiert auf [2] und [3], die First-Order Hold (foh)-Methode basiert auf [4].

Referenzen

[3]

G. Zhang, X. Chen und T. Chen, Digital redesign via the generalized bilinear transformation, Int. J. Control, vol. 82, no. 4, pp. 741-754, 2009. (https://www.mypolyuweb.hk/~magzhang/Research/ZCC09_IJC.pdf)

[4]

G. F. Franklin, J. D. Powell und M. L. Workman, Digital control of dynamic systems, 3. Aufl. Menlo Park, Kalifornien: Addison-Wesley, S. 204-206, 1998.

Beispiele

Wir können ein kontinuierliches Zustandsraum-System in ein diskretes umwandeln

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import cont2discrete, lti, dlti, dstep

Definieren Sie ein kontinuierliches Zustandsraum-System.

>>> A = np.array([[0, 1],[-10., -3]])
>>> B = np.array([[0],[10.]])
>>> C = np.array([[1., 0]])
>>> D = np.array([[0.]])
>>> l_system = lti(A, B, C, D)
>>> t, x = l_system.step(T=np.linspace(0, 5, 100))
>>> fig, ax = plt.subplots()
>>> ax.plot(t, x, label='Continuous', linewidth=3)

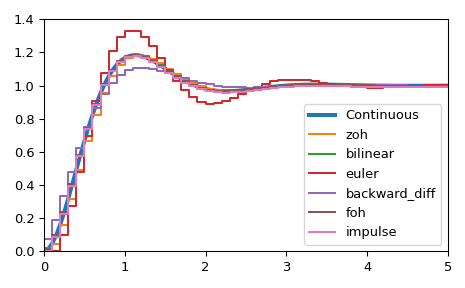
Wandeln Sie es mit verschiedenen Methoden in ein diskretes Zustandsraum-System um.

>>> dt = 0.1
>>> for method in ['zoh', 'bilinear', 'euler', 'backward_diff', 'foh', 'impulse']:
...    d_system = cont2discrete((A, B, C, D), dt, method=method)
...    s, x_d = dstep(d_system)
...    ax.step(s, np.squeeze(x_d), label=method, where='post')
>>> ax.axis([t[0], t[-1], x[0], 1.4])
>>> ax.legend(loc='best')
>>> fig.tight_layout()
>>> plt.show()
../../_images/scipy-signal-cont2discrete-1.png
Auf dieser Seite