correlate#
- scipy.signal.correlate(in1, in2, mode='full', method='auto')[Quelle]#
Kreuzkorrelation zweier N-dimensionaler Arrays.
Kreuzkorreliert in1 und in2, wobei die Größe der Ausgabe durch das Argument mode bestimmt wird.
- Parameter:
- in1array_like
Erster Input.
- in2array_like
Zweiter Input. Sollte dieselbe Anzahl von Dimensionen wie in1 haben.
- modestr {‘full’, ‘valid’, ‘same’}, optional
Ein String, der die Größe der Ausgabe angibt
fullDie Ausgabe ist die vollständige diskrete lineare Kreuzkorrelation der Inputs. (Standard)
validDie Ausgabe besteht nur aus den Elementen, die nicht von der Null-Pufferung abhängen. Im Modus 'valid' muss entweder in1 oder in2 in jeder Dimension mindestens so groß sein wie der andere.
sameDie Ausgabe hat die gleiche Größe wie in1 und ist zentriert bezüglich der 'full'-Ausgabe.
- methodstr {‘auto’, ‘direct’, ‘fft’}, optional
Ein String, der angibt, welche Methode zur Berechnung der Korrelation verwendet werden soll.
directDie Korrelation wird direkt aus Summen bestimmt, der Definition der Korrelation.
fftDie Fast Fourier Transform wird verwendet, um die Korrelation schneller durchzuführen (nur für numerische Arrays verfügbar).
autoWählt automatisch die direkte oder die Fourier-Methode basierend auf einer Schätzung aus, welche schneller ist (Standard). Weitere Details finden Sie in den Anmerkungen zu
convolve.Hinzugefügt in Version 0.19.0.
- Rückgabe:
- correlatearray
Ein N-dimensionales Array, das eine Teilmenge der diskreten linearen Kreuzkorrelation von in1 mit in2 enthält.
Siehe auch
choose_conv_methodenthält weitere Dokumentation zu method.
correlation_lagsberechnet das Lag/Verschiebungsindex-Array für 1D-Kreuzkorrelation.
Hinweise
Die Korrelation z zweier d-dimensionaler Arrays x und y ist definiert als
z[...,k,...] = sum[..., i_l, ...] x[..., i_l,...] * conj(y[..., i_l - k,...])
Auf diese Weise, wenn
xundy1D-Arrays sind undz = correlate(x, y, 'full')dann gilt\[z[k] = \sum_{l=0}^{N-1} x_l \, y_{l-k}^{*}\]für \(k = -(M-1), \dots, (N-1)\), wobei \(N\) die Länge von
xist, \(M\) die Länge vonyist und \(y_m = 0\) ist, wenn \(m\) außerhalb des gültigen Bereichs \([0, M-1]\) liegt. Die Größe von \(z\) ist \(N + M - 1\) und \(y^*\) bezeichnet die komplex Konjugierte von \(y\).method='fft'funktioniert nur für numerische Arrays, da es auffftconvolvebasiert. In bestimmten Fällen (z. B. Arrays von Objekten oder wenn die Rundung von ganzen Zahlen zu Präzisionsverlust führen kann) wird immermethod='direct'verwendet.Wenn
mode='same'mit geradzahligen Input-Längen verwendet wird, unterscheiden sich die Ausgaben voncorrelateundcorrelate2d: Es gibt einen 1-Index-Offset zwischen ihnen.Beispiele
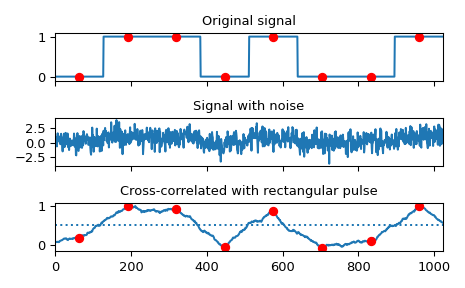
Implementierung eines Matched-Filters mittels Kreuzkorrelation, um ein Signal wiederherzustellen, das durch einen verrauschten Kanal gegangen ist.
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng()
>>> sig = np.repeat([0., 1., 1., 0., 1., 0., 0., 1.], 128) >>> sig_noise = sig + rng.standard_normal(len(sig)) >>> corr = signal.correlate(sig_noise, np.ones(128), mode='same') / 128
>>> clock = np.arange(64, len(sig), 128) >>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, sharex=True) >>> ax_orig.plot(sig) >>> ax_orig.plot(clock, sig[clock], 'ro') >>> ax_orig.set_title('Original signal') >>> ax_noise.plot(sig_noise) >>> ax_noise.set_title('Signal with noise') >>> ax_corr.plot(corr) >>> ax_corr.plot(clock, corr[clock], 'ro') >>> ax_corr.axhline(0.5, ls=':') >>> ax_corr.set_title('Cross-correlated with rectangular pulse') >>> ax_orig.margins(0, 0.1) >>> fig.tight_layout() >>> plt.show()
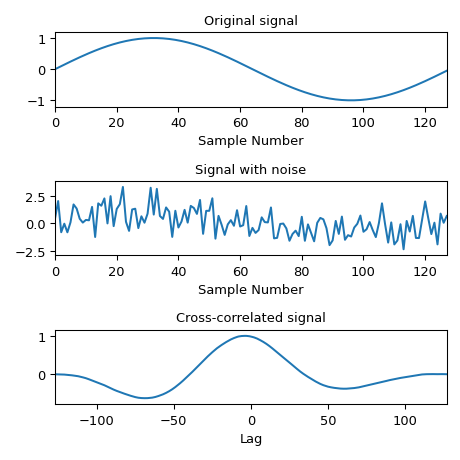
Berechnung der Kreuzkorrelation eines verrauschten Signals mit dem Originalsignal.
>>> x = np.arange(128) / 128 >>> sig = np.sin(2 * np.pi * x) >>> sig_noise = sig + rng.standard_normal(len(sig)) >>> corr = signal.correlate(sig_noise, sig) >>> lags = signal.correlation_lags(len(sig), len(sig_noise)) >>> corr /= np.max(corr)
>>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, figsize=(4.8, 4.8)) >>> ax_orig.plot(sig) >>> ax_orig.set_title('Original signal') >>> ax_orig.set_xlabel('Sample Number') >>> ax_noise.plot(sig_noise) >>> ax_noise.set_title('Signal with noise') >>> ax_noise.set_xlabel('Sample Number') >>> ax_corr.plot(lags, corr) >>> ax_corr.set_title('Cross-correlated signal') >>> ax_corr.set_xlabel('Lag') >>> ax_orig.margins(0, 0.1) >>> ax_noise.margins(0, 0.1) >>> ax_corr.margins(0, 0.1) >>> fig.tight_layout() >>> plt.show()