dfreqresp#
- scipy.signal.dfreqresp(system, w=None, n=10000, whole=False)[Quellcode]#
Berechnet die Frequenzantwort eines zeitdiskreten Systems.
- Parameter:
- systemdlti | tuple
Eine Instanz der LTI-Klasse
dltioder ein Tupel, das das System beschreibt. Die Anzahl der Elemente im Tupel bestimmt die Interpretation. D. h.system: Instanz der LTI-Klassedlti. Beachten Sie, dass abgeleitete Instanzen, wie z. B. Instanzen vonTransferFunction,ZerosPolesGainoderStateSpace, ebenfalls zulässig sind.(num, den, dt): Rationale Polynome, wie inTransferFunctionbeschrieben. Die Koeffizienten der Polynome sollten in absteigender Exponentenreihenfolge angegeben werden, z.B. z² + 3z + 5 würde als[1, 3, 5]dargestellt werden.(zeros, poles, gain, dt): Nullstellen-, Pol-, Verstärkungsform, wie inZerosPolesGainbeschrieben.(A, B, C, D, dt): Zustandsraumform, wie inStateSpacebeschrieben.
- warray_like, optional
Array von Frequenzen (in Radiant/Sample). Amplituden- und Phasendaten werden für jeden Wert in diesem Array berechnet. Wenn nicht angegeben, wird ein angemessenes Set berechnet.
- nint, optional
Anzahl der Frequenzpunkte, die berechnet werden sollen, wenn w nicht angegeben ist. Die n Frequenzen sind logarithmisch in einem Intervall verteilt, das so gewählt wird, dass es den Einfluss der Pole und Nullstellen des Systems erfasst.
- wholebool, optional
Normalerweise, wenn 'w' nicht gegeben ist, werden die Frequenzen von 0 bis zur Nyquist-Frequenz, pi Radiant/Sample (oberer Halbkreis des Einheitskreises), berechnet. Wenn whole True ist, werden die Frequenzen von 0 bis 2*pi Radiant/Sample berechnet.
- Rückgabe:
- w1D ndarray
Frequenz-Array [Radiant/Sample]
- H1D ndarray
Array von komplexen Amplitudenwerten
Hinweise
Wenn (num, den) für
systemübergeben wird, sollten die Koeffizienten für Zähler und Nenner in absteigender Reihenfolge der Exponenten angegeben werden (z. B.z^2 + 3z + 5würde als[1, 3, 5]dargestellt werden).Hinzugefügt in Version 0.18.0.
Beispiele
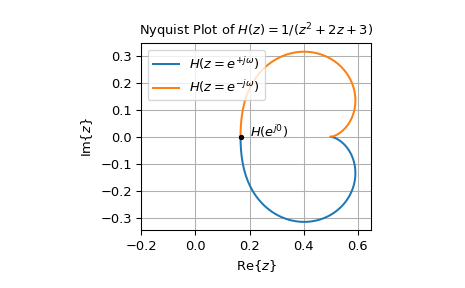
Das folgende Beispiel generiert das Nyquist-Diagramm der Übertragungsfunktion \(H(z) = \frac{1}{z^2 + 2z + 3}\) mit einer Abtastzeit von 0,05 Sekunden
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> sys = signal.TransferFunction([1], [1, 2, 3], dt=0.05) # construct H(z) >>> w, H = signal.dfreqresp(sys) ... >>> fig0, ax0 = plt.subplots() >>> ax0.plot(H.real, H.imag, label=r"$H(z=e^{+j\omega})$") >>> ax0.plot(H.real, -H.imag, label=r"$H(z=e^{-j\omega})$") >>> ax0.set_title(r"Nyquist Plot of $H(z) = 1 / (z^2 + 2z + 3)$") >>> ax0.set(xlabel=r"$\text{Re}\{z\}$", ylabel=r"$\text{Im}\{z\}$", ... xlim=(-0.2, 0.65), aspect='equal') >>> ax0.plot(H[0].real, H[0].imag, 'k.') # mark H(exp(1j*w[0])) >>> ax0.text(0.2, 0, r"$H(e^{j0})$") >>> ax0.grid(True) >>> ax0.legend() >>> plt.show()