scipy.signal.

kaiserord

scipy.signal.kaiserord(ripple, width)

Ermittelt die Filterfensterparameter für die Kaiser-Fenster-Methode.

Die von dieser Funktion zurückgegebenen Parameter werden im Allgemeinen verwendet, um einen FIR-Filter (Finite Impulse Response) mit der Fensterungsmethode zu erstellen, entweder mit firwin oder firwin2.

Parameter:

ripplefloat

Obere Grenze für die Abweichung (in dB) der Amplitude des Frequenzgangs des Filters von der des gewünschten Filters (ohne Frequenzen in Übergangsintervallen). Das heißt, wenn w die Frequenz als Bruchteil der Nyquist-Frequenz ist, A(w) der tatsächliche Frequenzgang des Filters und D(w) der gewünschte Frequenzgang ist, lautet die Entwurfsvorgabe:

abs(A(w) - D(w))) < 10**(-ripple/20)

für 0 <= w <= 1 und w nicht in einem Übergangsintervall.

widthfloat

Breite des Übergangsbereichs, normalisiert so, dass 1 pi Radiant/Sample entspricht. Das heißt, die Frequenz wird als Bruchteil der Nyquist-Frequenz ausgedrückt.

Rückgabe:

numtapsint

Die Länge des Kaiser-Fensters.

betafloat

Der Beta-Parameter für das Kaiser-Fenster.

Siehe auch

kaiser_beta, kaiser_atten

Hinweise

Es gibt mehrere Möglichkeiten, das Kaiser-Fenster zu erhalten:

• signal.windows.kaiser(numtaps, beta, sym=True)

• signal.get_window(beta, numtaps)

• signal.get_window(('kaiser', beta), numtaps)

Es werden die von Kaiser entdeckten empirischen Gleichungen verwendet.

Referenzen

Oppenheim, Schafer, „Discrete-Time Signal Processing“, S. 475-476.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Wir verwenden die Kaiser-Fenster-Methode, um einen Tiefpass-FIR-Filter für ein Signal zu entwerfen, das mit 1000 Hz abgetastet wird.

Wir wünschen eine Dämpfung von mindestens 65 dB im Sperrbereich, und im Durchlassbereich soll der Verstärkungsfaktor nicht mehr als 0,5 % variieren.

Wir wünschen eine Grenzfrequenz von 175 Hz, mit einem Übergang zwischen Durchlass- und Sperrbereich von 24 Hz. Das heißt, im Bereich [0, 163] variiert die Verstärkung nicht mehr als 0,5 %, und im Bereich [187, 500] wird das Signal um mindestens 65 dB gedämpft.

>>> import numpy as np
>>> from scipy.signal import kaiserord, firwin, freqz
>>> import matplotlib.pyplot as plt
>>> fs = 1000.0
>>> cutoff = 175
>>> width = 24

Die Kaiser-Methode akzeptiert nur einen einzigen Parameter, um die Ripple im Durchlassbereich und die Dämpfung im Sperrbereich zu steuern, daher verwenden wir den restriktiveren der beiden. In diesem Fall beträgt die Ripple im Durchlassbereich 0,005, also 46,02 dB, daher werden wir 65 dB als Designparameter verwenden.

Verwenden Sie kaiserord, um die Länge des Filters und den Parameter für das Kaiser-Fenster zu bestimmen.

>>> numtaps, beta = kaiserord(65, width/(0.5*fs))
>>> numtaps
167
>>> beta
6.20426

Verwenden Sie firwin, um den FIR-Filter zu erstellen.

>>> taps = firwin(numtaps, cutoff, window=('kaiser', beta),
...               scale=False, fs=fs)

Berechnen Sie den Frequenzgang des Filters. w ist das Array der Frequenzen und h ist das entsprechende komplexe Array der Frequenzgänge.

>>> w, h = freqz(taps, worN=8000)
>>> w *= 0.5*fs/np.pi  # Convert w to Hz.

Berechnen Sie die Abweichung der Amplitude des Filtergangs von der des idealen Tiefpassfilters. Werte im Übergangsbereich werden auf nan gesetzt, damit sie nicht in der Grafik erscheinen.

>>> ideal = w < cutoff  # The "ideal" frequency response.
>>> deviation = np.abs(np.abs(h) - ideal)
>>> deviation[(w > cutoff - 0.5*width) & (w < cutoff + 0.5*width)] = np.nan

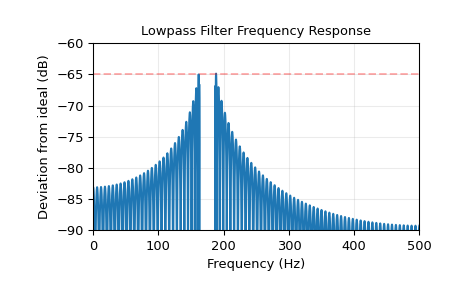
Zeichnen Sie die Abweichung. Ein genauer Blick auf das linke Ende des Sperrbereichs zeigt, dass die Anforderung einer 65 dB-Dämpfung im ersten Lappen um etwa 0,125 dB verletzt wird. Dies ist für die Kaiser-Fenster-Methode nicht ungewöhnlich.

>>> plt.plot(w, 20*np.log10(np.abs(deviation)))
>>> plt.xlim(0, 0.5*fs)
>>> plt.ylim(-90, -60)
>>> plt.grid(alpha=0.25)
>>> plt.axhline(-65, color='r', ls='--', alpha=0.3)
>>> plt.xlabel('Frequency (Hz)')
>>> plt.ylabel('Deviation from ideal (dB)')
>>> plt.title('Lowpass Filter Frequency Response')
>>> plt.show()

ZurückIn Tab öffnen