scipy.signal.

lfilter#

scipy.signal.lfilter(b, a, x, axis=-1, zi=None)[Quelle]#

Daten entlang einer Dimension mit einem IIR- oder FIR-Filter filtern.

Filtert eine Datensequenz, x, mit einem digitalen Filter. Dies funktioniert für viele grundlegende Datentypen (einschließlich Objekttyp). Der Filter ist eine direkte Implementierung der Transponierten Form II der Standard-Differenzgleichung (siehe Anmerkungen).

Die Funktion sosfilt (und Filterdesign mit output='sos') sollte für die meisten Filteraufgaben lfilter vorgezogen werden, da Zweipunktsektionen weniger numerische Probleme aufweisen.

Parameter:

barray_like: Der Zählerkoeffizientenvektor in einer 1D-Sequenz.
aarray_like: Der Nennerkoeffizientenvektor in einer 1D-Sequenz. Wenn a[0] nicht 1 ist, werden sowohl a als auch b durch a[0] normalisiert.
xarray_like: Ein N-dimensionales Eingabearray.
axisint, optional: Die Achse des Eingabedatenarrays, entlang der der lineare Filter angewendet werden soll. Der Filter wird auf jeden Unterarray entlang dieser Achse angewendet. Standard ist -1.
ziarray_like, optional: Anfangsbedingungen für die Filterverzögerungen. Es ist ein Vektor (oder ein Array von Vektoren für eine N-dimensionale Eingabe) der Länge max(len(a), len(b)) - 1. Wenn zi None ist oder nicht angegeben wird, wird eine anfängliche Ruhe angenommen. Siehe lfiltic für weitere Informationen.

Rückgabe:

yarray: Die Ausgabe des digitalen Filters.
zfarray, optional: Wenn zi None ist, wird dies nicht zurückgegeben, andernfalls enthält zf die endgültigen Filterverzögerungswerte.

Siehe auch

lfiltic: Konstruiert Anfangsbedingungen für lfilter.
lfilter_zi: Berechnet den Anfangszustand (stationärer Zustand des Sprungantwort) für lfilter.
filtfilt: Ein Vorwärts-Rückwärts-Filter, um einen Filter mit Nullphasen zu erhalten.
savgol_filter: Ein Savitzky-Golay-Filter.
sosfilt: Filtert Daten unter Verwendung kaskadierter Zweipunktsektionen.
sosfiltfilt: Ein Vorwärts-Rückwärts-Filter, der Zweipunktsektionen verwendet.

Hinweise

Die Filterfunktion wird als direkte II-transponierte Struktur implementiert. Das bedeutet, dass der Filter Folgendes implementiert:

a[0]*y[n] = b[0]*x[n] + b[1]*x[n-1] + ... + b[M]*x[n-M]
                      - a[1]*y[n-1] - ... - a[N]*y[n-N]

wobei M der Grad des Zählers ist, N der Grad des Nenners ist und n die Stichprobennummer ist. Es wird mit den folgenden Differenzgleichungen implementiert (unter der Annahme M = N):

a[0]*y[n] = b[0] * x[n]               + d[0][n-1]
  d[0][n] = b[1] * x[n] - a[1] * y[n] + d[1][n-1]
  d[1][n] = b[2] * x[n] - a[2] * y[n] + d[2][n-1]
...
d[N-2][n] = b[N-1]*x[n] - a[N-1]*y[n] + d[N-1][n-1]
d[N-1][n] = b[N] * x[n] - a[N] * y[n]

wobei d die Zustandsvariablen sind.

Die rationale Übertragungsfunktion, die diesen Filter im z-Transformationsbereich beschreibt, lautet:

                    -1              -M
        b[0] + b[1]z  + ... + b[M] z
Y(z) = -------------------------------- X(z)
                    -1              -N
        a[0] + a[1]z  + ... + a[N] z

Beispiele

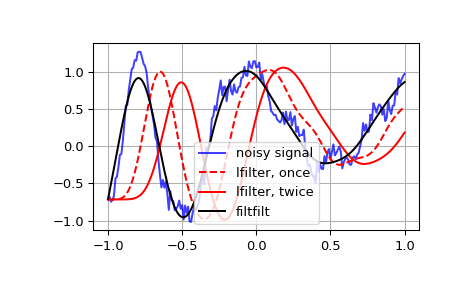
Generieren eines verrauschten Signals zum Filtern

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> t = np.linspace(-1, 1, 201)
>>> x = (np.sin(2*np.pi*0.75*t*(1-t) + 2.1) +
...      0.1*np.sin(2*np.pi*1.25*t + 1) +
...      0.18*np.cos(2*np.pi*3.85*t))
>>> xn = x + rng.standard_normal(len(t)) * 0.08

Erstellen eines Tiefpass-Butterworth-Filters 3. Ordnung

>>> b, a = signal.butter(3, 0.05)

Anwenden des Filters auf xn. Verwenden Sie lfilter_zi, um die Anfangsbedingung des Filters zu wählen

>>> zi = signal.lfilter_zi(b, a)
>>> z, _ = signal.lfilter(b, a, xn, zi=zi*xn[0])

Anwenden des Filters erneut, um ein Ergebnis zu erhalten, das mit einer Ordnung gefiltert wurde, die mit filtfilt übereinstimmt

>>> z2, _ = signal.lfilter(b, a, z, zi=zi*z[0])

Verwenden Sie filtfilt, um den Filter anzuwenden

>>> y = signal.filtfilt(b, a, xn)

Plotten Sie das ursprüngliche Signal und die verschiedenen gefilterten Versionen

>>> plt.figure
>>> plt.plot(t, xn, 'b', alpha=0.75)
>>> plt.plot(t, z, 'r--', t, z2, 'r', t, y, 'k')
>>> plt.legend(('noisy signal', 'lfilter, once', 'lfilter, twice',
...             'filtfilt'), loc='best')
>>> plt.grid(True)
>>> plt.show()

../../_images/scipy-signal-lfilter-1.png