lsim#
- scipy.signal.lsim(system, U, T, X0=None, interp=True)[Quelle]#
Simuliert die Ausgabe eines kontinuierlichen linearen Systems.
- Parameter:
- systemeine Instanz der LTI-Klasse oder ein Tupel, das das System beschreibt.
Das Folgende gibt die Anzahl der Elemente im Tupel und die Interpretation an.
1: (Instanz von
lti)2: (Zähler, Nenner)
3: (Nullstellen, Pole, Verstärkung)
4: (A, B, C, D)
- Uarray_like
Ein Eingangsarray, das die Eingabe zu jeder Zeit T beschreibt (Interpolation wird zwischen gegebenen Zeiten angenommen). Wenn es mehrere Eingänge gibt, dann repräsentiert jede Spalte des Rang-2-Arrays einen Eingang. Wenn U = 0 oder None, wird eine Nulleingabe verwendet.
- Tarray_like
Die Zeitschritte, zu denen die Eingabe definiert ist und zu denen die Ausgabe gewünscht wird. Muss nicht-negativ, aufsteigend und gleichmäßig beabstandet sein.
- X0array_like, optional
Die Anfangsbedingungen für den Zustandsvektor (standardmäßig Null).
- interpbool, optional
Ob für das Eingangsarray eine lineare (True, Standard) oder eine Zero-Order-Hold (False) Interpolation verwendet werden soll.
- Rückgabe:
- T1D ndarray
Zeitwerte für die Ausgabe.
- yout1D ndarray
Systemantwort.
- xoutndarray
Zeitentwicklung des Zustandsvektors.
Hinweise
Wenn (Zähler, Nenner) für
systemübergeben wird, sollten die Koeffizienten für Zähler und Nenner in absteigender Exponentenreihenfolge angegeben werden (z. B.s^2 + 3s + 5würde als[1, 3, 5]dargestellt werden).Beispiele
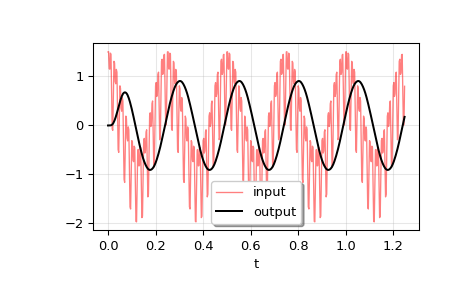
Wir werden
lsimverwenden, um einen analogen Bessel-Filter auf ein Signal anzuwenden.>>> import numpy as np >>> from scipy.signal import bessel, lsim >>> import matplotlib.pyplot as plt
Erstellen Sie einen Tiefpass-Bessel-Filter mit einer Grenzfrequenz von 12 Hz.
>>> b, a = bessel(N=5, Wn=2*np.pi*12, btype='lowpass', analog=True)
Generieren Sie Daten, auf die der Filter angewendet wird.
>>> t = np.linspace(0, 1.25, 500, endpoint=False)
Das Eingangssignal ist die Summe von drei Sinuskurven mit Frequenzen von 4 Hz, 40 Hz und 80 Hz. Der Filter sollte die Komponenten bei 40 Hz und 80 Hz weitgehend eliminieren und nur das 4-Hz-Signal übrig lassen.
>>> u = (np.cos(2*np.pi*4*t) + 0.6*np.sin(2*np.pi*40*t) + ... 0.5*np.cos(2*np.pi*80*t))
Simulieren Sie den Filter mit
lsim.>>> tout, yout, xout = lsim((b, a), U=u, T=t)
Plotten Sie das Ergebnis.
>>> plt.plot(t, u, 'r', alpha=0.5, linewidth=1, label='input') >>> plt.plot(tout, yout, 'k', linewidth=1.5, label='output') >>> plt.legend(loc='best', shadow=True, framealpha=1) >>> plt.grid(alpha=0.3) >>> plt.xlabel('t') >>> plt.show()
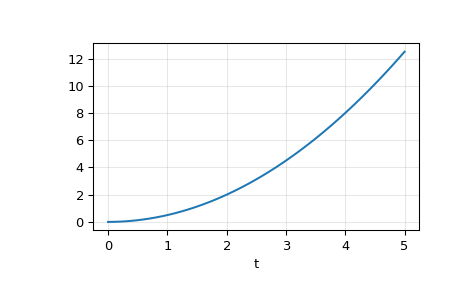
In einem zweiten Beispiel simulieren wir einen doppelten Integrator
y'' = umit einer konstanten Eingabeu = 1. Wir werden die Zustandsraumdarstellung des Integrators verwenden.>>> from scipy.signal import lti >>> A = np.array([[0.0, 1.0], [0.0, 0.0]]) >>> B = np.array([[0.0], [1.0]]) >>> C = np.array([[1.0, 0.0]]) >>> D = 0.0 >>> system = lti(A, B, C, D)
t und u definieren die Zeit und das Eingangssignal für das zu simulierende System.
>>> t = np.linspace(0, 5, num=50) >>> u = np.ones_like(t)
Berechnen Sie die Simulation und plotten Sie dann y. Wie erwartet zeigt der Plot die Kurve
y = 0.5*t**2.>>> tout, y, x = lsim(system, u, t) >>> plt.plot(t, y) >>> plt.grid(alpha=0.3) >>> plt.xlabel('t') >>> plt.show()