scipy.signal.

max_len_seq#

scipy.signal.max_len_seq(nbits, state=None, length=None, taps=None)[Quellcode]#

Maximum-Länge-Sequenz (MLS) Generator.

Parameter:

nbitsint: Anzahl der zu verwendenden Bits. Die Länge der resultierenden Sequenz beträgt (2**nbits) - 1. Beachten Sie, dass die Generierung langer Sequenzen (z. B. größer als nbits == 16) lange dauern kann.
statearray_like, optional: Wenn Array, muss es die Länge nbits haben und wird in seine binäre (boolsche) Darstellung umgewandelt. Wenn None, wird ein Samen aus Einsen verwendet, was eine wiederholbare Darstellung erzeugt. Wenn state nur Nullen enthält, wird ein Fehler ausgelöst, da dies ungültig ist. Standard: None.
lengthint, optional: Anzahl der zu berechnenden Samples. Wenn None, wird die gesamte Länge (2**nbits) - 1 berechnet.
tapsarray_like, optional: Zu verwendende Polynom-Taps (z. B. [7, 6, 1] für eine 8-Bit-Sequenz). Wenn None, werden die Taps automatisch ausgewählt (für bis zu nbits == 32).

Rückgabe:

seqarray: Resultierende MLS-Sequenz aus 0en und 1en.
statearray: Der Endzustand des Schieberegisters.

Hinweise

Der Algorithmus zur Generierung von MLS ist allgemein beschrieben in

https://en.wikipedia.org/wiki/Maximum_length_sequence

Die Standardwerte für Taps werden speziell aus der ersten Option für jeden Wert von nbits ausgewählt, die in

https://web.archive.org/web/20181001062252/http://www.newwaveinstruments.com/resources/articles/m_sequence_linear_feedback_shift_register_lfsr.htm

Hinzugefügt in Version 0.15.0.

Beispiele

MLS verwendet die binäre Konvention

>>> from scipy.signal import max_len_seq
>>> max_len_seq(4)[0]
array([1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0], dtype=int8)

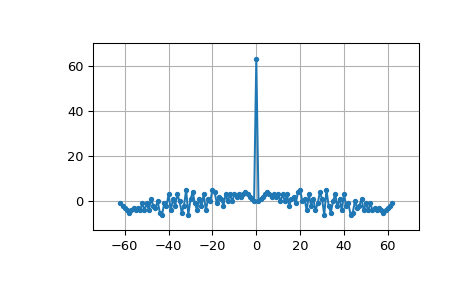
MLS hat ein weißes Spektrum (außer DC)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from numpy.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1  # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
>>> plt.plot(fftshift(fftfreq(N)), fftshift(np.abs(spec)), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

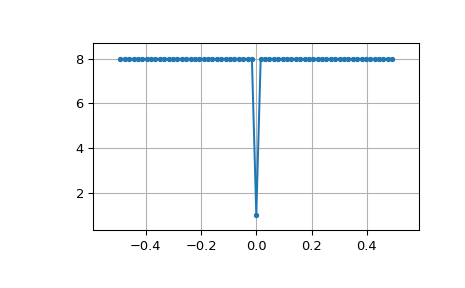
../../_images/scipy-signal-max_len_seq-1_00_00.png

Die zirkuläre Autokorrelation von MLS ist ein Impuls

>>> acorrcirc = ifft(spec * np.conj(spec)).real
>>> plt.figure()
>>> plt.plot(np.arange(-N/2+1, N/2+1), fftshift(acorrcirc), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

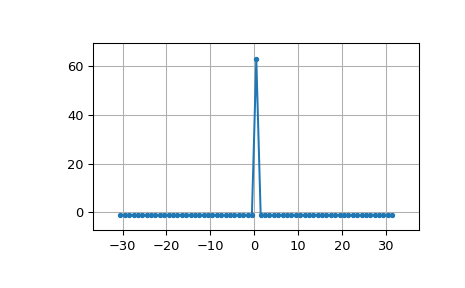
../../_images/scipy-signal-max_len_seq-1_01_00.png

Die lineare Autokorrelation von MLS ist annähernd ein Impuls

>>> acorr = np.correlate(seq, seq, 'full')
>>> plt.figure()
>>> plt.plot(np.arange(-N+1, N), acorr, '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

../../_images/scipy-signal-max_len_seq-1_02_00.png