scipy.signal.

peak_prominences

scipy.signal.peak_prominences(x, peaks, wlen=None)

Berechnet die Prominenz jedes Peaks in einem Signal.

Die Prominenz eines Peaks misst, wie stark ein Peak aus der umgebenden Basislinie des Signals herausragt und ist definiert als der vertikale Abstand zwischen dem Peak und seiner niedrigsten Konturlinie.

Parameter:

xSequenz

Ein Signal mit Peaks.

peaksSequenz

Indizes von Peaks in x.

wlenint, optional

Eine Fensterlänge in Samples, die optional den ausgewerteten Bereich für jeden Peak auf einen Teil von x beschränkt. Der Peak wird immer in der Mitte des Fensters platziert, daher wird die angegebene Länge auf die nächste ungerade Ganzzahl aufgerundet. Dieser Parameter kann die Berechnung beschleunigen (siehe Hinweise).

Rückgabe:

prominencesndarray

Die berechneten Prominenzen für jeden Peak in peaks.

left_bases, right_basesndarray

Die Basen der Peaks als Indizes in x links und rechts von jedem Peak. Die höhere Basis jedes Paares ist die niedrigste Konturlinie eines Peaks.

Löst aus:

ValueError

Wenn ein Wert in peaks ein ungültiger Index für x ist.

Warnungen:

PeakPropertyWarning

Für Indizes in peaks, die nicht auf gültige lokale Maxima in x zeigen, ist die zurückgegebene Prominenz 0 und diese Warnung wird ausgegeben. Dies geschieht auch, wenn wlen kleiner als die Plateaugröße eines Peaks ist.

Warnung

Diese Funktion kann unerwartete Ergebnisse für Daten mit NaNs liefern. Um dies zu vermeiden, sollten NaNs entweder entfernt oder ersetzt werden.

Siehe auch

find_peaks

Findet Spitzen in einem Signal basierend auf Gipfeleigenschaften.

peak_widths

Berechnet die Breite von Peaks.

Hinweise

Strategie zur Berechnung der Prominenz eines Peaks

1. Eine horizontale Linie wird vom aktuellen Peak nach links und rechts verlängert, bis die Linie entweder den Fensterrand erreicht (siehe wlen) oder das Signal an der Steigung eines höheren Peaks wieder schneidet. Ein Schnitt mit einem Peak gleicher Höhe wird ignoriert.

2. Auf jeder Seite wird der minimale Signalwert innerhalb des oben definierten Intervalls gesucht. Diese Punkte sind die Basen des Peaks.

3. Die höhere der beiden Basen markiert die niedrigste Konturlinie des Peaks. Die Prominenz kann dann als vertikaler Unterschied zwischen der Höhe des Peaks selbst und seiner niedrigsten Konturlinie berechnet werden.

Die Suche nach den Basen des Peaks kann für große x mit periodischem Verhalten langsam sein, da für den ersten algorithmischen Schritt große Teile oder sogar das gesamte Signal ausgewertet werden müssen. Dieser Auswertungsbereich kann mit dem Parameter wlen begrenzt werden, der den Algorithmus auf ein Fenster um den aktuellen Peak beschränkt und die Berechnungszeit verkürzen kann, wenn die Fensterlänge kurz im Verhältnis zu x ist. Dies kann jedoch dazu führen, dass der Algorithmus die wahre globale Konturlinie nicht findet, wenn die wahren Basen des Peaks außerhalb dieses Fensters liegen. Stattdessen wird innerhalb des eingeschränkten Fensters eine höhere Konturlinie gefunden, was zu einer geringeren berechneten Prominenz führt. In der Praxis ist dies nur für die höchsten Peaks in x relevant. Dieses Verhalten kann sogar bewusst genutzt werden, um "lokale" Prominenzen zu berechnen.

Hinzugefügt in Version 1.1.0.

Referenzen

[1]

Wikipedia-Artikel über topografische Prominenz: https://en.wikipedia.org/wiki/Topographic_prominence

Beispiele

Probieren Sie es in Ihrem Browser aus!

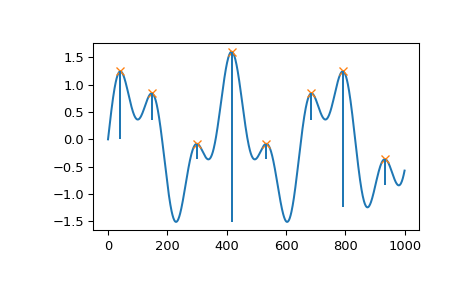
>>> import numpy as np
>>> from scipy.signal import find_peaks, peak_prominences
>>> import matplotlib.pyplot as plt

Erstellen eines Testsignals mit zwei überlagerten Harmonischen

>>> x = np.linspace(0, 6 * np.pi, 1000)
>>> x = np.sin(x) + 0.6 * np.sin(2.6 * x)

Alle Peaks finden und Prominenzen berechnen

>>> peaks, _ = find_peaks(x)
>>> prominences = peak_prominences(x, peaks)[0]
>>> prominences
array([1.24159486, 0.47840168, 0.28470524, 3.10716793, 0.284603  ,
       0.47822491, 2.48340261, 0.47822491])

Höhe der Konturlinie jedes Peaks berechnen und Ergebnisse plotten

>>> contour_heights = x[peaks] - prominences
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.vlines(x=peaks, ymin=contour_heights, ymax=x[peaks])
>>> plt.show()

Wir werten ein zweites Beispiel aus, das mehrere Randfälle für einen Peak bei Index 5 demonstriert.

>>> x = np.array([0, 1, 0, 3, 1, 3, 0, 4, 0])
>>> peaks = np.array([5])
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.show()

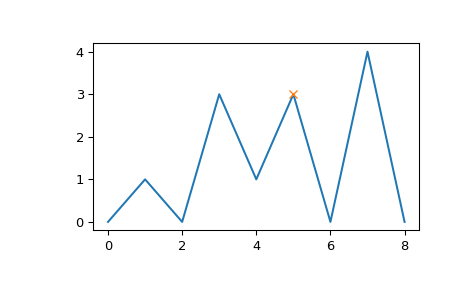
>>> peak_prominences(x, peaks)  # -> (prominences, left_bases, right_bases)
(array([3.]), array([2]), array([6]))

Beachten Sie, wie der Peak bei Index 3 gleicher Höhe bei der Suche nach der linken Basis nicht als Grenze betrachtet wird. Stattdessen werden zwei Minima bei 0 und 2 gefunden, in welchem Fall immer dasjenige näher am ausgewerteten Peak gewählt wird. Auf der rechten Seite muss die Basis jedoch auf 6 gesetzt werden, da der höhere Peak die rechte Grenze des ausgewerteten Bereichs darstellt.

>>> peak_prominences(x, peaks, wlen=3.1)
(array([2.]), array([4]), array([6]))

Hier haben wir den Algorithmus auf ein Fenster von 3 bis 7 beschränkt (die Länge beträgt 5 Samples, da wlen auf die nächste ungerade Ganzzahl aufgerundet wurde). Somit sind die einzigen beiden Kandidaten im ausgewerteten Bereich die beiden benachbarten Samples und eine kleinere Prominenz wird berechnet.

ZurückIn Tab öffnen