scipy.signal.

zoom_fft

scipy.signal.zoom_fft(x, fn, m=None, *, fs=2, endpoint=False, axis=-1)

Berechnet die DFT von x nur für Frequenzen im Bereich fn.

Parameter:

xarray

Das zu transformierende Signal.

fnarray_like

Eine Sequenz der Länge 2 [f1, f2], die den Frequenzbereich angibt, oder ein Skalar, für den der Bereich [0, fn] angenommen wird.

mint, optional

Die Anzahl der auszuwertenden Punkte. Der Standardwert ist die Länge von x.

fsfloat, optional

Die Abtastfrequenz. Wenn fs=10 beispielsweise 10 kHz darstellt, dann würden f1 und f2 ebenfalls in kHz angegeben werden. Die Standard-Abtastfrequenz ist 2, daher sollten f1 und f2 im Bereich [0, 1] liegen, um die Transformation unterhalb der Nyquist-Frequenz zu halten.

endpointbool, optional

Wenn True, ist f2 die letzte Abtastung. Andernfalls ist sie nicht enthalten. Standard ist False.

axisint, optional

Achse, entlang derer die FFT berechnet werden soll. Wenn nicht angegeben, wird die letzte Achse verwendet.

Rückgabe:

outndarray

Das transformierte Signal. Die Fourier-Transformation wird an den Punkten f1, f1+df, f1+2df, ..., f2 berechnet, wobei df=(f2-f1)/m.

Siehe auch

ZoomFFT

Klasse, die eine aufrufbare partielle FFT-Funktion erstellt.

Hinweise

Die Standardwerte sind so gewählt, dass signal.zoom_fft(x, 2) äquivalent zu fft.fft(x) ist und, wenn m > len(x), dass signal.zoom_fft(x, 2, m) äquivalent zu fft.fft(x, m) ist.

Um die Magnitude der resultierenden Transformation zu grafisch darzustellen, verwenden Sie

plot(linspace(f1, f2, m, endpoint=False), abs(zoom_fft(x, [f1, f2], m)))

Wenn die Transformation wiederholt werden muss, verwenden Sie ZoomFFT, um eine spezialisierte Transformationsfunktion zu erstellen, die wiederverwendet werden kann, ohne Konstanten neu zu berechnen.

Beispiele

Probieren Sie es in Ihrem Browser aus!

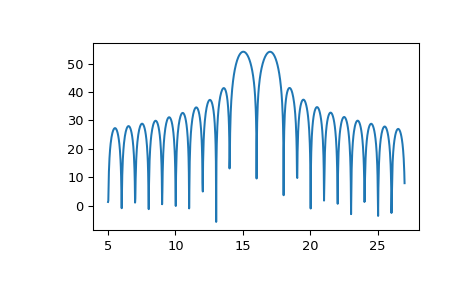
Um die Transformationsergebnisse zu plotten, verwenden Sie etwas Ähnliches wie das Folgende

>>> import numpy as np
>>> from scipy.signal import zoom_fft
>>> t = np.linspace(0, 1, 1021)
>>> x = np.cos(2*np.pi*15*t) + np.sin(2*np.pi*17*t)
>>> f1, f2 = 5, 27
>>> X = zoom_fft(x, [f1, f2], len(x), fs=1021)
>>> f = np.linspace(f1, f2, len(x))
>>> import matplotlib.pyplot as plt
>>> plt.plot(f, 20*np.log10(np.abs(X)))
>>> plt.show()

ZurückIn Tab öffnen