scipy.spatial.

ConvexHull

class scipy.spatial.ConvexHull(points, incremental=False, qhull_options=None)

Konvexe Hüllen in N Dimensionen.

Hinzugefügt in Version 0.12.0.

Parameter:

pointsndarray von floats, Form (npoints, ndim)

Koordinaten der Punkte, aus denen eine konvexe Hülle konstruiert werden soll

incrementalbool, optional

Ermöglicht das schrittweise Hinzufügen neuer Punkte. Dies beansprucht zusätzliche Ressourcen.

qhull_optionsstr, optional

Zusätzliche Optionen, die an Qhull übergeben werden. Siehe Qhull-Handbuch für Details. (Standard: „Qx“ für ndim > 4 und „“ ansonsten) Option „Qt“ ist immer aktiviert.

Attribute:

pointsndarray von double, Form (npoints, ndim)

Koordinaten der Eingabepunkte.

verticesndarray von ints, Form (nvertices,)

Indizes der Punkte, die die Eckpunkte der konvexen Hülle bilden. Bei 2-D-konvexen Hüllen sind die Eckpunkte gegen den Uhrzeigersinn geordnet. In anderen Dimensionen sind sie in der Eingabereihenfolge.

simplicesndarray von ints, Form (nfacet, ndim)

Indizes der Punkte, die die simplizialen Facetten der konvexen Hülle bilden.

neighborsndarray von ints, Form (nfacet, ndim)

Indizes der Nachbarfacetten für jede Facette. Der k-te Nachbar liegt gegenüber dem k-ten Eckpunkt. -1 bedeutet kein Nachbar.

equationsndarray von double, Form (nfacet, ndim+1)

[Normalenvektor, Abstand] der Ebenengleichung der Facette (siehe Qhull-Dokumentation für weitere Informationen).

coplanarndarray von int, Form (ncoplanar, 3)

Indizes von koplanaren Punkten und die entsprechenden Indizes der nächsten Facetten und nächsten Eckpunktindizes. Koplanare Punkte sind Eingabepunkte, die aufgrund von numerischen Präzisionsproblemen *nicht* in die Triangulierung aufgenommen wurden.

Wenn die Option „Qc“ nicht angegeben ist, wird diese Liste nicht berechnet.

goodndarray von bool oder None

Ein eindimensionales boolesches Array, das angibt, welche Facetten „gut“ sind. Wird mit Optionen verwendet, die gute Facetten berechnen, z. B. QGn und QG-n. Gute Facetten sind definiert als diejenigen, die von Punkt n aus sichtbar (n) oder unsichtbar (-n) sind, wobei n der n-te Punkt in ‚points‘ ist. Das Attribut ‚good‘ kann als Index in ‚simplices‘ verwendet werden, um die guten (sichtbaren) Facetten zurückzugeben: simplices[good]. Eine Facette ist nur von außerhalb der Hülle sichtbar, und weder Koplanarität noch Degeneration zählen als Sichtbarkeitsfälle.

Wenn eine „QGn“- oder „QG-n“-Option nicht angegeben ist, wird None zurückgegeben.

Hinzugefügt in Version 1.3.0.

areafloat

Oberflächeninhalt der konvexen Hülle, wenn die Eingabedimension > 2 ist. Wenn die Eingabepoints 2-dimensional ist, ist dies der Umfang der konvexen Hülle.

Hinzugefügt in Version 0.17.0.

volumefloat

Volumen der konvexen Hülle, wenn die Eingabedimension > 2 ist. Wenn die Eingabepoints 2-dimensional ist, ist dies die Fläche der konvexen Hülle.

Hinzugefügt in Version 0.17.0.

Methoden

add_points(points[, restart])	Verarbeitet eine Menge zusätzlicher neuer Punkte.
close()	Beendet die schrittweise Verarbeitung.

Löst aus:

QhullError

Wird ausgelöst, wenn Qhull auf eine Fehlerbedingung stößt, z. B. eine geometrische Degeneration, wenn keine Optionen zur Behebung aktiviert sind.

ValueError

Wird ausgelöst, wenn ein inkompatibles Array als Eingabe gegeben wird.

Hinweise

Die konvexe Hülle wird mit der Qhull-Bibliothek berechnet.

Referenzen

[Qhull]

http://www.qhull.org/

Beispiele

Probieren Sie es in Ihrem Browser aus!

Konvexe Hülle einer zufälligen Punktmenge

>>> from scipy.spatial import ConvexHull, convex_hull_plot_2d
>>> import numpy as np
>>> rng = np.random.default_rng()
>>> points = rng.random((30, 2))   # 30 random points in 2-D
>>> hull = ConvexHull(points)

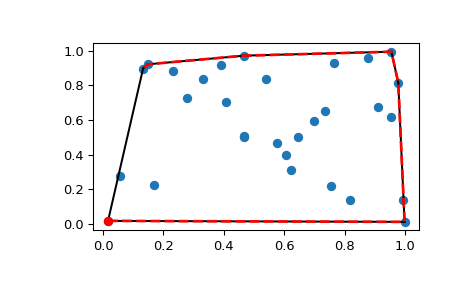
Zeichne sie

>>> import matplotlib.pyplot as plt
>>> plt.plot(points[:,0], points[:,1], 'o')
>>> for simplex in hull.simplices:
...     plt.plot(points[simplex, 0], points[simplex, 1], 'k-')

Wir hätten auch direkt die Eckpunkte der Hülle verwenden können, die bei 2-D garantiert gegen den Uhrzeigersinn geordnet sind

>>> plt.plot(points[hull.vertices,0], points[hull.vertices,1], 'r--', lw=2)
>>> plt.plot(points[hull.vertices[0],0], points[hull.vertices[0],1], 'ro')
>>> plt.show()

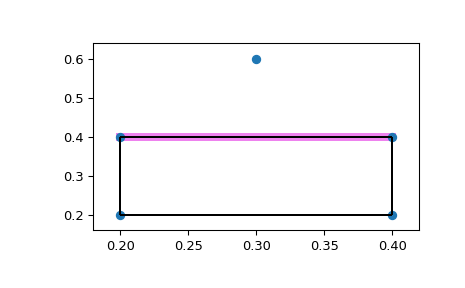
Von einem Punkt aus sichtbare Facetten

Erstellen Sie ein Quadrat und fügen Sie einen Punkt oberhalb des Quadrats hinzu.

>>> generators = np.array([[0.2, 0.2],
...                        [0.2, 0.4],
...                        [0.4, 0.4],
...                        [0.4, 0.2],
...                        [0.3, 0.6]])

Rufen Sie ConvexHull mit der Option QG auf. QG4 bedeutet, die Teile der Hülle zu berechnen, die Punkt 4 nicht einschließen, und gibt die Facetten an, die von Punkt 4 aus sichtbar sind.

>>> hull = ConvexHull(points=generators,
...                   qhull_options='QG4')

Das Array „good“ gibt an, welche Facetten von Punkt 4 aus sichtbar sind.

>>> print(hull.simplices)
    [[1 0]
     [1 2]
     [3 0]
     [3 2]]
>>> print(hull.good)
    [False  True False False]

Nun plotten wir es und heben die sichtbaren Facetten hervor.

>>> fig = plt.figure()
>>> ax = fig.add_subplot(1,1,1)
>>> for visible_facet in hull.simplices[hull.good]:
...     ax.plot(hull.points[visible_facet, 0],
...             hull.points[visible_facet, 1],
...             color='violet',
...             lw=6)
>>> convex_hull_plot_2d(hull, ax=ax)
    <Figure size 640x480 with 1 Axes> # may vary
>>> plt.show()

ZurückIn Tab öffnen