scipy.spatial.

Delaunay#

class scipy.spatial.Delaunay(points, furthest_site=False, incremental=False, qhull_options=None)#

Delaunay-Tessellierung in N Dimensionen.

Hinzugefügt in Version 0.9.

Parameter:

pointsndarray von floats, Form (npoints, ndim): Koordinaten der zu triangulierenden Punkte
furthest_sitebool, optional: Ob eine Delaunay-Triangulierung nach dem am weitesten entfernten Punkt berechnet werden soll. Standard: False

Hinzugefügt in Version 0.12.0.
incrementalbool, optional: Ermöglicht das schrittweise Hinzufügen neuer Punkte. Dies beansprucht zusätzliche Ressourcen.
qhull_optionsstr, optional: Zusätzliche Optionen, die an Qhull übergeben werden. Weitere Details finden Sie im Qhull-Handbuch. Die Option „Qt“ ist immer aktiviert. Standard: „Qbb Qc Qz Qx Q12“ für ndim > 4 und „Qbb Qc Qz Q12“ andernfalls. Der inkrementelle Modus lässt „Qz“ weg.

Hinzugefügt in Version 0.12.0.

Attribute:

pointsndarray von double, Form (npoints, ndim)

Koordinaten der Eingabepunkte.

simplicesndarray von ints, Form (nsimplex, ndim+1)

Indizes der Punkte, die die Simplizes in der Triangulierung bilden. Für 2D sind die Punkte gegen den Uhrzeigersinn orientiert.

neighborsndarray von ints, Form (nsimplex, ndim+1)

Indizes der Nachbarsimplexen für jeden Simplex. Der k-te Nachbar ist gegenüber der k-ten Ecke. Für Simplices am Rand bedeutet -1 keinen Nachbarn.

equationsndarray von double, Form (nsimplex, ndim+2)

[Normalenvektor, Verschiebung], die die Hyperebenengleichung der Facette auf dem Paraboloid bilden (weitere Informationen finden Sie in der Qhull-Dokumentation).

paraboloid_scale, paraboloid_shiftfloat

Skalierung und Verschiebung für die zusätzliche Paraboloiddimension (weitere Informationen finden Sie in der Qhull-Dokumentation).

transformndarray von double, Form (nsimplex, ndim+1, ndim)

Affine Transformation von x zu den baryzentrischen Koordinaten c.

vertex_to_simplexndarray von int, Form (npoints,)

Nachschlagetabelle von einer Ecke zu einem Simplex, zu dem sie gehört.

convex_hullndarray von int, Form (nfaces, ndim)

Ecken der Facetten, die die konvexe Hülle der Punktmenge bilden.

coplanarndarray von int, Form (ncoplanar, 3)

Indizes von koplanaren Punkten und die entsprechenden Indizes der nächstgelegenen Facette und der nächstgelegenen Ecke. Koplanare Punkte sind Eingabepunkte, die aufgrund von numerischen Präzisionsproblemen *nicht* in die Triangulierung aufgenommen wurden.

Wenn die Option „Qc“ nicht angegeben ist, wird diese Liste nicht berechnet.

Hinzugefügt in Version 0.12.0.

vertex_neighbor_verticesTuple aus zwei ndarrays von int; (indptr, indices)

Nachbarecken von Ecken.

furthest_site

True, wenn es sich um eine Triangulierung nach dem am weitesten entfernten Punkt handelte, und False andernfalls.

Hinzugefügt in Version 1.4.0.

Methoden

`add_points`(points[, restart])	Verarbeitet eine Menge zusätzlicher neuer Punkte.
`close`()	Beendet die schrittweise Verarbeitung.
`find_simplex`(self, xi[, bruteforce, tol])	Findet die Simplizes, die die gegebenen Punkte enthalten.
`lift_points`(self, x)	Hebt Punkte auf das Qhull-Paraboloid.
`plane_distance`(self, xi)	Berechnet die Hyperebenenabstände zum Punkt xi von allen Simplizes.

Löst aus:

QhullError: Wird ausgelöst, wenn Qhull auf eine Fehlerbedingung stößt, z. B. eine geometrische Degeneration, wenn keine Optionen zur Behebung aktiviert sind.
ValueError: Wird ausgelöst, wenn ein inkompatibles Array als Eingabe gegeben wird.

Hinweise

Die Tessellierung wird mit der Qhull-Bibliothek berechnet (Qhull-Bibliothek).

Hinweis

Sofern Sie nicht die Qhull-Option „QJ“ übergeben, garantiert Qhull nicht, dass jeder Eingabepunkt als Ecke in der Delaunay-Triangulierung erscheint. Ausgelassene Punkte sind im Attribut coplanar aufgeführt.

Beispiele

Triangulierung einer Punktmenge

>>> import numpy as np
>>> points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])
>>> from scipy.spatial import Delaunay
>>> tri = Delaunay(points)

Wir können sie plotten

>>> import matplotlib.pyplot as plt
>>> plt.triplot(points[:,0], points[:,1], tri.simplices)
>>> plt.plot(points[:,0], points[:,1], 'o')
>>> plt.show()

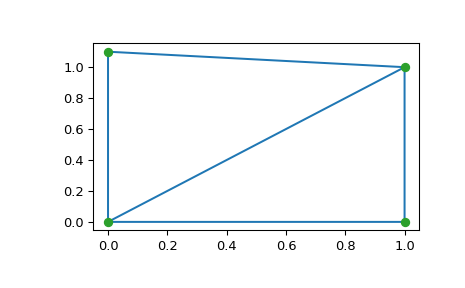
../../_images/scipy-spatial-Delaunay-1_00_00.png

Punktindizes und Koordinaten für die beiden Dreiecke, die die Triangulierung bilden

>>> tri.simplices
array([[2, 3, 0],                 # may vary
       [3, 1, 0]], dtype=int32)

Beachten Sie, dass die Simplizes je nach Rundungsfehlern in einer anderen Reihenfolge als oben sein können.

>>> points[tri.simplices]
array([[[ 1. ,  0. ],            # may vary
        [ 1. ,  1. ],
        [ 0. ,  0. ]],
       [[ 1. ,  1. ],
        [ 0. ,  1.1],
        [ 0. ,  0. ]]])

Dreieck 0 ist der einzige Nachbar von Dreieck 1 und liegt gegenüber der Ecke 1 von Dreieck 1

>>> tri.neighbors[1]
array([-1,  0, -1], dtype=int32)
>>> points[tri.simplices[1,1]]
array([ 0. ,  1.1])

Wir können herausfinden, in welchem Dreieck sich die Punkte befinden

>>> p = np.array([(0.1, 0.2), (1.5, 0.5), (0.5, 1.05)])
>>> tri.find_simplex(p)
array([ 1, -1, 1], dtype=int32)

Die zurückgegebenen ganzen Zahlen im Array sind die Indizes des Simplex, in dem sich der entsprechende Punkt befindet. Wenn -1 zurückgegeben wird, befindet sich der Punkt in keinem Simplex. Beachten Sie, dass die Verknüpfung im folgenden Beispiel nur für gültige Punkte korrekt funktioniert, da ungültige Punkte zu -1 führen, was selbst ein gültiger Index für den letzten Simplex in der Liste ist.

>>> p_valids = np.array([(0.1, 0.2), (0.5, 1.05)])
>>> tri.simplices[tri.find_simplex(p_valids)]
array([[3, 1, 0],                 # may vary
       [3, 1, 0]], dtype=int32)

Wir können auch die baryzentrischen Koordinaten im Dreieck 1 für diese Punkte berechnen

>>> b = tri.transform[1,:2].dot(np.transpose(p - tri.transform[1,2]))
>>> np.c_[np.transpose(b), 1 - b.sum(axis=0)]
array([[ 0.1       ,  0.09090909,  0.80909091],
       [ 1.5       , -0.90909091,  0.40909091],
       [ 0.5       ,  0.5       ,  0.        ]])

Die Koordinaten des ersten Punktes sind alle positiv, was bedeutet, dass er sich tatsächlich innerhalb des Dreiecks befindet. Der dritte Punkt liegt auf einer Kante, daher ist seine dritte Koordinate Null.