scipy.spatial.transform.

RigidTransform

class scipy.spatial.transform.RigidTransform

Starre Transformation in 3 Dimensionen.

Diese Klasse bietet eine Schnittstelle zur Initialisierung und Darstellung starrer Transformationen (Rotation und Translation) im 3D-Raum. In verschiedenen Fachgebieten kann dieser Transformationstyp als „Pose“ (insbesondere in der Robotik), „extrinsic parameters“ oder „Model Matrix“ (insbesondere in der Computergrafik) bezeichnet werden, aber das Kernkonzept ist dasselbe: eine Rotation und Translation, die die Ausrichtung eines 3D-Koordinatensystems relativ zu einem anderen beschreiben. Mathematisch gehören diese Transformationen zur speziellen euklidischen Gruppe SE(3), die Rotation (SO(3)) plus Translation kodiert.

Die folgenden Operationen auf starren Transformationen werden unterstützt

• Anwendung auf Vektoren

• Transformationskomposition

• Transformationsinversion

• Transformationsindizierung

Beachten Sie, dass Koordinatensysteme rechtshändig sein müssen. Aus diesem Grund stellt diese Klasse präziser *eigentliche* starre Transformationen in SE(3) dar als starre Transformationen in E(3) im Allgemeinen [1].

Indizierung innerhalb einer Transformation wird unterstützt, da mehrere Transformationen in einer einzigen RigidTransform-Instanz gespeichert werden können.

Zur Erstellung von RigidTransform-Objekten verwenden Sie die Methoden from_... (siehe Beispiele unten). RigidTransform(...) soll nicht direkt instanziiert werden.

Für strenge Einführungen in starre Transformationen siehe [2], [3] und [4].

Attribute:

single

Ob diese Instanz eine einzelne Transformation darstellt.

Rotation

Gibt die Rotationskomponente der Transformation zurück.

Translation

Gibt die Translation-Komponente der Transformation zurück.

Methoden

__len__(self)	Gibt die Anzahl der Transformationen in diesem Objekt zurück.
__getitem__(self, indexer)	Extrahiert Transformation(en) an den angegebenen Indizes aus diesem Objekt.
__mul__(self, RigidTransform other)	Komponiert diese Transformation mit der anderen.
__pow__(self, float n)	Komponiert diese Transformation mit sich selbst n Mal.
from_matrix(cls, matrix)	Initialisiert aus einer 4x4 Transformationsmatrix.
from_rotation(cls, rotation)	Initialisiert aus einer Rotation, ohne Translation.
from_translation(cls, translation)	Initialisiert aus einem Translation-NumPy-Array, ohne Rotation.
from_components(cls, translation, rotation)	Initialisiert eine starre Transformation aus Translations- und Rotationskomponenten.
from_exp_coords(cls, exp_coords)	Initialisiert aus exponentiellen Koordinaten der Transformation.
from_dual_quat(cls, dual_quat, *[, scalar_first])	Initialisiert aus einem Einheits-Dual-Quaternion.
as_matrix(self)	Gibt eine Kopie der Matrixdarstellung der Transformation zurück.
as_components(self)	Gibt die Translations- und Rotationskomponenten der Transformation zurück, wobei die Rotation zuerst angewendet wird, gefolgt von der Translation.
as_exp_coords(self)	Gibt die exponentiellen Koordinaten der Transformation zurück.
as_dual_quat(self, *[, scalar_first])	Gibt die Dual-Quaternion-Darstellung der Transformation zurück.
concatenate(cls, transforms)	Verkettet eine Sequenz von RigidTransform-Objekten zu einem einzigen Objekt.
apply(self, vector[, inverse])	Wendet die Transformation auf einen Vektor an.
inv(self)	Kehrt diese Transformation um.
identity(cls[, num])	Initialisiert eine Identitätstransformation.

Hinweise

Hinzugefügt in Version 1.16.0.

Referenzen

[1]

https://en.wikipedia.org/wiki/Rigid_transformation

[2]

https://motion.cs.illinois.edu/RoboticSystems/CoordinateTransformations.html

[3]

https://www.brainvoyager.com/bv/doc/UsersGuide/CoordsAndTransforms/SpatialTransformationMatrices.html

[4]

Kevin M. Lynch und Frank C. Park, „Modern Robotics: Mechanics, Planning, and Control“, Kapitel 3.3, 2017, Cambridge University Press. https://hades.mech.northwestern.edu/images/2/25/MR-v2.pdf#page=107.31

[5]

Paul Furgale, „Representing Robot Pose: The good, the bad, and the ugly“, 9. Juni 2014. https://rpg.ifi.uzh.ch/docs/teaching/2024/FurgaleTutorial.pdf

Beispiele

Probieren Sie es in Ihrem Browser aus!

Eine Instanz von RigidTransform kann in jedem der oben genannten Formate initialisiert und in jedes der anderen konvertiert werden. Das zugrunde liegende Objekt ist unabhängig von der für die Initialisierung verwendeten Darstellung.

Notation und Kompositionskonventionen

Die Notation folgt weitgehend der in [5] definierten Konvention. Wenn wir Transformationen benennen, lesen wir die Indizes von rechts nach links. tf_A_B stellt also eine Transformation A <- B dar und kann interpretiert werden als

• die Koordinaten und Ausrichtung von B relativ zu A

• die Transformation von Punkten von B nach A

• die Pose von B, beschrieben im Koordinatensystem von A

tf_A_B
   ^ ^
   | |
   | --- from B
   |
   ----- to A

Bei der Komposition von Transformationen ist die Reihenfolge wichtig. Transformationen sind nicht kommutativ, daher ist im Allgemeinen tf_A_B * tf_B_C nicht dasselbe wie tf_B_C * tf_A_B. Transformationen werden von rechts nach links komponiert und auf Vektoren angewendet. Daher ist (tf_A_B * tf_B_C).apply(p_C) dasselbe wie tf_A_B.apply(tf_B_C.apply(p_C)).

Bei der Komposition sollten Transformationen so geordnet sein, dass der Multiplikationsoperator von einem einzelnen Rahmen umgeben ist, sodass der Rahmen „sich aufhebt“ und die äußeren Rahmen übrig bleiben. Im folgenden Beispiel hebt sich B auf und die äußeren Rahmen A und C bleiben übrig. Oder anders ausgedrückt: A <- C ist dasselbe wie A <- B <- C.

              ----------- B cancels out
              |      |
              v      v
tf_A_C = tf_A_B * tf_B_C
            ^          ^
            |          |
            ------------ to A, from C are left

Wenn wir Vektoren notieren, schreiben wir den Index des Rahmens, in dem der Vektor definiert ist. p_B bedeutet also den Punkt p, der im Rahmen B definiert ist. Um diesen Punkt vom Rahmen B in Koordinaten im Rahmen A zu transformieren, wenden wir die Transformation tf_A_B auf den Vektor an und ordnen die Dinge so an, dass die notierten Rahmen B nebeneinander stehen und sich „aufheben“.

           ------------ B cancels out
           |         |
           v         v
p_A = tf_A_B.apply(p_B)
         ^
         |
         -------------- A is left

Visualisierung

>>> from scipy.spatial.transform import RigidTransform as Tf
>>> from scipy.spatial.transform import Rotation as R
>>> import numpy as np

Die folgende Funktion kann verwendet werden, um Transformationen mit Matplotlib zu plotten, indem gezeigt wird, wie sie die Standard-x-, y-, z-Koordinatenachsen transformieren.

>>> import matplotlib.pyplot as plt
>>> colors = ("#FF6666", "#005533", "#1199EE")  # Colorblind-safe RGB
>>> def plot_transformed_axes(ax, tf, name=None, scale=1):
...     r = tf.rotation
...     t = tf.translation
...     loc = np.array([t, t])
...     for i, (axis, c) in enumerate(zip((ax.xaxis, ax.yaxis, ax.zaxis),
...                                       colors)):
...         axlabel = axis.axis_name
...         axis.set_label_text(axlabel)
...         axis.label.set_color(c)
...         axis.line.set_color(c)
...         axis.set_tick_params(colors=c)
...         line = np.zeros((2, 3))
...         line[1, i] = scale
...         line_rot = r.apply(line)
...         line_plot = line_rot + loc
...         ax.plot(line_plot[:, 0], line_plot[:, 1], line_plot[:, 2], c)
...         text_loc = line[1]*1.2
...         text_loc_rot = r.apply(text_loc)
...         text_plot = text_loc_rot + t
...         ax.text(*text_plot, axlabel.upper(), color=c,
...                 va="center", ha="center")
...     ax.text(*tf.translation, name, color="k", va="center", ha="center",
...             bbox={"fc": "w", "alpha": 0.8, "boxstyle": "circle"})

Rahmen definieren

Arbeiten wir ein Beispiel durch.

Definieren Sie zunächst den „Weltrahmen“ A, auch als „Basisrahmen“ bezeichnet. Alle Rahmen sind aus ihrer eigenen Perspektive die Identitätstransformation.

>>> tf_A = Tf.identity()

Wir werden einen neuen Rahmen B im Koordinatensystem von A visualisieren. Daher müssen wir die Transformation definieren, die Koordinaten von Rahmen B nach Rahmen A konvertiert (A <- B).

Physikalisch stellen wir uns vor, B aus A zu konstruieren durch

1. Rotation von A um +90 Grad um seine x-Achse.

2. Translation des rotierten Rahmens um 2 Einheiten in A's -x-Richtung.

Aus A's Perspektive befindet sich B bei [-2, 0, 0] und ist um +90 Grad um die x-Achse gedreht, was genau der Transformation A <- B entspricht.

>>> t_A_B = np.array([-2, 0, 0])
>>> r_A_B = R.from_euler('xyz', [90, 0, 0], degrees=True)
>>> tf_A_B = Tf.from_components(t_A_B, r_A_B)

Lassen Sie uns diese Rahmen plotten.

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> ax.set_title("A, B frames with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

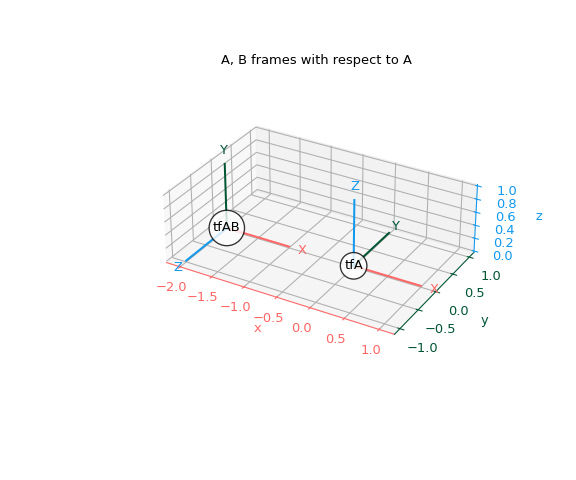
Visualisieren wir nun einen neuen Rahmen C im Koordinatensystem von B. Stellen wir uns vor, C aus B zu konstruieren durch

1. Translation von B um 2 Einheiten in seiner +z-Richtung.

2. Rotation von B um +30 Grad um seine z-Achse.

>>> t_B_C = np.array([0, 0, 2])
>>> r_B_C = R.from_euler('xyz', [0, 0, 30], degrees=True)
>>> tf_B_C = Tf.from_components(t_B_C, r_B_C)

Um diese Rahmen aus einer konsistenten Perspektive zu plotten, müssen wir die Transformation zwischen A und C berechnen. Beachten Sie, dass wir diese Transformation nicht direkt erstellen, sondern zwischenkomponierte Transformationen ableiten, die es uns ermöglichen, von C nach A zu gelangen.

>>> tf_A_C = tf_A_B * tf_B_C  # A <- B <- C

Nun können wir diese drei Rahmen aus A's Perspektive plotten.

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> plot_transformed_axes(ax, tf_A_C, name="tfAC")  # C plotted in A
>>> ax.set_title("A, B, C frames with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

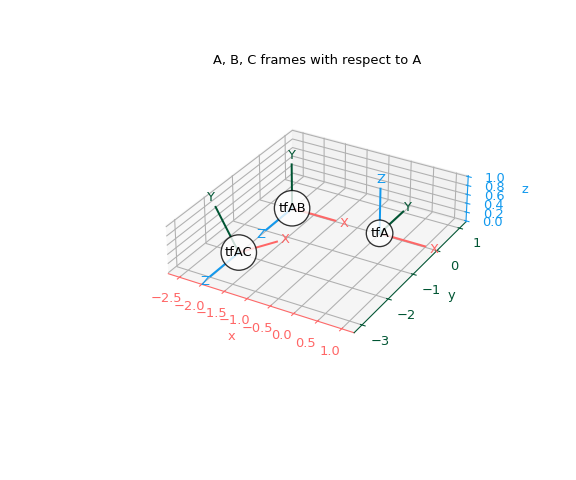
Vektoren transformieren

Lassen Sie uns einen Vektor von A nach B und C transformieren. Dazu invertieren wir zunächst die bereits vorhandenen Transformationen von B und C nach A.

>>> tf_B_A = tf_A_B.inv()  # B <- A
>>> tf_C_A = tf_A_C.inv()  # C <- A

Nun können wir einen Punkt in A definieren und die obigen Transformationen verwenden, um seine Koordinaten in B und C zu erhalten.

>>> p1_A = np.array([1, 0, 0])  # +1 in x_A direction
>>> p1_B = tf_B_A.apply(p1_A)
>>> p1_C = tf_C_A.apply(p1_A)
>>> print(p1_A)  # Original point 1 in A
[1 0 0]
>>> print(p1_B)  # Point 1 in B
[3. 0. 0.]
>>> print(p1_C)  # Point 1 in C
[ 2.59807621 -1.5       -2.        ]

Wir können auch umgekehrt vorgehen. Wir definieren einen Punkt in C und transformieren ihn nach A.

>>> p2_C = np.array([0, 1, 0])  # +1 in y_C direction
>>> p2_A = tf_A_C.apply(p2_C)
>>> print(p2_C)  # Original point 2 in C
[0 1 0]
>>> print(p2_A)  # Point 2 in A
[-2.5       -2.         0.8660254]

Plotten Sie die Rahmen erneut im Verhältnis zu A, aber plotten Sie auch diese beiden Punkte.

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> plot_transformed_axes(ax, tf_A_C, name="tfAC")  # C plotted in A
>>> ax.scatter(p1_A[0], p1_A[1], p1_A[2], color=colors[0])  # +1 x_A
>>> ax.scatter(p2_A[0], p2_A[1], p2_A[2], color=colors[1])  # +1 y_C
>>> ax.set_title("A, B, C frames and points with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

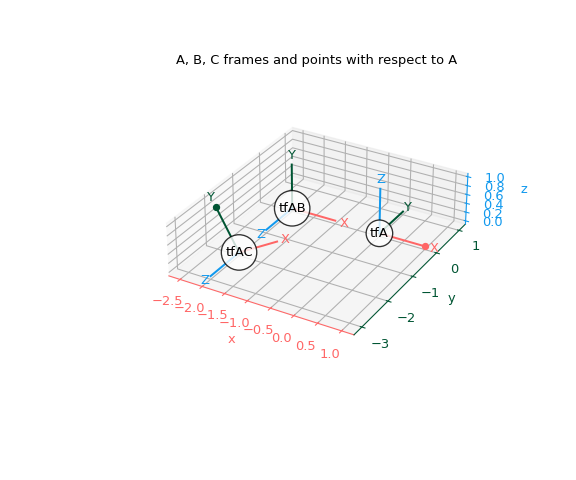
Basisrahmen wechseln

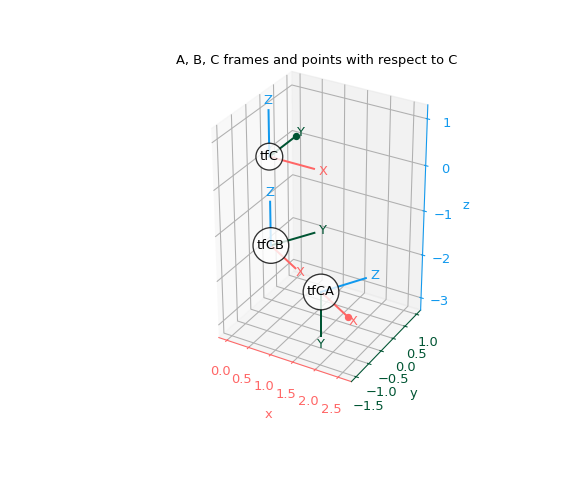
Bis zu diesem Punkt haben wir die Rahmen aus A's Perspektive visualisiert. Verwenden wir die definierten Transformationen, um die Rahmen aus C's Perspektive zu visualisieren.

Nun ist C der „Basisrahmen“ oder „Weltrahmen“. Alle Rahmen sind aus ihrer eigenen Perspektive die Identitätstransformation.

>>> tf_C = Tf.identity()

Wir haben bereits die Transformation C <- A definiert und können C <- B ableiten, indem wir die vorhandene Transformation B <- C invertieren.

>>> tf_C_B = tf_B_C.inv()  # C <- B

Dies ermöglicht es uns, alles aus C's Perspektive zu plotten.

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_C, name="tfC")     # C plotted in C
>>> plot_transformed_axes(ax, tf_C_B, name="tfCB")  # B plotted in C
>>> plot_transformed_axes(ax, tf_C_A, name="tfCA")  # A plotted in C
>>> ax.scatter(p1_C[0], p1_C[1], p1_C[2], color=colors[0])
>>> ax.scatter(p2_C[0], p2_C[1], p2_C[2], color=colors[1])
>>> ax.set_title("A, B, C frames and points with respect to C")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

ZurückIn Tab öffnen