scipy.special.fdtrc#

scipy.special.fdtrc(dfn, dfd, x, out=None) = <ufunc 'fdtrc'>#

F-Überlebensfunktion.

Gibt die komplementäre F-Verteilungsfunktion zurück (das Integral der Dichte von x bis unendlich).

Parameter:

dfnarray_like: Erster Parameter (positive Gleitkommazahl).
dfdarray_like: Zweiter Parameter (positive Gleitkommazahl).
xarray_like: Argument (nicht-negative Gleitkommazahl).
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

yskalar oder ndarray: Die komplementäre F-Verteilungsfunktion mit den Parametern dfn und dfd an der Stelle x.

Siehe auch

fdtr: F-Verteilung kumulative Verteilungsfunktion
fdtri: Inverse Verteilungsfunktion der F-Verteilung
scipy.stats.f: F-Verteilung

Hinweise

Die regularisierte unvollständige Betafunktion wird gemäß der Formel verwendet:

\[F(d_n, d_d; x) = I_{d_d/(d_d + xd_n)}(d_d/2, d_n/2).\]

Wrapper für die Cephes [1] Routine fdtrc. Die F-Verteilung ist auch als scipy.stats.f verfügbar. Das direkte Aufrufen von fdtrc kann die Leistung im Vergleich zur Methode sf von scipy.stats.f verbessern (siehe letztes Beispiel unten).

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Berechnen Sie die Funktion für dfn=1 und dfd=2 bei x=1.

>>> import numpy as np
>>> from scipy.special import fdtrc
>>> fdtrc(1, 2, 1)
0.42264973081037427

Berechnen Sie die Funktion an mehreren Punkten, indem Sie ein NumPy-Array für x angeben.

>>> x = np.array([0.5, 2., 3.])
>>> fdtrc(1, 2, x)
array([0.5527864 , 0.29289322, 0.22540333])

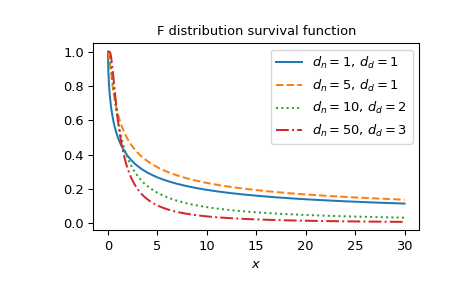
Plotten Sie die Funktion für mehrere Parametersätze.

>>> import matplotlib.pyplot as plt
>>> dfn_parameters = [1, 5, 10, 50]
>>> dfd_parameters = [1, 1, 2, 3]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(dfn_parameters, dfd_parameters,
...                            linestyles))
>>> x = np.linspace(0, 30, 1000)
>>> fig, ax = plt.subplots()
>>> for parameter_set in parameters_list:
...     dfn, dfd, style = parameter_set
...     fdtrc_vals = fdtrc(dfn, dfd, x)
...     ax.plot(x, fdtrc_vals, label=rf"$d_n={dfn},\, d_d={dfd}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$x$")
>>> ax.set_title("F distribution survival function")
>>> plt.show()

../../_images/scipy-special-fdtrc-1_00_00.png

Die F-Verteilung ist auch als scipy.stats.f verfügbar. Die direkte Verwendung von fdtrc kann wesentlich schneller sein als das Aufrufen der Methode sf von scipy.stats.f, insbesondere für kleine Arrays oder einzelne Werte. Um die gleichen Ergebnisse zu erzielen, muss die folgende Parametrisierung verwendet werden: stats.f(dfn, dfd).sf(x)=fdtrc(dfn, dfd, x).

>>> from scipy.stats import f
>>> dfn, dfd = 1, 2
>>> x = 1
>>> fdtrc_res = fdtrc(dfn, dfd, x)  # this will often be faster than below
>>> f_dist_res = f(dfn, dfd).sf(x)
>>> f_dist_res == fdtrc_res  # test that results are equal
True