scipy.special.gamma#

scipy.special.gamma(z, out=None) = <ufunc 'gamma'>#

Gammunktion.

Die Gammunktion ist definiert als

\[\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt\]

für \(\Re(z) > 0\) und wird durch analytische Fortsetzung auf den Rest der komplexen Ebene erweitert. Siehe [dlmf] für weitere Details.

Parameter:

zarray_like: Reeller oder komplexwertiger Argument
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

skalar oder ndarray: Werte der Gammunktion

Hinweise

Die Gammunktion wird oft als verallgemeinerte Fakultät bezeichnet, da \(\Gamma(n + 1) = n!\) für natürliche Zahlen \(n\) gilt. Allgemeiner erfüllt sie die Rekursionsgleichung \(\Gamma(z + 1) = z \cdot \Gamma(z)\) für komplexe \(z\), was in Kombination mit der Tatsache, dass \(\Gamma(1) = 1\) gilt, die obige Identität für \(z = n\) impliziert.

Die Gammunktion hat Pole bei nicht-negativen ganzen Zahlen, und das Vorzeichen der Unendlichkeit beim Annähern jedes Pols hängt von der Richtung ab, aus der sich der Pol nähert. Aus diesem Grund ist es konsistent, dass gamma(z) NaN bei negativen ganzen Zahlen zurückgibt und -inf zurückgibt, wenn x = -0.0 und +inf, wenn x = 0.0, wobei das Vorzeichenbit von Null verwendet wird, um die Richtung anzuzeigen, aus der sich der Ursprung nähert. Dies wird beispielsweise für die Gammunktion in Anhang F, Eintrag 9.5.4 des ISO C 99-Standards empfohlen [isoc99].

Vor SciPy Version 1.15 gab scipy.special.gamma(z) an jedem Pol +inf zurück. Dies wurde in Version 1.15 behoben, allerdings mit der folgenden Konsequenz. Ausdrücke, bei denen Gamma im Nenner vorkommt, wie z. B.:

gamma(u) * gamma(v) / (gamma(w) * gamma(x))

werden nicht mehr zu 0 evaluiert, wenn der Zähler wohldefiniert ist, aber ein Pol im Nenner vorhanden ist. Stattdessen werden solche Ausdrücke zu NaN evaluiert. Wir empfehlen stattdessen die Verwendung der Funktion rgamma für die reziproke Gammunktion in solchen Fällen. Der obige Ausdruck könnte beispielsweise wie folgt geschrieben werden:

gamma(u) * gamma(v) * (rgamma(w) * rgamma(x))

Referenzen

[dlmf]

NIST Digital Library of Mathematical Functions https://dlmf.nist.gov/5.2#E1

[isoc99]

https://www.open-std.org/jtc1/sc22/wg14/www/docs/n1256.pdf

Beispiele

>>> import numpy as np
>>> from scipy.special import gamma, factorial

>>> gamma([0, 0.5, 1, 5])
array([         inf,   1.77245385,   1.        ,  24.        ])

>>> z = 2.5 + 1j
>>> gamma(z)
(0.77476210455108352+0.70763120437959293j)
>>> gamma(z+1), z*gamma(z)  # Recurrence property
((1.2292740569981171+2.5438401155000685j),
 (1.2292740569981158+2.5438401155000658j))

>>> gamma(0.5)**2  # gamma(0.5) = sqrt(pi)
3.1415926535897927

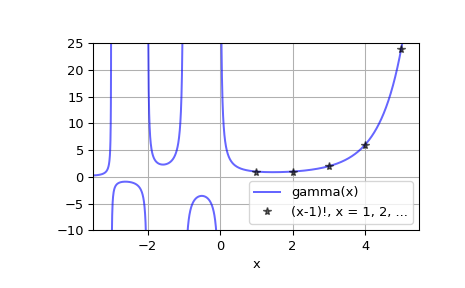
Plot gamma(x) für reelles x

>>> x = np.linspace(-3.5, 5.5, 2251)
>>> y = gamma(x)

>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'b', alpha=0.6, label='gamma(x)')
>>> k = np.arange(1, 7)
>>> plt.plot(k, factorial(k-1), 'k*', alpha=0.6,
...          label='(x-1)!, x = 1, 2, ...')
>>> plt.xlim(-3.5, 5.5)
>>> plt.ylim(-10, 25)
>>> plt.grid()
>>> plt.xlabel('x')
>>> plt.legend(loc='lower right')
>>> plt.show()