scipy.special.mathieu_sem#
- scipy.special.mathieu_sem(m, q, x, out=None) = <ufunc 'mathieu_sem'>#
Ungerade Mathieufunktion und ihre Ableitung
Gibt die ungerade Mathieufunktion se_m(x, q) der Ordnung m und des Parameters q ausgewertet an x (gegeben in Grad) zurück. Gibt auch die Ableitung nach x von se_m(x, q) zurück.
- Parameter:
- marray_like
Ordnung der Funktion
- qarray_like
Parameter der Funktion
- xarray_like
Argument der Funktion, in Grad angegeben, nicht in Radiant.
- outtuple von ndarray, optional
Optionale Ausgabe-Arrays für die Funktionsergebnisse
- Rückgabe:
- yskalar oder ndarray
Wert der Funktion
- ypSkalar oder ndarray
Wert der Ableitung bezüglich x
Siehe auch
Hinweise
Ungerade Mathieufunktionen sind die Lösungen der Mathieu’schen Differentialgleichung
\[\frac{d^2y}{dx^2} + (b_m - 2q \cos(2x))y = 0\]für die die charakteristische Zahl \(b_m\) (berechnet mit
mathieu_b) zu einer ungeraden, periodischen Lösung \(y(x)\) mit Periode 180 Grad (für gerade \(m\)) oder 360 Grad (für ungerade \(m\)) führt.Referenzen
[1]‘Mathieu function’. Wikipedia. https://en.wikipedia.org/wiki/Mathieu_function
Beispiele
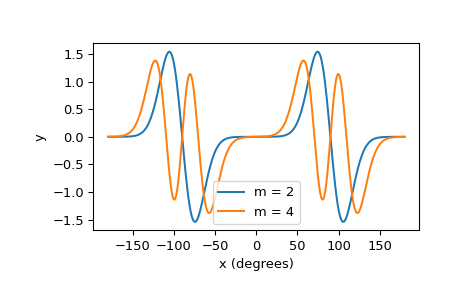
Plotten Sie ungerade Mathieufunktionen der Ordnungen
2und4.>>> import numpy as np >>> from scipy import special >>> import matplotlib.pyplot as plt >>> m = np.asarray([2, 4]) >>> q = 50 >>> x = np.linspace(-180, 180, 300)[:, np.newaxis] >>> y, _ = special.mathieu_sem(m, q, x) >>> plt.plot(x, y) >>> plt.xlabel('x (degrees)') >>> plt.ylabel('y') >>> plt.legend(('m = 2', 'm = 4'))
Da die Ordnungen
2und4gerade sind, beträgt die Periode jeder Funktion 180 Grad.