scipy.stats.

Gemisch#

class scipy.stats.Mixture(components, *, weights=None)[Quelle]#

Repräsentation einer Mischverteilung.

Eine Mischverteilung ist die Verteilung einer Zufallsvariablen, die auf folgende Weise definiert ist: Zuerst wird eine Zufallsvariable aus components gemäß der von weights gegebenen Wahrscheinlichkeiten ausgewählt, dann wird die ausgewählte Zufallsvariable realisiert.

Parameter:

componentsSequenz von ContinuousDistribution: Die zugrundeliegenden Instanzen von ContinuousDistribution. Alle müssen skalare Formparameter haben (falls vorhanden); z. B. muss die bei einem skalaren Argument ausgewertete pdf einen Skalar zurückgeben.
weightsSequenz von Gleitkommazahlen, optional: Die entsprechenden Wahrscheinlichkeiten für die Auswahl jeder Zufallsvariablen. Müssen nicht-negativ sein und sich zu eins summieren. Das Standardverhalten ist, alle Komponenten gleich zu gewichten.

Attribute:

componentsSequenz von ContinuousDistribution: Die zugrundeliegenden Instanzen von ContinuousDistribution.
weightsndarray: Die entsprechenden Wahrscheinlichkeiten für die Auswahl jeder Zufallsvariablen.

Methoden

`support`()	Unterstützungsbereich der Zufallsvariable
`sample`([shape, rng, method])	Zufällige Stichprobe aus der Verteilung.
`moment`([order, kind, method])	Roh-, zentrales oder Standardmoment positiver ganzzahliger Ordnung.
`mean`(*[, method])	Mittelwert (rohes erstes Moment um den Ursprung)
`median`(*[, method])	Median (50. Perzentil)
`mode`(*[, method])	Modus (wahrscheinlichster Wert)
`variance`(*[, method])	Varianz (zweites zentrales Moment)
`standard_deviation`(*[, method])	Standardabweichung (Quadratwurzel des zweiten zentralen Moments)
`skewness`(*[, method])	Schiefe (standardisiertes drittes Moment)
`kurtosis`(*[, method])	Kurtosis (standardisiertes viertes Moment)
`pdf`(x, /, *[, method])	Wahrscheinlichkeitsdichtefunktion
`logpdf`(x, /, *[, method])	Logarithmus der Wahrscheinlichkeitsdichtefunktion
`cdf`(x[, y, method])	Kumulative Verteilungsfunktion
`icdf`(p, /, *[, method])	Inverse der kumulativen Verteilungsfunktion.
`ccdf`(x[, y, method])	Komplementäre kumulative Verteilungsfunktion
`iccdf`(p, /, *[, method])	Inverse der komplementären kumulativen Verteilungsfunktion.
`logcdf`(x[, y, method])	Logarithmus der kumulativen Verteilungsfunktion
`ilogcdf`(p, /, *[, method])	Inverse des Logarithmus der kumulativen Verteilungsfunktion.
`logccdf`(x[, y, method])	Logarithmus der komplementären kumulativen Verteilungsfunktion
`ilogccdf`(p, /, *[, method])	Inverse des Logarithmus der komplementären kumulativen Verteilungsfunktion.
`entropy`(*[, method])	Differentielle Entropie

Hinweise

Die folgenden Abkürzungen werden im gesamten Dokument verwendet.

PDF: Wahrscheinlichkeitsdichtefunktion
CDF: Kumulative Verteilungsfunktion
CCDF: Komplementäre CDF
Entropie: Differentielle Entropie
Log-F: Logarithmus von F (z. B. Log-CDF)
Inverse F: Inverse Funktion von F (z. B. Inverse CDF)

Referenzen

[1]

Mischverteilung, Wikipedia, https://en.wikipedia.org/wiki/Mixture_distribution

Beispiele

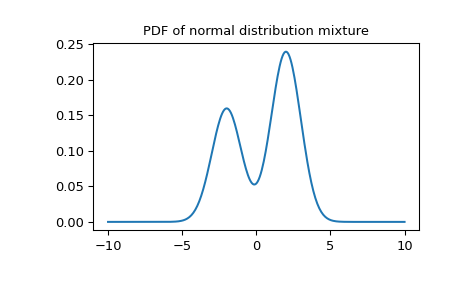
Ein Gemisch aus Normalverteilungen

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> X1 = stats.Normal(mu=-2, sigma=1)
>>> X2 = stats.Normal(mu=2, sigma=1)
>>> mixture = stats.Mixture([X1, X2], weights=[0.4, 0.6])
>>> print(f'mean: {mixture.mean():.2f}, '
...       f'median: {mixture.median():.2f}, '
...       f'mode: {mixture.mode():.2f}')
mean: 0.40, median: 1.04, mode: 2.00
>>> x = np.linspace(-10, 10, 300)
>>> plt.plot(x, mixture.pdf(x))
>>> plt.title('PDF of normal distribution mixture')
>>> plt.show()