scipy.stats.

boxcox_llf

scipy.stats.boxcox_llf(lmb, data, *, axis=0, keepdims=False, nan_policy='propagate')

Die Box-Cox-Log-Likelihood-Funktion.

Parameter:

lmbSkalar

Parameter für die Box-Cox-Transformation. Siehe boxcox für Details.

dataarray_like

Daten zur Berechnung der Box-Cox-Log-Likelihood. Wenn data mehrdimensional ist, wird die Log-Likelihood entlang der ersten Achse berechnet.

axisint, Standard: 0

Wenn es sich um eine ganze Zahl handelt, ist dies die Achse des Eingabearrays, entlang der die Statistik berechnet wird. Die Statistik jedes Achsen-Slices (z. B. Zeile) der Eingabe erscheint dann in einem entsprechenden Element der Ausgabe. Wenn None, wird die Eingabe vor der Berechnung der Statistik geglättet.

nan_policy{‘propagate’, ‘omit’, ‘raise’

Definiert, wie Eingabe-NaNs behandelt werden.

• propagate: Wenn ein NaN in der Achsen-Slice (z. B. Zeile) vorhanden ist, entlang der die Statistik berechnet wird, wird der entsprechende Eintrag der Ausgabe NaN sein.

• omit: NaNs werden bei der Berechnung weggelassen. Wenn im Achsen-Slice, entlang dem die Statistik berechnet wird, nicht genügend Daten verbleiben, wird der entsprechende Eintrag der Ausgabe NaN sein.

• raise: Wenn ein NaN vorhanden ist, wird ein ValueError ausgelöst.

keepdimsbool, Standard: False

Wenn dies auf True gesetzt ist, bleiben die reduzierten Achsen im Ergebnis als Dimensionen mit der Größe eins erhalten. Mit dieser Option wird das Ergebnis korrekt gegen das Eingabearray gestreut (broadcasted).

Rückgabe:

llffloat oder ndarray

Box-Cox-Log-Likelihood von data gegeben lmb. Ein Float für 1D data, sonst ein Array.

Siehe auch

boxcox, probplot, boxcox_normplot, boxcox_normmax

Hinweise

Die Box-Cox-Log-Likelihood-Funktion \(l\) ist hier definiert als

\[l = (\lambda - 1) \sum_i^N \log(x_i) - \frac{N}{2} \log\left(\sum_i^N (y_i - \bar{y})^2 / N\right),\]

wobei \(N\) die Anzahl der Datenpunkte data ist und \(y\) die Box-Cox-transformierten Eingangsdaten sind. Dies entspricht der Profil-Log-Likelihood der ursprünglichen Daten \(x\), wobei einige konstante Terme weggelassen wurden.

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.axes_grid1.inset_locator import inset_axes

Erzeugen Sie einige Zufallsvariablen und berechnen Sie die Box-Cox-Log-Likelihood-Werte für eine Reihe von lmbda-Werten.

>>> rng = np.random.default_rng()
>>> x = stats.loggamma.rvs(5, loc=10, size=1000, random_state=rng)
>>> lmbdas = np.linspace(-2, 10)
>>> llf = np.zeros(lmbdas.shape, dtype=float)
>>> for ii, lmbda in enumerate(lmbdas):
...     llf[ii] = stats.boxcox_llf(lmbda, x)

Finden Sie auch den optimalen lmbda-Wert mit boxcox.

>>> x_most_normal, lmbda_optimal = stats.boxcox(x)

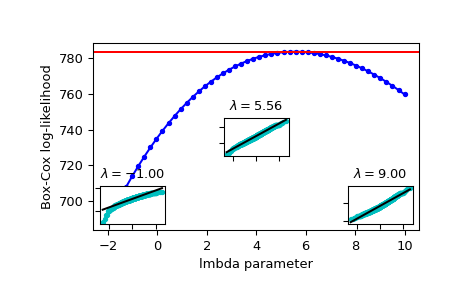
Plotten Sie die Log-Likelihood als Funktion von lmbda. Fügen Sie die optimale lmbda als horizontale Linie hinzu, um zu überprüfen, ob dies wirklich das Optimum ist.

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(lmbdas, llf, 'b.-')
>>> ax.axhline(stats.boxcox_llf(lmbda_optimal, x), color='r')
>>> ax.set_xlabel('lmbda parameter')
>>> ax.set_ylabel('Box-Cox log-likelihood')

Fügen Sie nun einige Wahrscheinlichkeitsplots hinzu, um zu zeigen, dass dort, wo die Log-Likelihood maximiert wird, die mit boxcox transformierten Daten am ehesten normal aussehen.

>>> locs = [3, 10, 4]  # 'lower left', 'center', 'lower right'
>>> for lmbda, loc in zip([-1, lmbda_optimal, 9], locs):
...     xt = stats.boxcox(x, lmbda=lmbda)
...     (osm, osr), (slope, intercept, r_sq) = stats.probplot(xt)
...     ax_inset = inset_axes(ax, width="20%", height="20%", loc=loc)
...     ax_inset.plot(osm, osr, 'c.', osm, slope*osm + intercept, 'k-')
...     ax_inset.set_xticklabels([])
...     ax_inset.set_yticklabels([])
...     ax_inset.set_title(r'$\lambda=%1.2f$' % lmbda)

>>> plt.show()

ZurückIn Tab öffnen