scipy.stats.

ecdf#

scipy.stats.ecdf(sample)[Quelle]#

Empirische kumulative Verteilungsfunktion einer Stichprobe.

Die empirische kumulative Verteilungsfunktion (ECDF) ist eine Stufenfunktion, die die CDF der Verteilung schätzt, die einer Stichprobe zugrunde liegt. Diese Funktion gibt Objekte zurück, die sowohl die empirische Verteilungsfunktion als auch deren Komplement, die empirische Überlebensfunktion, darstellen.

Parameter:

sample1D array_like oder scipy.stats.CensoredData: Neben array_like werden Instanzen von scipy.stats.CensoredData mit unzensierten und rechtszensierten Beobachtungen unterstützt. Derzeit führen andere Instanzen von scipy.stats.CensoredData zu einem NotImplementedError.

Rückgabe:

resECDFResult

Ein Objekt mit den folgenden Attributen.

cdfEmpiricalDistributionFunction: Ein Objekt, das die empirische kumulative Verteilungsfunktion darstellt.
sfEmpiricalDistributionFunction: Ein Objekt, das die empirische Überlebensfunktion darstellt.

Die Attribute cdf und sf selbst haben die folgenden Attribute.

quantilesndarray: Die eindeutigen Werte in der Stichprobe, die die empirische CDF/SF definieren.
probabilitiesndarray: Die Punktschätzungen der Wahrscheinlichkeiten, die den quantiles entsprechen.

Und die folgenden Methoden

evaluate(x): Bewerte die CDF/SF am Argument.
plot(ax): Zeichne die CDF/SF auf den bereitgestellten Achsen.
confidence_interval(confidence_level=0.95): Berechne das Konfidenzintervall um die CDF/SF für die Werte in quantiles.

Hinweise

Wenn jede Beobachtung der Stichprobe eine präzise Messung ist, springt die ECDF bei jeder der Beobachtungen um 1/len(sample) an [1].

Wenn Beobachtungen untere Grenzen, obere Grenzen oder beides sind, spricht man von „zensierten“ Daten, und sample kann als Instanz von scipy.stats.CensoredData übergeben werden.

Für rechtszensierte Daten wird die ECDF durch den Kaplan-Meier-Schätzer gegeben [2]; andere Formen der Zensierung werden derzeit nicht unterstützt.

Konfidenzintervalle werden nach der Greenwood-Formel oder der neueren „Exponential Greenwood“-Formel berechnet, wie in [4] beschrieben.

Referenzen

[1] (1,2,3)

Conover, William Jay. Practical nonparametric statistics. Vol. 350. John Wiley & Sons, 1999.

[2]

Kaplan, Edward L., and Paul Meier. “Nonparametric estimation from incomplete observations.” Journal of the American statistical association 53.282 (1958): 457-481.

[3]

Goel, Manish Kumar, Pardeep Khanna, and Jugal Kishore. “Understanding survival analysis: Kaplan-Meier estimate.” International journal of Ayurveda research 1.4 (2010): 274.

[4]

Sawyer, Stanley. “The Greenwood and Exponential Greenwood Confidence Intervals in Survival Analysis.” https://www.math.wustl.edu/~sawyer/handouts/greenwood.pdf

Beispiele

Unzensierte Daten

Wie im Beispiel aus [1] Seite 79 wurden fünf Jungen zufällig aus denen einer High School ausgewählt. Ihre Ein-Meilen-Laufzeiten wurden wie folgt aufgezeichnet.

>>> sample = [6.23, 5.58, 7.06, 6.42, 5.20]  # one-mile run times (minutes)

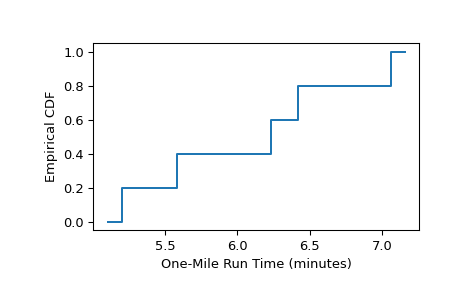
Die empirische Verteilungsfunktion, die die Verteilungsfunktion der Ein-Meilen-Laufzeiten der Population, aus der die Jungen stichprobenartig entnommen wurden, approximiert, wird wie folgt berechnet.

>>> from scipy import stats
>>> res = stats.ecdf(sample)
>>> res.cdf.quantiles
array([5.2 , 5.58, 6.23, 6.42, 7.06])
>>> res.cdf.probabilities
array([0.2, 0.4, 0.6, 0.8, 1. ])

Um das Ergebnis als Stufenfunktion darzustellen

>>> import matplotlib.pyplot as plt
>>> ax = plt.subplot()
>>> res.cdf.plot(ax)
>>> ax.set_xlabel('One-Mile Run Time (minutes)')
>>> ax.set_ylabel('Empirical CDF')
>>> plt.show()

../../_images/scipy-stats-ecdf-1_00_00.png

Rechtszensierte Daten

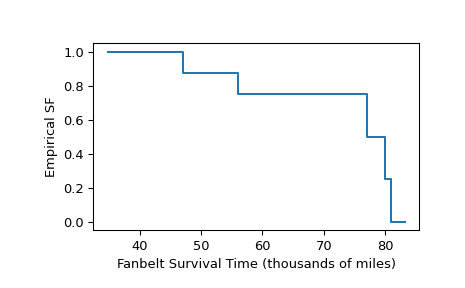
Wie im Beispiel aus [1] Seite 91 wurden die Lebensdauern von zehn Keilriemen getestet. Fünf Tests wurden abgebrochen, weil der getestete Keilriemen riss, aber die übrigen Tests aus anderen Gründen beendet wurden (z. B. die Studie hatte kein Geld mehr, aber der Keilriemen war noch funktionsfähig). Die mit den Keilriemen gefahrenen Kilometerstände wurden wie folgt aufgezeichnet.

>>> broken = [77, 47, 81, 56, 80]  # in thousands of miles driven
>>> unbroken = [62, 60, 43, 71, 37]

Die genauen Überlebenszeiten der Keilriemen, die am Ende der Tests noch funktionsfähig waren, sind unbekannt, aber sie übersteigen die in unbroken aufgezeichneten Werte. Daher sind diese Beobachtungen „rechtszensiert“, und die Daten werden mithilfe von scipy.stats.CensoredData dargestellt.

>>> sample = stats.CensoredData(uncensored=broken, right=unbroken)

Die empirische Überlebensfunktion wird wie folgt berechnet.

>>> res = stats.ecdf(sample)
>>> res.sf.quantiles
array([37., 43., 47., 56., 60., 62., 71., 77., 80., 81.])
>>> res.sf.probabilities
array([1.   , 1.   , 0.875, 0.75 , 0.75 , 0.75 , 0.75 , 0.5  , 0.25 , 0.   ])

Um das Ergebnis als Stufenfunktion darzustellen

>>> ax = plt.subplot()
>>> res.sf.plot(ax)
>>> ax.set_xlabel('Fanbelt Survival Time (thousands of miles)')
>>> ax.set_ylabel('Empirical SF')
>>> plt.show()

../../_images/scipy-stats-ecdf-1_01_00.png