goodness_of_fit#
- scipy.stats.goodness_of_fit(dist, data, *, known_params=None, fit_params=None, guessed_params=None, statistic='ad', n_mc_samples=9999, rng=None)[Quelle]#
Führt einen Anpassungstest durch, der Daten mit einer Verteilungsfamilie vergleicht.
Gegeben eine Verteilungsfamilie und Daten, führt die Funktion einen Test der Nullhypothese durch, dass die Daten aus einer Verteilung dieser Familie gezogen wurden. Bekannte Parameter der Verteilung können angegeben werden. Verbleibende Parameter der Verteilung werden an die Daten angepasst und der p-Wert des Tests wird entsprechend berechnet. Mehrere Statistiken zum Vergleich der Verteilung mit den Daten sind verfügbar.
- Parameter:
- dist
scipy.stats.rv_continuous Das Objekt, das die Verteilungsfamilie unter der Nullhypothese repräsentiert.
- data1D array_like
Endliche, nicht zensierte Daten, die getestet werden sollen.
- known_paramsdict, optional
Ein Wörterbuch mit Namen-Wert-Paaren bekannter Verteilungsparameter. Monte-Carlo-Stichproben werden zufällig aus der nullhypothetischen Verteilung mit diesen Parameterwerten gezogen. Bevor die Statistik für die beobachteten data und jede Monte-Carlo-Stichprobe ausgewertet wird, werden nur die verbleibenden unbekannten Parameter der nullhypothetischen Verteilungsfamilie an die Stichproben angepasst; die bekannten Parameter bleiben fest. Wenn alle Parameter der Verteilungsfamilie bekannt sind, wird der Schritt der Anpassung der Verteilungsfamilie an jede Stichprobe weggelassen.
- fit_paramsdict, optional
Ein Wörterbuch mit Namen-Wert-Paaren von Verteilungsparametern, die bereits an die Daten angepasst wurden, z.B. unter Verwendung von
scipy.stats.fitoder der Methodefitvon dist. Monte-Carlo-Stichproben werden aus der nullhypothetischen Verteilung mit diesen angegebenen Parameterwerten gezogen. Diese und alle anderen unbekannten Parameter der nullhypothetischen Verteilungsfamilie werden jedoch immer an die Stichprobe angepasst, sei es die beobachteten data oder eine Monte-Carlo-Stichprobe, bevor die Statistik ausgewertet wird.- guessed_paramsdict, optional
Ein Wörterbuch mit Namen-Wert-Paaren von Verteilungsparametern, die geschätzt wurden. Diese Parameter werden immer als freie Parameter betrachtet und sowohl an die bereitgestellten data als auch an die aus der nullhypothetischen Verteilung gezogenen Monte-Carlo-Stichproben angepasst. Der Zweck dieser guessed_params ist es, als Anfangswerte für das numerische Anpassungsverfahren zu dienen.
- statistic{“ad”, “ks”, “cvm”, “filliben”} oder aufrufbar, optional
Die Statistik, die verwendet wird, um Daten nach der Anpassung unbekannter Parameter der Verteilungsfamilie an die Daten mit einer Verteilung zu vergleichen. Die Statistiken Anderson-Darling (“ad”) [1], Kolmogorov-Smirnov (“ks”) [1], Cramer-von Mises (“cvm”) [1] und Filliben (“filliben”) [7] sind verfügbar. Alternativ kann eine aufrufbare Funktion mit der Signatur
(dist, data, axis)bereitgestellt werden, um die Statistik zu berechnen. Hier istdistein gefrorenes Verteilungsobjekt (möglicherweise mit Array-Parametern),dataist ein Array von Monte-Carlo-Stichproben (mit kompatibler Form) undaxisist die Achse vondata, entlang derer die Statistik berechnet werden muss.- n_mc_samplesint, Standard: 9999
Die Anzahl der Monte-Carlo-Stichproben, die aus der nullhypothetischen Verteilung gezogen werden, um die Nullverteilung der Statistik zu bilden. Die Stichprobengröße jeder ist die gleiche wie die der gegebenen data.
- rng{None, int,
numpy.random.Generator}, optional Wenn rng als Schlüsselwort übergeben wird, werden andere Typen als
numpy.random.Generatorannumpy.random.default_rngübergeben, um einenGeneratorzu instanziieren. Wenn rng bereits eineGenerator-Instanz ist, dann wird die bereitgestellte Instanz verwendet. Geben Sie rng für reproduzierbares Funktionsverhalten an.Wenn dieses Argument positional übergeben wird oder random_state als Schlüsselwort übergeben wird, gilt das ältere Verhalten für das Argument random_state.
Wenn random_state None ist (oder
numpy.random), wird die Singleton-Instanznumpy.random.RandomStateverwendet.Wenn random_state eine Ganzzahl ist, wird eine neue
RandomState-Instanz verwendet, die mit random_state initialisiert wurde.Wenn random_state bereits eine
Generator- oderRandomState-Instanz ist, wird diese Instanz verwendet.
Geändert in Version 1.15.0: Als Teil des SPEC-007-Übergangs von der Verwendung von
numpy.random.RandomStatezunumpy.random.Generatorwurde dieses Schlüsselwort von random_state zu rng geändert. Für einen Übergangszeitraum funktionieren beide Schlüsselwörter weiterhin, obwohl nur eines gleichzeitig angegeben werden kann. Nach dem Übergangszeitraum werden Funktionsaufrufe mit dem Schlüsselwort random_state Warnungen ausgeben. Das Verhalten von sowohl random_state als auch rng ist oben beschrieben, aber nur das Schlüsselwort rng sollte in neuem Code verwendet werden.
- dist
- Rückgabe:
- resGoodnessOfFitResult
Ein Objekt mit den folgenden Attributen.
- fit_result
FitResult Ein Objekt, das die Anpassung der bereitgestellten dist an data repräsentiert. Dieses Objekt enthält die Werte der Verteilungsfamilienparameter, die die nullhypothetische Verteilung vollständig definieren, d.h. die Verteilung, aus der Monte-Carlo-Stichproben gezogen werden.
- statisticfloat
Der Wert der Statistik, der die bereitgestellten data mit der nullhypothetischen Verteilung vergleicht.
- pvaluefloat
Der Anteil der Elemente in der Nullverteilung mit Statistikwerten, die mindestens so extrem sind wie der Statistikwert der bereitgestellten data.
- null_distributionndarray
Der Wert der Statistik für jede Monte-Carlo-Stichprobe, die aus der nullhypothetischen Verteilung gezogen wurde.
- fit_result
Hinweise
Dies ist ein generalisiertes Monte-Carlo-Verfahren für Anpassungstests, dessen Spezialfälle mit verschiedenen Anderson-Darling-Tests, dem Lilliefors-Test usw. übereinstimmen. Der Test wird in [2], [3] und [4] als parametrischer Bootstrap-Test beschrieben. Dies ist ein Monte-Carlo-Test, bei dem die Parameter, die die Verteilung spezifizieren, aus der Stichprobe geschätzt wurden. Wir beschreiben den Test durchweg mit „Monte Carlo“ anstelle von „parametrischem Bootstrap“, um Verwechslungen mit dem bekannteren nichtparametrischen Bootstrap zu vermeiden, und beschreiben unten, wie der Test durchgeführt wird.
Traditionelle Anpassungstests
Traditionell werden kritische Werte, die mit einem festen Satz von Signifikanzniveaus übereinstimmen, mithilfe von Monte-Carlo-Methoden vorausberechnet. Benutzer führen den Test durch, indem sie den Wert der Teststatistik nur für ihre beobachteten data berechnen und diesen Wert mit tabellierten kritischen Werten vergleichen. Diese Praxis ist nicht sehr flexibel, da Tabellen nicht für alle Verteilungen und Kombinationen von bekannten und unbekannten Parameterwerten verfügbar sind. Auch können die Ergebnisse ungenau sein, wenn kritische Werte aus begrenzten tabellierten Daten interpoliert werden, um mit der Stichprobengröße und den angepassten Parameterwerten des Benutzers übereinzustimmen. Um diese Mängel zu überwinden, ermöglicht diese Funktion dem Benutzer, die Monte-Carlo-Versuche an seine spezifischen Daten anzupassen.
Algorithmusübersicht
Kurz gesagt, diese Routine führt die folgenden Schritte aus:
Passen Sie unbekannte Parameter an die gegebenen data an, wodurch die „nullhypothetische“ Verteilung gebildet wird, und berechnen Sie die Statistik dieses Paares von Daten und Verteilung.
Ziehen Sie Zufallsstichproben aus dieser nullhypothetischen Verteilung.
Passen Sie die unbekannten Parameter an jede Zufallsstichprobe an.
Berechnen Sie die Statistik zwischen jeder Stichprobe und der an die Stichprobe angepassten Verteilung.
Vergleichen Sie den Wert der Statistik, der den data entspricht (1), mit den Werten der Statistik, die den Zufallsstichproben entsprechen (4). Der p-Wert ist der Anteil der Stichproben mit einem Statistikwert, der größer oder gleich dem Statistikwert der beobachteten Daten ist.
Im Detail sind die Schritte wie folgt:
Zuerst werden alle unbekannten Parameter der durch dist spezifizierten Verteilungsfamilie mithilfe der Maximum-Likelihood-Schätzung an die bereitgestellten data angepasst. (Eine Ausnahme ist die Normalverteilung mit unbekannter Lage und Skala: wir verwenden die bias-korrigierte Standardabweichung
np.std(data, ddof=1)für die Skala, wie in [1] empfohlen.) Diese Parameterwerte spezifizieren ein bestimmtes Mitglied der Verteilungsfamilie, das als „nullhypothetische Verteilung“ bezeichnet wird, d.h. die Verteilung, aus der die Daten unter der Nullhypothese gezogen wurden. Die statistic, die Daten mit einer Verteilung vergleicht, wird zwischen data und der nullhypothetischen Verteilung berechnet.Als nächstes werden viele (spezifisch n_mc_samples) neue Stichproben, die jeweils die gleiche Anzahl von Beobachtungen wie data enthalten, aus der nullhypothetischen Verteilung gezogen. Alle unbekannten Parameter der Verteilungsfamilie dist werden an *jede Resample* angepasst, und die statistic wird zwischen jeder Stichprobe und ihrer entsprechenden angepassten Verteilung berechnet. Diese Werte der Statistik bilden die Monte-Carlo-Nullverteilung (nicht zu verwechseln mit der oben genannten „nullhypothetischen Verteilung“).
Der p-Wert des Tests ist der Anteil der Statistikwerte in der Monte-Carlo-Nullverteilung, die mindestens so extrem sind wie der für data berechnete Statistikwert. Genauer gesagt, der p-Wert ist gegeben durch
\[p = \frac{b + 1} {m + 1}\]wobei \(b\) die Anzahl der Statistikwerte in der Monte-Carlo-Nullverteilung ist, die größer oder gleich dem für data berechneten Statistikwert sind, und \(m\) die Anzahl der Elemente in der Monte-Carlo-Nullverteilung (n_mc_samples) ist. Die Addition von \(1\) zum Zähler und Nenner kann als Einbeziehung des Werts der Statistik, der mit data übereinstimmt, in die Nullverteilung betrachtet werden, eine formalere Erklärung findet sich jedoch in [5].
Einschränkungen
Der Test kann für einige Verteilungsfamilien sehr langsam sein, da unbekannte Parameter der Verteilungsfamilie an jede der Monte-Carlo-Stichproben angepasst werden müssen und für die meisten Verteilungen in SciPy die Anpassung der Verteilung durch numerische Optimierung erfolgt.
Anti-Muster
Aus diesem Grund kann es verlockend sein, Parameter der Verteilung, die bereits von data angepasst wurden (vom Benutzer), so zu behandeln, als wären sie known_params, da die Angabe aller Parameter der Verteilung die Notwendigkeit, die Verteilung an jede Monte-Carlo-Stichprobe anzupassen, entfällt. (Dies ist im Wesentlichen die Art und Weise, wie der ursprüngliche Kilmogorov-Smirnov-Test durchgeführt wird.) Obwohl ein solcher Test Evidenz gegen die Nullhypothese liefern kann, ist der Test konservativ in dem Sinne, dass kleine p-Werte dazu neigen, die Wahrscheinlichkeit eines Typ-I-Fehlers (d.h. die Ablehnung der Nullhypothese, obwohl sie wahr ist) stark zu *überschätzen*, und die Aussagekraft des Tests gering ist (d.h. es ist unwahrscheinlicher, die Nullhypothese abzulehnen, selbst wenn die Nullhypothese falsch ist). Dies liegt daran, dass die Monte-Carlo-Stichproben weniger wahrscheinlich mit der nullhypothetischen Verteilung sowie mit data übereinstimmen. Dies neigt dazu, die Werte der Statistik, die in der Nullverteilung aufgezeichnet werden, zu erhöhen, so dass eine größere Anzahl davon den Wert der Statistik für data überschreitet, wodurch der p-Wert aufgebläht wird.
Referenzen
[1] (1,2,3,4,5)M. A. Stephens (1974). „EDF Statistics for Goodness of Fit and Some Comparisons.“ Journal of the American Statistical Association, Vol. 69, pp. 730-737.
[2]W. Stute, W. G. Manteiga und M. P. Quindimil (1993). „Bootstrap based goodness-of-fit-tests.“ Metrika 40.1: 243-256.
[3]C. Genest, & B Rémillard. (2008). „Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models.“ Annales de l’IHP Probabilités et statistiques. Vol. 44. No. 6.
[4]I. Kojadinovic und J. Yan (2012). „Goodness-of-fit testing based on a weighted bootstrap: A fast large-sample alternative to the parametric bootstrap.“ Canadian Journal of Statistics 40.3: 480-500.
[5]B. Phipson und G. K. Smyth (2010). „Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.“ Statistical Applications in Genetics and Molecular Biology 9.1.
[6]H. W. Lilliefors (1967). „On the Kolmogorov-Smirnov test for normality with mean and variance unknown.“ Journal of the American statistical Association 62.318: 399-402.
[7]Filliben, James J. „The probability plot correlation coefficient test for normality.“ Technometrics 17.1 (1975): 111-117.
Beispiele
Ein bekannter Test der Nullhypothese, dass Daten aus einer gegebenen Verteilung gezogen wurden, ist der Kolmogorov-Smirnov (KS)-Test, der in SciPy als
scipy.stats.ks_1sampverfügbar ist. Angenommen, wir wollen testen, ob die folgenden Daten>>> import numpy as np >>> from scipy import stats >>> rng = np.random.default_rng() >>> x = stats.uniform.rvs(size=75, random_state=rng)
aus einer Normalverteilung gezogen wurden. Um einen KS-Test durchzuführen, wird die empirische Verteilungsfunktion der beobachteten Daten mit der (theoretischen) kumulativen Verteilungsfunktion einer Normalverteilung verglichen. Um dies zu tun, muss natürlich die Normalverteilung unter der Nullhypothese vollständig spezifiziert sein. Dies geschieht üblicherweise, indem zunächst die Parameter
locundscaleder Verteilung an die beobachteten Daten angepasst werden und dann der Test durchgeführt wird.>>> loc, scale = np.mean(x), np.std(x, ddof=1) >>> cdf = stats.norm(loc, scale).cdf >>> stats.ks_1samp(x, cdf) KstestResult(statistic=0.1119257570456813, pvalue=0.2827756409939257, statistic_location=0.7751845155861765, statistic_sign=-1)
Ein Vorteil des KS-Tests ist, dass der p-Wert – die Wahrscheinlichkeit, unter der Nullhypothese einen Wert der Teststatistik zu erhalten, der so extrem ist wie der Wert, der aus den beobachteten Daten erhalten wurde – exakt und effizient berechnet werden kann.
goodness_of_fitkann diese Ergebnisse nur annähern.>>> known_params = {'loc': loc, 'scale': scale} >>> res = stats.goodness_of_fit(stats.norm, x, known_params=known_params, ... statistic='ks', rng=rng) >>> res.statistic, res.pvalue (0.1119257570456813, 0.2788)
Die Statistik stimmt exakt überein, aber der p-Wert wird geschätzt, indem eine „Monte-Carlo-Nullverteilung“ gebildet wird, d.h. indem explizit Zufallsstichproben aus
scipy.stats.normmit den angegebenen Parametern gezogen und die Statistik für jede berechnet wird. Der Anteil dieser Statistikwerte, die mindestens so extrem sind wieres.statistic, nähert den exakten p-Wert an, der vonscipy.stats.ks_1sampberechnet wird.In vielen Fällen ziehen wir es jedoch vor, nur zu testen, ob die Daten aus einem beliebigen Mitglied der Normalverteilungsfamilie stammen, nicht speziell aus der Normalverteilung mit der an die beobachtete Stichprobe angepassten Lage und Skala. In diesem Fall argumentierte Lilliefors [6], dass der KS-Test viel zu konservativ ist (d.h. der p-Wert überschätzt die tatsächliche Wahrscheinlichkeit, eine wahre Nullhypothese abzulehnen) und daher die Aussagekraft mangelt – die Fähigkeit, die Nullhypothese abzulehnen, wenn die Nullhypothese tatsächlich falsch ist. Tatsächlich ist unser p-Wert oben ungefähr 0,28, was viel zu groß ist, um die Nullhypothese auf jedem gängigen Signifikanzniveau abzulehnen.
Betrachten wir, warum das so sein könnte. Beachten Sie, dass in dem obigen KS-Test die Statistik immer Daten gegen die kumulative Verteilungsfunktion einer Normalverteilung vergleicht, die an die *beobachteten Daten* angepasst wurde. Dies tendiert dazu, den Wert der Statistik für die beobachteten Daten zu verringern, ist aber „unfair“, wenn die Statistik für andere Stichproben berechnet wird, wie z.B. diejenigen, die wir zufällig ziehen, um die Monte-Carlo-Nullverteilung zu bilden. Es ist einfach, dies zu korrigieren: Wann immer wir die KS-Statistik einer Stichprobe berechnen, verwenden wir die kumulative Verteilungsfunktion einer Normalverteilung, die an *diese Stichprobe* angepasst wurde. Die Nullverteilung ist in diesem Fall nicht exakt berechnet und wird typischerweise mittels Monte-Carlo-Methoden, wie oben beschrieben, angenähert. Hier glänzt
goodness_of_fit.>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ks', ... rng=rng) >>> res.statistic, res.pvalue (0.1119257570456813, 0.0196)
Tatsächlich ist dieser p-Wert viel kleiner und klein genug, um die Nullhypothese korrekt auf gängigen Signifikanzniveaus, einschließlich 5% und 2,5%, abzulehnen.
Die KS-Statistik ist jedoch nicht sehr empfindlich für alle Abweichungen von der Normalität. Der ursprüngliche Vorteil der KS-Statistik war die Möglichkeit, die Nullverteilung theoretisch zu berechnen, aber eine empfindlichere Statistik – die zu einer höheren Testaussagekraft führt – kann nun verwendet werden, da wir die Nullverteilung rechnerisch annähern können. Die Anderson-Darling-Statistik [1] ist tendenziell empfindlicher, und die kritischen Werte dieser Statistik wurden für verschiedene Signifikanzniveaus und Stichprobengrößen mithilfe von Monte-Carlo-Methoden tabelliert.
>>> res = stats.anderson(x, 'norm') >>> print(res.statistic) 1.2139573337497467 >>> print(res.critical_values) [0.549 0.625 0.75 0.875 1.041] >>> print(res.significance_level) [15. 10. 5. 2.5 1. ]
Hier überschreitet der beobachtete Wert der Statistik den kritischen Wert, der einem Signifikanzniveau von 1% entspricht. Dies sagt uns, dass der p-Wert der beobachteten Daten kleiner als 1% ist, aber was ist er? Wir könnten aus diesen (bereits interpolierten) Werten interpolieren, aber
goodness_of_fitkann ihn direkt schätzen.>>> res = stats.goodness_of_fit(stats.norm, x, statistic='ad', ... rng=rng) >>> res.statistic, res.pvalue (1.2139573337497467, 0.0034)
Ein weiterer Vorteil ist, dass die Verwendung von
goodness_of_fitnicht auf eine bestimmte Menge von Verteilungen oder Bedingungen beschränkt ist, welche Parameter bekannt sind und welche aus Daten geschätzt werden müssen. Stattdessen kanngoodness_of_fitp-Werte relativ schnell für jede Verteilung mit einer ausreichend schnellen und zuverlässigenfit-Methode schätzen. Zum Beispiel führen wir hier einen Anpassungstest mit der Cramer-von-Mises-Statistik gegen die Rayleigh-Verteilung mit bekannter Lage und unbekannter Skala durch.>>> rng = np.random.default_rng() >>> x = stats.chi(df=2.2, loc=0, scale=2).rvs(size=1000, random_state=rng) >>> res = stats.goodness_of_fit(stats.rayleigh, x, statistic='cvm', ... known_params={'loc': 0}, rng=rng)
Dies wird ziemlich schnell ausgeführt, aber um die Zuverlässigkeit der
fit-Methode zu überprüfen, sollten wir das Anpassungsergebnis überprüfen.>>> res.fit_result # location is as specified, and scale is reasonable params: FitParams(loc=0.0, scale=2.1026719844231243) success: True message: 'The fit was performed successfully.' >>> import matplotlib.pyplot as plt # matplotlib must be installed to plot >>> res.fit_result.plot() >>> plt.show()
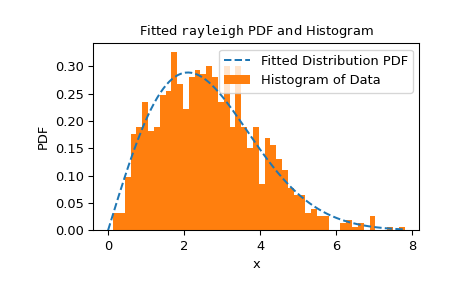
Wenn die Verteilung nicht so gut wie möglich an die beobachteten Daten angepasst ist, kontrolliert der Test möglicherweise nicht die Irrtumswahrscheinlichkeit, d.h. die Chance, die Nullhypothese abzulehnen, auch wenn sie wahr ist.
Wir sollten auch nach extremen Ausreißern in der Nullverteilung suchen, die durch unzuverlässige Anpassungen verursacht werden können. Diese machen das Ergebnis nicht unbedingt ungültig, verringern aber tendenziell die Aussagekraft des Tests.
>>> _, ax = plt.subplots() >>> ax.hist(np.log10(res.null_distribution)) >>> ax.set_xlabel("log10 of CVM statistic under the null hypothesis") >>> ax.set_ylabel("Frequency") >>> ax.set_title("Histogram of the Monte Carlo null distribution") >>> plt.show()
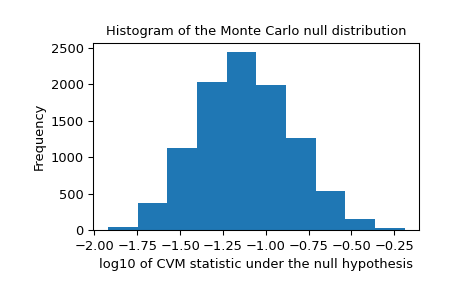
Diese Grafik erscheint beruhigend.
Wenn die
fit-Methode zuverlässig funktioniert und die Verteilung der Teststatistik nicht besonders empfindlich auf die Werte der angepassten Parameter reagiert, dann ist der vongoodness_of_fitbereitgestellte p-Wert eine gute Annäherung.>>> res.statistic, res.pvalue (0.2231991510248692, 0.0525)