scipy.stats.

kurtosis

scipy.stats.kurtosis(a, axis=0, fisher=True, bias=True, nan_policy='propagate', *, keepdims=False)

Berechnet die Kurtosis (Fisher oder Pearson) eines Datensatzes.

Die Kurtosis ist das vierte zentrale Moment geteilt durch das Quadrat der Varianz. Wenn Fishers Definition verwendet wird, wird von dem Ergebnis 3,0 subtrahiert, um 0,0 für eine Normalverteilung zu erhalten.

Wenn bias False ist, wird die Kurtosis mithilfe von k-Statistiken berechnet, um Verzerrungen durch verzerrte Momentenschätzer zu eliminieren.

Verwenden Sie kurtosistest, um zu prüfen, ob das Ergebnis nahe genug an einer Normalverteilung liegt.

Parameter:

aArray

Daten, für die die Kurtosis berechnet wird.

axisint oder None, Standard: 0

Wenn es sich um eine ganze Zahl handelt, ist dies die Achse des Eingabearrays, entlang der die Statistik berechnet wird. Die Statistik jedes Achsen-Slices (z. B. Zeile) der Eingabe erscheint dann in einem entsprechenden Element der Ausgabe. Wenn None, wird die Eingabe vor der Berechnung der Statistik geglättet.

fisherbool, optional

Wenn True, wird Fishers Definition verwendet (Normal ==> 0.0). Wenn False, wird Pearsons Definition verwendet (Normal ==> 3.0).

biasbool, optional

Wenn False, werden die Berechnungen zur Eliminierung statistischer Verzerrungen korrigiert.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Definiert, wie Eingabe-NaNs behandelt werden.

• propagate: Wenn ein NaN in der Achsen-Slice (z. B. Zeile) vorhanden ist, entlang der die Statistik berechnet wird, wird der entsprechende Eintrag der Ausgabe NaN sein.

• omit: NaNs werden bei der Berechnung weggelassen. Wenn im Achsen-Slice, entlang dem die Statistik berechnet wird, nicht genügend Daten verbleiben, wird der entsprechende Eintrag der Ausgabe NaN sein.

• raise: Wenn ein NaN vorhanden ist, wird ein ValueError ausgelöst.

keepdimsbool, Standard: False

Wenn dies auf True gesetzt ist, bleiben die reduzierten Achsen im Ergebnis als Dimensionen mit der Größe eins erhalten. Mit dieser Option wird das Ergebnis korrekt gegen das Eingabearray gestreut (broadcasted).

Rückgabe:

kurtosisarray

Die Kurtosis der Werte entlang einer Achse, wobei NaN zurückgegeben wird, wenn alle Werte gleich sind.

Hinweise

Seit SciPy 1.9 werden np.matrix-Eingaben (für neuen Code nicht empfohlen) vor der Berechnung in np.ndarray konvertiert. In diesem Fall ist die Ausgabe eine Skalar- oder np.ndarray mit geeigneter Form anstelle eines 2D-np.matrix. Ebenso werden, während maskierte Elemente von Masked Arrays ignoriert werden, die Ausgabe eine Skalar- oder np.ndarray anstelle eines Masked Arrays mit mask=False sein.

kurtosis unterstützt experimentell Python Array API Standard-kompatible Backends zusätzlich zu NumPy. Bitte erwägen Sie, diese Funktionen zu testen, indem Sie eine Umgebungsvariable SCIPY_ARRAY_API=1 setzen und CuPy, PyTorch, JAX oder Dask-Arrays als Array-Argumente übergeben. Die folgenden Kombinationen von Backend und Gerät (oder anderer Fähigkeit) werden unterstützt.

Bibliothek	CPU	GPU
NumPy	✅	n/a
CuPy	n/a	✅
PyTorch	✅	✅
JAX	⚠️ kein JIT	⚠️ kein JIT
Dask	⚠️ berechnet Graph	n/a

Siehe Unterstützung für den Array API Standard für weitere Informationen.

Referenzen

[1]

Zwillinger, D. und Kokoska, S. (2000). CRC Standard Probability and Statistics Tables and Formulae. Chapman & Hall: New York. 2000.

Beispiele

Probieren Sie es in Ihrem Browser aus!

In Fishers Definition ist die Kurtosis der Normalverteilung null. Im folgenden Beispiel ist die Kurtosis nahe null, da sie aus dem Datensatz und nicht aus der kontinuierlichen Verteilung berechnet wurde.

>>> import numpy as np
>>> from scipy.stats import norm, kurtosis
>>> data = norm.rvs(size=1000, random_state=3)
>>> kurtosis(data)
-0.06928694200380558

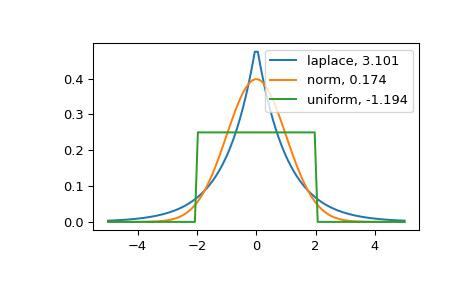
Die Verteilung mit höherer Kurtosis hat einen schwereren Schwanz. Die Kurtosis Null der Normalverteilung in Fishers Definition kann als Referenzpunkt dienen.

>>> import matplotlib.pyplot as plt
>>> import scipy.stats as stats
>>> from scipy.stats import kurtosis

>>> x = np.linspace(-5, 5, 100)
>>> ax = plt.subplot()
>>> distnames = ['laplace', 'norm', 'uniform']

>>> for distname in distnames:
...     if distname == 'uniform':
...         dist = getattr(stats, distname)(loc=-2, scale=4)
...     else:
...         dist = getattr(stats, distname)
...     data = dist.rvs(size=1000)
...     kur = kurtosis(data, fisher=True)
...     y = dist.pdf(x)
...     ax.plot(x, y, label="{}, {}".format(distname, round(kur, 3)))
...     ax.legend()

Die Laplace-Verteilung hat einen schwereren Schwanz als die Normalverteilung. Die Gleichverteilung (die eine negative Kurtosis hat) hat den dünnsten Schwanz.

ZurückIn Tab öffnen