scipy.stats.multivariate_t

scipy.stats.multivariate_t = <scipy.stats._multivariate.multivariate_t_gen object>

Eine multivariate t-verteilte Zufallsvariable.

Der Parameter loc gibt die Lage an. Der Parameter shape gibt die positiv semidefinierte Formmatrix an. Der Parameter df gibt die Freiheitsgrade an.

Zusätzlich zum Aufrufen der unten aufgeführten Methoden kann das Objekt selbst als Funktion aufgerufen werden, um die Parameter für Lage, Formmatrix und Freiheitsgrade festzulegen und eine „eingefrorene“ multivariate t-Verteilungszufallsvariable zurückzugeben.

Parameter:

locarray_like, optional

Lage der Verteilung. (Standard: 0)

shapearray_like, optional

Positiv semidefinierte Matrix der Verteilung. (Standard: 1)

dffloat, optional

Freiheitsgrade der Verteilung; muss größer als Null sein. Wenn np.inf, dann sind die Ergebnisse multivariat normal. Der Standardwert ist 1.

allow_singularbool, optional

Ob eine singuläre Matrix zugelassen werden soll. (Standard: False)

seed{None, int, np.random.RandomState, np.random.Generator}, optional

Wird zum Ziehen von Zufallsvarianten verwendet. Wenn seed None ist, wird die RandomState Singleton verwendet. Wenn seed eine Ganzzahl ist, wird eine neue RandomState-Instanz verwendet, die mit seed initialisiert wird. Wenn seed bereits eine RandomState- oder Generator-Instanz ist, wird dieses Objekt verwendet. Standard ist None.

Methoden

pdf(x, loc=None, shape=1, df=1, allow_singular=False)	Wahrscheinlichkeitsdichtefunktion.
logpdf(x, loc=None, shape=1, df=1, allow_singular=False)	Logarithmus der Wahrscheinlichkeitsdichtefunktion.
cdf(x, loc=None, shape=1, df=1, allow_singular=False, *,	maxpts=None, lower_limit=None, random_state=None) Kumulative Verteilungsfunktion.
rvs(loc=None, shape=1, df=1, size=1, random_state=None)	Ziehe zufällige Stichproben aus einer multivariaten t-Verteilung.
entropy(loc=None, shape=1, df=1)	Differenzielle Entropie einer multivariaten t-Verteilung.

Hinweise

Das Setzen des Parameters loc auf None ist äquivalent zum Nullvektor für loc. Der Parameter shape kann ein Skalar sein, in diesem Fall ist die Formmatrix die Identitätsmatrix multipliziert mit diesem Wert, ein Vektor von Diagonaleinträgen für die Formmatrix oder ein zweidimensionales array_like. Die Matrix shape muss eine (symmetrische) positiv semidefinierte Matrix sein. Die Determinante und die Inverse von shape werden als Pseudo-Determinante und Pseudo-Inverse berechnet, sodass shape keinen vollen Rang haben muss.

Die Wahrscheinlichkeitsdichtefunktion für multivariate_t ist

\[f(x) = \frac{\Gamma((\nu + p)/2)}{\Gamma(\nu/2)\nu^{p/2}\pi^{p/2}|\Sigma|^{1/2}} \left[1 + \frac{1}{\nu} (\mathbf{x} - \boldsymbol{\mu})^{\top} \boldsymbol{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu}) \right]^{-(\nu + p)/2},\]

wobei \(p\) die Dimension von \(\mathbf{x}\) ist, \(\boldsymbol{\mu}\) der \(p\)-dimensionale Ort ist, \(\boldsymbol{\Sigma}\) die \(p \times p\)-dimensionale Formmatrix und \(\nu\) die Freiheitsgrade sind.

Hinzugefügt in Version 1.6.0.

Referenzen

[1]

Arellano-Valle et al. „Shannon Entropy and Mutual Information for Multivariate Skew-Elliptical Distributions“. Scandinavian Journal of Statistics. Bd. 40, Ausgabe 1.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Das Objekt kann (als Funktion) aufgerufen werden, um die Parameter loc, shape, df und allow_singular festzulegen, und gibt eine „eingefrorene“ multivariate_t Zufallsvariable zurück.

>>> import numpy as np
>>> from scipy.stats import multivariate_t
>>> rv = multivariate_t([1.0, -0.5], [[2.1, 0.3], [0.3, 1.5]], df=2)
>>> # Frozen object with the same methods but holding the given location,
>>> # scale, and degrees of freedom fixed.

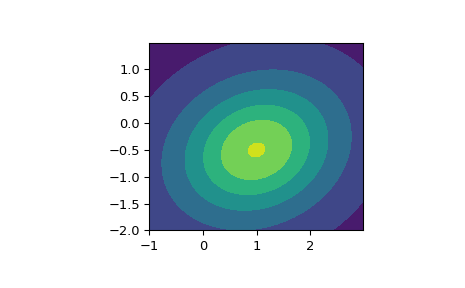
Erstellt ein Konturdiagramm der PDF.

>>> import matplotlib.pyplot as plt
>>> x, y = np.mgrid[-1:3:.01, -2:1.5:.01]
>>> pos = np.dstack((x, y))
>>> fig, ax = plt.subplots(1, 1)
>>> ax.set_aspect('equal')
>>> plt.contourf(x, y, rv.pdf(pos))

ZurückIn Tab öffnen