scipy.stats.qmc.

PoissonDisk#

class scipy.stats.qmc.PoissonDisk(d, *, radius=0.05, hypersphere='volume', ncandidates=30, optimization=None, rng=None, l_bounds=None, u_bounds=None)[Quelle]#

Poisson-Scheiben-Sampling.

Parameter:
dint

Dimension des Parameterraums.

radiusfloat

Minimaler Abstand, der zwischen Punkten gehalten werden soll, wenn neue Kandidaten abgetastet werden.

hypersphere{“volume”, “surface”}, optional

Sampling-Strategie zur Erzeugung potenzieller Kandidaten, die in die endgültige Stichprobe aufgenommen werden sollen. Standard ist „volume“.

  • volume: Ursprünglicher Bridson-Algorithmus wie in [1] beschrieben. Neue Kandidaten werden *innerhalb* der Hypersphäre abgetastet.

  • surface: Nur die Oberfläche der Hypersphäre abtasten.

ncandidatesint

Anzahl der pro Iteration abzutastenden Kandidaten. Mehr Kandidaten führen zu einer dichteren Abtastung, da mehr Kandidaten pro Iteration akzeptiert werden können.

optimization{None, “random-cd”, “lloyd”}, optional

Ob ein Optimierungsschema zur Verbesserung der Qualität nach dem Sampling verwendet werden soll. Beachten Sie, dass dies ein Nachbearbeitungsschritt ist, der nicht garantiert, dass alle Eigenschaften der Stichprobe erhalten bleiben. Standard ist None.

  • random-cd: zufällige Permutationen von Koordinaten zur Verringerung der zentrierten Diskrepanz. Die beste Stichprobe basierend auf der zentrierten Diskrepanz wird ständig aktualisiert. Das zentrierte dispunktbasierte Sampling zeigt eine bessere Raumfüllungsrobustheit gegenüber 2D- und 3D-Unterprojektionen im Vergleich zur Verwendung anderer Dispunktmaße.

  • lloyd: Stört Stichproben mithilfe eines modifizierten Lloyd-Max-Algorithmus. Der Prozess konvergiert zu gleichmäßig verteilten Stichproben.

Hinzugefügt in Version 1.10.0.

rngnumpy.random.Generator, optional

Zustand des pseudozufälligen Zahlengenerators. Wenn rng None ist, wird ein neuer numpy.random.Generator mithilfe der Entropie des Betriebssystems erstellt. Typen außer numpy.random.Generator werden an numpy.random.default_rng übergeben, um einen Generator zu instanziieren.

Geändert in Version 1.15.0: Als Teil des SPEC-007-Übergangs von der Verwendung von numpy.random.RandomState zu numpy.random.Generator wurde dieses Schlüsselwort von seed in rng geändert. Für eine Übergangszeit funktionieren beide Schlüsselwörter weiterhin, obwohl nur eines gleichzeitig angegeben werden darf. Nach der Übergangszeit geben Funktionsaufrufe mit dem Schlüsselwort seed Warnungen aus. Nach einer Deprekationsfrist wird das Schlüsselwort seed entfernt.

l_bounds, u_boundsarray_like (d,)

Untere und obere Grenzen der Ziel-Stichprobendaten.

Methoden

fast_forward(n)

Führt die Sequenz um n Positionen vorwärts.

fill_space()

Zeichne n Stichproben im Intervall [l_bounds, u_bounds].

integers(l_bounds, *[, u_bounds, n, ...])

Zieht n ganze Zahlen von l_bounds (inklusive) bis u_bounds (exklusive), oder wenn endpoint=True, von l_bounds (inklusive) bis u_bounds (inklusive).

random([n, workers])

Zieht n im halboffenen Intervall [0, 1).

reset()

Setzt die Engine auf den Grundzustand zurück.

Hinweise

Das Poisson-Scheiben-Sampling ist eine iterative Sampling-Strategie. Beginnend mit einer Startstichprobe werden ncandidates in der Hypersphäre um den Startpunkt abgetastet. Kandidaten, die unterhalb eines bestimmten radius liegen oder außerhalb des Bereichs, werden abgelehnt. Neue Stichproben werden in einem Pool von Stichproben-Startpunkten hinzugefügt. Der Prozess stoppt, wenn der Pool leer ist oder wenn die Anzahl der benötigten Stichproben erreicht ist.

Die maximale Anzahl von Punkten, die eine Stichprobe enthalten kann, ist direkt mit dem radius verknüpft. Wenn die Dimension des Raumes zunimmt, breitet ein höherer Radius die Punkte weiter aus und hilft, den Fluch der Dimensionalität zu überwinden. Weitere Informationen finden Sie im Tutorial zu Quasi-Monte-Carlo.

Warnung

Der Algorithmus eignet sich aufgrund seiner iterativen Natur und seines Speicherbedarfs besser für niedrige Dimensionen und Stichprobengrößen. Die Wahl eines kleinen Radius bei hoher Dimension bedeutet, dass der Raum mehr Stichproben enthalten könnte als bei niedrigeren Dimensionen oder einem größeren Radius.

Einige Codefragmente wurden von [2] übernommen, der am 31.03.2021 von dem ursprünglichen Autor Shamis schriftlich zur kostenlosen Nutzung in SciPy unter der 3-Klausel-BSD-Lizenz erteilt wurde.

Referenzen

[1]

Robert Bridson, „Fast Poisson Disk Sampling in Arbitrary Dimensions.“ SIGGRAPH, 2007.

Beispiele

Erzeugt eine 2D-Stichprobe mit einem radius von 0,2.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from matplotlib.collections import PatchCollection
>>> from scipy.stats import qmc
>>>
>>> rng = np.random.default_rng()
>>> radius = 0.2
>>> engine = qmc.PoissonDisk(d=2, radius=radius, rng=rng)
>>> sample = engine.random(20)

Visualisiert die 2D-Stichprobe und zeigt, dass keine Punkte näher als der radius sind. radius/2 wird verwendet, um sich nicht überschneidende Kreise zu visualisieren. Wenn zwei Stichproben genau den Abstand radius voneinander haben, berühren sich ihre Kreise mit Radius radius/2.

>>> fig, ax = plt.subplots()
>>> _ = ax.scatter(sample[:, 0], sample[:, 1])
>>> circles = [plt.Circle((xi, yi), radius=radius/2, fill=False)
...            for xi, yi in sample]
>>> collection = PatchCollection(circles, match_original=True)
>>> ax.add_collection(collection)
>>> _ = ax.set(aspect='equal', xlabel=r'$x_1$', ylabel=r'$x_2$',
...            xlim=[0, 1], ylim=[0, 1])
>>> plt.show()
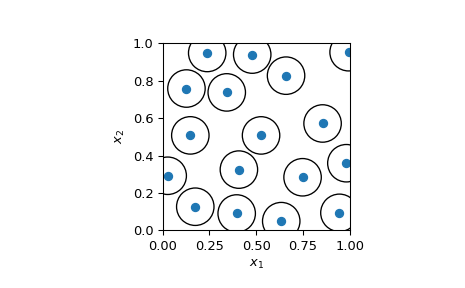
../../_images/scipy-stats-qmc-PoissonDisk-1_00_00.png

Eine solche Visualisierung kann als Kreispackung betrachtet werden: Wie viele Kreise können wir im Raum unterbringen? Dies ist ein NP-schweres Problem. Die Methode fill_space kann verwendet werden, um Stichproben hinzuzufügen, bis keine weiteren Stichproben hinzugefügt werden können. Dies ist ein schwieriges Problem und die Parameter müssen möglicherweise manuell angepasst werden. Achten Sie auf die Dimension: Mit zunehmender Dimensionalität steigt die Anzahl der benötigten Stichproben, um den Raum zu füllen, exponentiell an (Fluch der Dimensionalität).

Auf dieser Seite