scipy.stats.

yeojohnson_llf#

scipy.stats.yeojohnson_llf(lmb, data)[Quelle]#

Die Yeo-Johnson Log-Likelihood-Funktion.

Parameter:

lmbSkalar: Parameter für die Yeo-Johnson-Transformation. Details siehe yeojohnson.
dataarray_like: Daten, für die die Yeo-Johnson Log-Likelihood berechnet werden soll. Wenn data mehrdimensional ist, wird die Log-Likelihood entlang der ersten Achse berechnet.

Rückgabe:

llffloat: Yeo-Johnson Log-Likelihood von data gegeben lmb.

Siehe auch

yeojohnson, probplot, yeojohnson_normplot, yeojohnson_normmax

Hinweise

Die Yeo-Johnson Log-Likelihood-Funktion \(l\) ist hier definiert als

\[l = -\frac{N}{2} \log(\hat{\sigma}^2) + (\lambda - 1) \sum_i^N \text{sign}(x_i) \log(|x_i| + 1)\]

wobei \(N\) die Anzahl der Datenpunkte \(x`=``data`\) ist und \(\hat{\sigma}^2\) die geschätzte Varianz der Yeo-Johnson-transformierten Eingabedaten \(x\) ist. Dies entspricht der *Profil-Log-Likelihood* der ursprünglichen Daten \(x\), wobei einige konstante Terme weggelassen wurden.

Hinzugefügt in Version 1.2.0.

Beispiele

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.axes_grid1.inset_locator import inset_axes

Einige Zufallsvariaten generieren und Yeo-Johnson Log-Likelihood-Werte für diese für einen Bereich von lmbda-Werten berechnen.

>>> x = stats.loggamma.rvs(5, loc=10, size=1000)
>>> lmbdas = np.linspace(-2, 10)
>>> llf = np.zeros(lmbdas.shape, dtype=float)
>>> for ii, lmbda in enumerate(lmbdas):
...     llf[ii] = stats.yeojohnson_llf(lmbda, x)

Auch den optimalen lmbda-Wert mit yeojohnson finden.

>>> x_most_normal, lmbda_optimal = stats.yeojohnson(x)

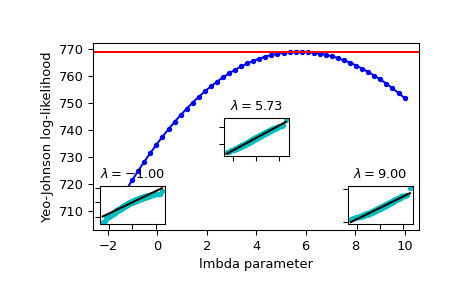
Die Log-Likelihood als Funktion von lmbda plotten. Die optimale lmbda als horizontale Linie hinzufügen, um zu überprüfen, ob dies wirklich das Optimum ist.

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(lmbdas, llf, 'b.-')
>>> ax.axhline(stats.yeojohnson_llf(lmbda_optimal, x), color='r')
>>> ax.set_xlabel('lmbda parameter')
>>> ax.set_ylabel('Yeo-Johnson log-likelihood')

Nun einige Wahrscheinlichkeitsdiagramme hinzufügen, um zu zeigen, dass dort, wo die Log-Likelihood maximiert wird, die mit yeojohnson transformierten Daten am ehesten normal aussehen.

>>> locs = [3, 10, 4]  # 'lower left', 'center', 'lower right'
>>> for lmbda, loc in zip([-1, lmbda_optimal, 9], locs):
...     xt = stats.yeojohnson(x, lmbda=lmbda)
...     (osm, osr), (slope, intercept, r_sq) = stats.probplot(xt)
...     ax_inset = inset_axes(ax, width="20%", height="20%", loc=loc)
...     ax_inset.plot(osm, osr, 'c.', osm, slope*osm + intercept, 'k-')
...     ax_inset.set_xticklabels([])
...     ax_inset.set_yticklabels([])
...     ax_inset.set_title(r'$\lambda=%1.2f$' % lmbda)

>>> plt.show()

../../_images/scipy-stats-yeojohnson_llf-1.png