Einfache Verhältnis-der-Gleichverteilungen (SROU)#
Erforderlich: PDF, Fläche unter der PDF, falls anders als 1
Optional: Modus, CDF am Modus
Geschwindigkeit
Einrichtung: schnell
Stichprobenerstellung: langsam
SROU basiert auf der Methode des Verhältnisses der Gleichverteilungen, die universelle Ungleichungen zur Konstruktion eines (universellen) begrenzenden Rechtecks verwendet. Sie funktioniert für T-konkave Verteilungen mit T(x) = -1/sqrt(x).
>>> import numpy as np
>>> from scipy.stats.sampling import SimpleRatioUniforms
Angenommen, wir haben die Normalverteilung
>>> class StdNorm:
... def pdf(self, x):
... return np.exp(-0.5 * x**2)
Beachten Sie, dass die PDF nicht zu 1 integriert. Wir können entweder die exakte Fläche unter der PDF während der Initialisierung des Generators übergeben oder eine Obergrenze für die exakte Fläche unter der PDF. Außerdem wird empfohlen, den Modus der Verteilung zu übergeben, um die Einrichtung zu beschleunigen.
>>> urng = np.random.default_rng()
>>> dist = StdNorm()
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... random_state=urng)
Nun können wir die Methode rvs verwenden, um Stichproben aus der Verteilung zu generieren
>>> rvs = rng.rvs(10)
Wenn die CDF am Modus verfügbar ist, kann sie gesetzt werden, um die Leistung von rvs zu verbessern.
>>> from scipy.stats import norm
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... cdf_at_mode=norm.cdf(0),
... random_state=urng)
>>> rvs = rng.rvs(1000)
Wir können überprüfen, ob die Stichproben aus der gegebenen Verteilung stammen, indem wir ihr Histogramm visualisieren.
>>> from scipy.stats.sampling import SimpleRatioUniforms
>>> from scipy.stats import norm
>>> import matplotlib.pyplot as plt
>>> class StdNorm:
... def pdf(self, x):
... return np.exp(-0.5 * x**2)
...
>>> urng = np.random.default_rng()
>>> dist = StdNorm()
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... cdf_at_mode=norm.cdf(0),
... random_state=urng)
>>> rvs = rng.rvs(1000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = 1/np.sqrt(2*np.pi) * dist.pdf(x)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> ax.hist(rvs, bins=10, density=True, alpha=0.8, label='random variates')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PDF(x)')
>>> ax.set_title('Simple Ratio-of-Uniforms Samples')
>>> ax.legend()
>>> plt.show()
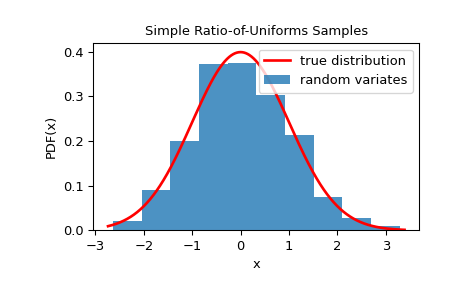
Der Hauptvorteil der Methode ist eine schnelle Einrichtung. Dies kann von Vorteil sein, wenn man wiederholt kleine bis moderate Stichproben einer Verteilung mit unterschiedlichen Formparametern generieren muss. In einer solchen Situation führt die Einrichtungsphase von sampling.NumericalInverseHermite oder sampling.NumericalInversePolynomial zu schlechter Leistung. Als Beispiel nehmen wir an, dass wir 100 Stichproben für die Gamma-Verteilung mit 1000 verschiedenen Formparametern generieren möchten, die durch np.arange(1.5, 5, 1000) gegeben sind.
>>> import math
>>> class GammaDist:
... def __init__(self, p):
... self.p = p
... def pdf(self, x):
... return x**(self.p-1) * np.exp(-x)
...
>>> urng = np.random.default_rng()
>>> p = np.arange(1.5, 5, 1000)
>>> res = np.empty((1000, 100))
>>> for i in range(1000):
... dist = GammaDist(p[i])
... rng = SimpleRatioUniforms(dist, mode=p[i]-1,
... pdf_area=math.gamma(p[i]),
... random_state=urng)
... with np.testing.suppress_warnings() as sup:
... sup.filter(RuntimeWarning, "invalid value encountered in double_scalars")
... sup.filter(RuntimeWarning, "overflow encountered in exp")
... res[i] = rng.rvs(100)
Weitere Details finden Sie unter [1], [2] und [3].