Signalverarbeitung (scipy.signal)

Die Signalverarbeitungsbibliothek enthält derzeit einige Filterfunktionen, eine begrenzte Auswahl an Werkzeugen zur Filterentwurfsverfahren sowie einige B-Spline-Interpolationsalgorithmen für 1- und 2-D-Daten. Obwohl die B-Spline-Algorithmen technisch gesehen unter die Interpolationskategorie fallen könnten, sind sie hier enthalten, da sie nur mit gleichmäßig verteilten Daten funktionieren und stark auf Filtertheorie und Übertragungsfunktionsformulierungen zurückgreifen, um eine schnelle B-Spline-Transformation bereitzustellen. Um diesen Abschnitt zu verstehen, müssen Sie wissen, dass ein Signal in SciPy ein Array von reellen oder komplexen Zahlen ist.

B-Splines

Ein B-Spline ist eine Approximation einer kontinuierlichen Funktion über einem endlichen Bereich in Form von B-Spline-Koeffizienten und Knotenpunkten. Wenn die Knotenpunkte gleichmäßig mit dem Abstand \(\Delta x\) beabstandet sind, dann ist die B-Spline-Approximation einer 1-D-Funktion die Finite-Basis-Expansion.

\[y\left(x\right)\approx\sum_{j}c_{j}\beta^{o}\left(\frac{x}{\Delta x}-j\right).\]

In zwei Dimensionen mit Knotenabstand \(\Delta x\) und \(\Delta y\) ist die Funktionsdarstellung

\[z\left(x,y\right)\approx\sum_{j}\sum_{k}c_{jk}\beta^{o}\left(\frac{x}{\Delta x}-j\right)\beta^{o}\left(\frac{y}{\Delta y}-k\right).\]

In diesen Ausdrücken ist \(\beta^{o}\left(\cdot\right)\) die raumlimitierte B-Spline-Basisfunktion der Ordnung \(o\). Die Anforderung von gleichmäßig beabstandeten Knotenpunkten und gleichmäßig beabstandeten Datenpunkten ermöglicht die Entwicklung schneller (Inverse-Filter-)Algorithmen zur Bestimmung der Koeffizienten, \(c_{j}\), aus Stichprobenwerten, \(y_{n}\). Im Gegensatz zu allgemeinen Spline-Interpolationsalgorithmen können diese Algorithmen schnell die Spline-Koeffizienten für große Bilder finden.

Der Vorteil der Darstellung einer Menge von Stichproben durch B-Spline-Basisfunktionen besteht darin, dass kontinuierliche Operatoren (Ableitungen, Neusamplung, Integral usw.), die davon ausgehen, dass die Datenstichproben aus einer zugrunde liegenden kontinuierlichen Funktion stammen, mit relativer Leichtigkeit aus den Spline-Koeffizienten berechnet werden können. Zum Beispiel ist die zweite Ableitung eines Splines

\[y{}^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\beta^{o\prime\prime}\left(\frac{x}{\Delta x}-j\right).\]

Unter Verwendung der Eigenschaft von B-Splines, dass

\[\frac{d^{2}\beta^{o}\left(w\right)}{dw^{2}}=\beta^{o-2}\left(w+1\right)-2\beta^{o-2}\left(w\right)+\beta^{o-2}\left(w-1\right),\]

kann man sehen, dass

\[y^{\prime\prime}\left(x\right)=\frac{1}{\Delta x^{2}}\sum_{j}c_{j}\left[\beta^{o-2}\left(\frac{x}{\Delta x}-j+1\right)-2\beta^{o-2}\left(\frac{x}{\Delta x}-j\right)+\beta^{o-2}\left(\frac{x}{\Delta x}-j-1\right)\right].\]

Wenn \(o=3\), dann an den Stichprobenpunkten

\begin{eqnarray*} \Delta x^{2}\left.y^{\prime}\left(x\right)\right|_{x=n\Delta x} & = & \sum_{j}c_{j}\delta_{n-j+1}-2c_{j}\delta_{n-j}+c_{j}\delta_{n-j-1},\\ & = & c_{n+1}-2c_{n}+c_{n-1}.\end{eqnarray*}

Somit kann das Signal der zweiten Ableitung leicht aus dem Spline-Fit berechnet werden. Bei Bedarf können Glättungs-Splines gefunden werden, um die zweite Ableitung weniger empfindlich auf zufällige Fehler reagieren zu lassen.

Der aufmerksame Leser wird bereits bemerkt haben, dass die Datenstichproben über einen Faltungsoperator mit den Knotenkoeffizienten zusammenhängen, so dass eine einfache Faltung mit der Abtast-B-Spline-Funktion die Originaldaten aus den Spline-Koeffizienten wiedergewinnt. Die Ausgabe von Faltungen kann je nach Handhabung der Grenzen variieren (dies wird mit zunehmender Dimensionalität des Datensatzes immer wichtiger). Die Algorithmen im Zusammenhang mit B-Splines im Unterpaket für Signalverarbeitung gehen von spiegelbildlich-symmetrischen Randbedingungen aus. Daher werden Spline-Koeffizienten basierend auf dieser Annahme berechnet, und Datenstichproben können aus den Spline-Koeffizienten exakt wiederhergestellt werden, indem ebenfalls von spiegelbildlich-symmetrischen ausgegangen wird.

Derzeit bietet das Paket Funktionen zur Bestimmung von B-Spline-Koeffizienten zweiter und dritter Ordnung aus gleichmäßig beabstandeten Stichproben in einer und zwei Dimensionen (qspline1d, qspline2d, cspline1d, cspline2d). Für große \(o\) kann die B-Spline-Basisfunktion gut durch eine Gaußsche Funktion mit Mittelwert Null und Standardabweichung \(\sigma_{o}=\left(o+1\right)/12\) angenähert werden.

\[\beta^{o}\left(x\right)\approx\frac{1}{\sqrt{2\pi\sigma_{o}^{2}}}\exp\left(-\frac{x^{2}}{2\sigma_{o}}\right).\]

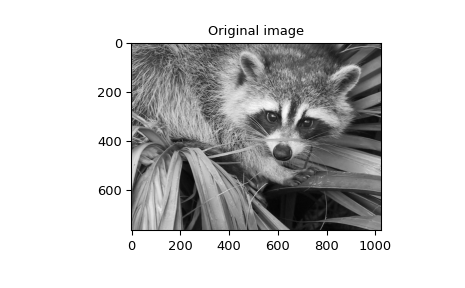
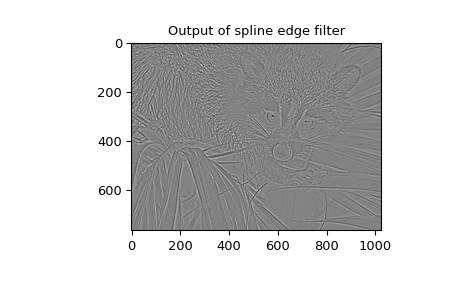
Eine Funktion zur Berechnung dieses Gauß-Wertes für beliebige \(x\) und \(o\) ist ebenfalls verfügbar (gauss_spline). Der folgende Code und die Abbildung verwenden Spline-Filterung zur Berechnung eines Kantenbildes (der zweiten Ableitung eines geglätteten Splines) aus dem Gesicht eines Waschbären, das ein Array ist, das vom Befehl scipy.datasets.face zurückgegeben wird. Der Befehl sepfir2d wurde verwendet, um einen separablen 2-D-FIR-Filter mit spiegelbildlich-symmetrischen Randbedingungen auf die Spline-Koeffizienten anzuwenden. Diese Funktion ist ideal geeignet, um Stichproben aus Spline-Koeffizienten zu rekonstruieren und ist schneller als convolve2d, welche beliebige 2-D-Filter faltet und die Auswahl spiegelbildlich-symmetrischer Randbedingungen ermöglicht.

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = datasets.face(gray=True).astype(np.float32)
>>> derfilt = np.array([1.0, -2, 1.0], dtype=np.float32)
>>> ck = signal.cspline2d(image, 8.0)
>>> deriv = (signal.sepfir2d(ck, derfilt, [1]) +
...          signal.sepfir2d(ck, [1], derfilt))

Alternativ hätten wir folgendes tun können

laplacian = np.array([[0,1,0], [1,-4,1], [0,1,0]], dtype=np.float32)
deriv2 = signal.convolve2d(ck,laplacian,mode='same',boundary='symm')

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(deriv)
>>> plt.gray()
>>> plt.title('Output of spline edge filter')
>>> plt.show()

Filterung

Filterung ist ein allgemeiner Name für jedes System, das ein Eingangssignal auf irgendeine Weise modifiziert. In SciPy kann ein Signal als NumPy-Array betrachtet werden. Es gibt verschiedene Arten von Filtern für unterschiedliche Arten von Operationen. Es gibt zwei breite Arten von Filteroperationen: linear und nicht-linear. Lineare Filter können immer auf die Multiplikation des abgeflachten NumPy-Arrays mit einer geeigneten Matrix reduziert werden, was zu einem anderen abgeflachten NumPy-Array führt. Dies ist natürlich nicht die beste Methode zur Berechnung des Filters, da die beteiligten Matrizen und Vektoren riesig sein können. Zum Beispiel würde das Filtern eines \(512 \times 512\) Bildes mit dieser Methode die Multiplikation einer \(512^2 \times 512^2\) Matrix mit einem \(512^2\) Vektor erfordern. Allein der Versuch, die \(512^2 \times 512^2\) Matrix mit einem Standard-NumPy-Array zu speichern, würde \(68.719.476.736\) Elemente erfordern. Bei 4 Bytes pro Element wären dies \(256\textrm{GB}\) Speicher. In den meisten Anwendungen sind die meisten Elemente dieser Matrix Null und eine andere Methode zur Berechnung der Filterausgabe wird verwendet.

Faltung/Korrelation

Viele lineare Filter haben auch die Eigenschaft der Verschiebungsunabhängigkeit. Das bedeutet, dass die Filteroperation an verschiedenen Stellen im Signal gleich ist und impliziert, dass die Filtermatrix aus der Kenntnis einer Zeile (oder Spalte) der Matrix allein aufgebaut werden kann. In diesem Fall kann die Matrixmultiplikation unter Verwendung von Fourier-Transformationen durchgeführt werden.

Sei \(x\left[n\right]\) ein 1-D-Signal, das durch die ganze Zahl \(n\) indiziert ist. Die volle Faltung zweier 1-D-Signale kann ausgedrückt werden als

\[y\left[n\right]=\sum_{k=-\infty}^{\infty}x\left[k\right]h\left[n-k\right].\]

Diese Gleichung kann nur direkt implementiert werden, wenn wir die Sequenzen auf endlich unterstützte Sequenzen beschränken, die in einem Computer gespeichert werden können. Wählen Sie \(n=0\) als Startpunkt beider Sequenzen, sei \(K+1\) der Wert, für den \(x\left[n\right]=0\) für alle \(n\geq K+1\) und \(M+1\) der Wert, für den \(h\left[n\right]=0\) für alle \(n\geq M+1\) gilt, dann ist der diskrete Faltungsausdruck

\[y\left[n\right]=\sum_{k=\max\left(n-M,0\right)}^{\min\left(n,K\right)}x\left[k\right]h\left[n-k\right].\]

Nehmen wir zur Vereinfachung an, dass \(K\geq M.\) Dann ist expliziter die Ausgabe dieser Operation

\begin{eqnarray*} y\left[0\right] & = & x\left[0\right]h\left[0\right]\\ y\left[1\right] & = & x\left[0\right]h\left[1\right]+x\left[1\right]h\left[0\right]\\ y\left[2\right] & = & x\left[0\right]h\left[2\right]+x\left[1\right]h\left[1\right]+x\left[2\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[M\right] & = & x\left[0\right]h\left[M\right]+x\left[1\right]h\left[M-1\right]+\cdots+x\left[M\right]h\left[0\right]\\ y\left[M+1\right] & = & x\left[1\right]h\left[M\right]+x\left[2\right]h\left[M-1\right]+\cdots+x\left[M+1\right]h\left[0\right]\\ \vdots & \vdots & \vdots\\ y\left[K\right] & = & x\left[K-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[0\right]\\ y\left[K+1\right] & = & x\left[K+1-M\right]h\left[M\right]+\cdots+x\left[K\right]h\left[1\right]\\ \vdots & \vdots & \vdots\\ y\left[K+M-1\right] & = & x\left[K-1\right]h\left[M\right]+x\left[K\right]h\left[M-1\right]\\ y\left[K+M\right] & = & x\left[K\right]h\left[M\right].\end{eqnarray*}

Somit ergibt die vollständige diskrete Faltung zweier endlicher Sequenzen der Längen \(K+1\) bzw. \(M+1\) eine endliche Sequenz der Länge \(K+M+1=\left(K+1\right)+\left(M+1\right)-1.\)

1-D-Faltung wird in SciPy mit der Funktion convolve implementiert. Diese Funktion nimmt die Signale \(x,\) \(h\) und zwei optionale Flags ‘mode’ und ‘method’ als Eingabe und gibt das Signal \(y\) zurück.

Das erste optionale Flag, ‘mode’, erlaubt die Angabe, welcher Teil des Ausgabesignals zurückgegeben werden soll. Der Standardwert ‘full’ gibt das gesamte Signal zurück. Wenn das Flag den Wert ‘same’ hat, werden nur die mittleren \(K\) Werte zurückgegeben, beginnend bei \(y\left[\left\lfloor \frac{M-1}{2}\right\rfloor \right]\), so dass die Ausgabe die gleiche Länge wie die erste Eingabe hat. Wenn das Flag den Wert ‘valid’ hat, werden nur die mittleren \(K-M+1=\left(K+1\right)-\left(M+1\right)+1\) Ausgabewerte zurückgegeben, wobei \(z\) von allen Werten des kleinsten Eingangs von \(h\left[0\right]\) bis \(h\left[M\right]\) abhängt. Mit anderen Worten, es werden nur die Werte \(y\left[M\right]\) bis \(y\left[K\right]\) einschließlich zurückgegeben.

Das zweite optionale Flag, ‘method’, bestimmt, wie die Faltung berechnet wird, entweder über den Fourier-Transformationsansatz mit fftconvolve oder über die direkte Methode. Standardmäßig wählt es die voraussichtlich schnellere Methode. Die Fourier-Transformationsmethode hat die Ordnung \(O(N\log N)\), während die direkte Methode die Ordnung \(O(N^2)\) hat. Abhängig von der Konstante des großen O und dem Wert von \(N\) kann eine dieser beiden Methoden schneller sein. Der Standardwert ‘auto’ führt eine grobe Berechnung durch und wählt die voraussichtlich schnellere Methode, während die Werte ‘direct’ und ‘fft’ die Berechnung mit den beiden anderen Methoden erzwingen.

Der folgende Code zeigt ein einfaches Beispiel für die Faltung von 2 Sequenzen

>>> x = np.array([1.0, 2.0, 3.0])
>>> h = np.array([0.0, 1.0, 0.0, 0.0, 0.0])
>>> signal.convolve(x, h)
array([ 0.,  1.,  2.,  3.,  0.,  0.,  0.])
>>> signal.convolve(x, h, 'same')
array([ 2.,  3.,  0.])

Diese gleiche Funktion convolve kann tatsächlich N-D-Arrays als Eingaben annehmen und gibt die N-D-Faltung der beiden Arrays zurück, wie im folgenden Codebeispiel gezeigt. Die gleichen Eingabeflags sind auch für diesen Fall verfügbar.

>>> x = np.array([[1., 1., 0., 0.], [1., 1., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]])
>>> h = np.array([[1., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 1., 0.], [0., 0., 0., 0.]])
>>> signal.convolve(x, h)
array([[ 1.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 1.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.]])

Korrelation ist sehr ähnlich wie Faltung, außer dass das Minuszeichen zu einem Pluszeichen wird. Somit

\[w\left[n\right]=\sum_{k=-\infty}^{\infty}y\left[k\right]x\left[n+k\right],\]

ist die (Kreuz-)Korrelation der Signale \(y\) und \(x.\) Für endlich lange Signale mit \(y\left[n\right]=0\) außerhalb des Bereichs \(\left[0,K\right]\) und \(x\left[n\right]=0\) außerhalb des Bereichs \(\left[0,M\right],\) kann die Summe vereinfacht werden zu

\[w\left[n\right]=\sum_{k=\max\left(0,-n\right)}^{\min\left(K,M-n\right)}y\left[k\right]x\left[n+k\right].\]

Unter der Annahme, dass \(K\geq M\), ist dies

\begin{eqnarray*} w\left[-K\right] & = & y\left[K\right]x\left[0\right]\\ w\left[-K+1\right] & = & y\left[K-1\right]x\left[0\right]+y\left[K\right]x\left[1\right]\\ \vdots & \vdots & \vdots\\ w\left[M-K\right] & = & y\left[K-M\right]x\left[0\right]+y\left[K-M+1\right]x\left[1\right]+\cdots+y\left[K\right]x\left[M\right]\\ w\left[M-K+1\right] & = & y\left[K-M-1\right]x\left[0\right]+\cdots+y\left[K-1\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[-1\right] & = & y\left[1\right]x\left[0\right]+y\left[2\right]x\left[1\right]+\cdots+y\left[M+1\right]x\left[M\right]\\ w\left[0\right] & = & y\left[0\right]x\left[0\right]+y\left[1\right]x\left[1\right]+\cdots+y\left[M\right]x\left[M\right]\\ w\left[1\right] & = & y\left[0\right]x\left[1\right]+y\left[1\right]x\left[2\right]+\cdots+y\left[M-1\right]x\left[M\right]\\ w\left[2\right] & = & y\left[0\right]x\left[2\right]+y\left[1\right]x\left[3\right]+\cdots+y\left[M-2\right]x\left[M\right]\\ \vdots & \vdots & \vdots\\ w\left[M-1\right] & = & y\left[0\right]x\left[M-1\right]+y\left[1\right]x\left[M\right]\\ w\left[M\right] & = & y\left[0\right]x\left[M\right].\end{eqnarray*}

Die SciPy-Funktion correlate implementiert diese Operation. Äquivalente Flags sind für diese Operation verfügbar, um die vollständige Sequenz der Länge \(K+M+1\) (‘full’) oder eine Sequenz mit der gleichen Größe wie die größte Sequenz, beginnend bei \(w\left[-K+\left\lfloor \frac{M-1}{2}\right\rfloor \right]\) (‘same’), oder eine Sequenz, bei der die Werte von allen Werten der kleinsten Sequenz abhängen (‘valid’), zurückzugeben. Diese letzte Option gibt die \(K-M+1\) Werte \(w\left[M-K\right]\) bis \(w\left[0\right]\) einschließlich zurück.

Die Funktion correlate kann auch beliebige N-D-Arrays als Eingabe annehmen und die N-D-Faltung der beiden Arrays als Ausgabe zurückgeben.

Wenn \(N=2,\) können correlate und/oder convolve verwendet werden, um beliebige Bildfilter zu konstruieren, um Aktionen wie Weichzeichnen, Verbessern und Kantenerkennung für ein Bild durchzuführen.

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = datasets.face(gray=True)
>>> w = np.zeros((50, 50))
>>> w[0][0] = 1.0
>>> w[49][25] = 1.0
>>> image_new = signal.fftconvolve(image, w)

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(image_new)
>>> plt.gray()
>>> plt.title('Filtered image')
>>> plt.show()

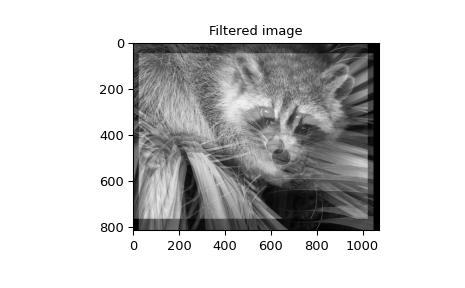
Die Berechnung der Faltung im Zeitbereich wie oben wird hauptsächlich zur Filterung verwendet, wenn eines der Signale viel kleiner als das andere ist ( \(K\gg M\) ); andernfalls wird die lineare Filterung im Frequenzbereich effizienter berechnet, der von der Funktion fftconvolve bereitgestellt wird. Standardmäßig schätzt convolve die schnellste Methode mit choose_conv_method.

Wenn die Filterfunktion \(w[n,m]\) faktorisierbar ist gemäß

\[h[n, m] = h_1[n] h_2[m],\]

kann die Faltung mittels der Funktion sepfir2d berechnet werden. Als Beispiel betrachten wir einen Gaußschen Filter gaussian

\[h[n, m] \propto e^{-x^2-y^2} = e^{-x^2} e^{-y^2},\]

der oft zum Weichzeichnen verwendet wird.

>>> import numpy as np
>>> from scipy import signal, datasets
>>> import matplotlib.pyplot as plt

>>> image = np.asarray(datasets.ascent(), np.float64)
>>> w = signal.windows.gaussian(51, 10.0)
>>> image_new = signal.sepfir2d(image, w, w)

>>> plt.figure()
>>> plt.imshow(image)
>>> plt.gray()
>>> plt.title('Original image')
>>> plt.show()

>>> plt.figure()
>>> plt.imshow(image_new)
>>> plt.gray()
>>> plt.title('Filtered image')
>>> plt.show()

Differenzgleichungsfilterung

Eine allgemeine Klasse von linearen 1-D-Filtern (die Faltungsfilter einschließt) sind Filter, die durch die Differenzgleichung beschrieben werden

\[\sum_{k=0}^{N}a_{k}y\left[n-k\right]=\sum_{k=0}^{M}b_{k}x\left[n-k\right],\]

wobei \(x\left[n\right]\) die Eingabesequenz und \(y\left[n\right]\) die Ausgabesequenz ist. Wenn wir anfängliche Ruhe annehmen, so dass \(y\left[n\right]=0\) für \(n<0\), dann kann diese Art von Filter mittels Faltung implementiert werden. Die Faltungsfiltersequenz \(h\left[n\right]\) könnte jedoch unendlich sein, wenn \(a_{k}\neq0\) für \(k\geq1.\) Darüber hinaus erlaubt diese allgemeine Klasse von linearen Filtern, Anfangsbedingungen auf \(y\left[n\right]\) für \(n<0\) zu setzen, was zu einem Filter führt, der nicht durch Faltung ausgedrückt werden kann.

Der Differenzgleichungsfilter kann als rekursives Finden von \(y\left[n\right]\) in Bezug auf seine vorherigen Werte betrachtet werden.

\[a_{0}y\left[n\right]=-a_{1}y\left[n-1\right]-\cdots-a_{N}y\left[n-N\right]+\cdots+b_{0}x\left[n\right]+\cdots+b_{M}x\left[n-M\right].\]

Oft wird \(a_{0}=1\) zur Normalisierung gewählt. Die Implementierung dieses allgemeinen Differenzgleichungsfilters in SciPy ist etwas komplizierter als die vorherige Gleichung vermuten lässt. Sie ist so implementiert, dass nur ein Signal verzögert werden muss. Die tatsächlichen Implementierungsgleichungen sind (mit \(a_{0}=1\) )

\begin{eqnarray*} y\left[n\right] & = & b_{0}x\left[n\right]+z_{0}\left[n-1\right]\\ z_{0}\left[n\right] & = & b_{1}x\left[n\right]+z_{1}\left[n-1\right]-a_{1}y\left[n\right]\\ z_{1}\left[n\right] & = & b_{2}x\left[n\right]+z_{2}\left[n-1\right]-a_{2}y\left[n\right]\\ \vdots & \vdots & \vdots\\ z_{K-2}\left[n\right] & = & b_{K-1}x\left[n\right]+z_{K-1}\left[n-1\right]-a_{K-1}y\left[n\right]\\ z_{K-1}\left[n\right] & = & b_{K}x\left[n\right]-a_{K}y\left[n\right],\end{eqnarray*}

wobei \(K=\max\left(N,M\right).\) Beachten Sie, dass \(b_{K}=0\) wenn \(K>M\) und \(a_{K}=0\) wenn \(K>N.\) Auf diese Weise hängt die Ausgabe zum Zeitpunkt \(n\) nur von der Eingabe zum Zeitpunkt \(n\) und dem Wert von \(z_{0}\) zum vorherigen Zeitpunkt ab. Dies kann immer berechnet werden, solange die \(K\) Werte \(z_{0}\left[n-1\right]\ldots z_{K-1}\left[n-1\right]\) bei jedem Zeitschritt berechnet und gespeichert werden.

Der Differenzgleichungsfilter wird in SciPy mit dem Befehl lfilter aufgerufen. Dieser Befehl nimmt als Eingaben den Vektor \(b,\) den Vektor \(a,\) ein Signal \(x\) und gibt den Vektor \(y\) (die gleiche Länge wie \(x\) ) zurück, der mit der obigen Gleichung berechnet wurde. Wenn \(x\) N-D ist, wird der Filter entlang der angegebenen Achse berechnet. Bei Bedarf können Anfangsbedingungen, die die Werte von \(z_{0}\left[-1\right]\) bis \(z_{K-1}\left[-1\right]\) liefern, angegeben werden, andernfalls wird davon ausgegangen, dass sie alle Null sind. Wenn Anfangsbedingungen angegeben werden, werden auch die Endbedingungen für die Zwischenvariablen zurückgegeben. Diese könnten beispielsweise verwendet werden, um die Berechnung im gleichen Zustand neu zu starten.

Manchmal ist es bequemer, die Anfangsbedingungen in Bezug auf die Signale \(x\left[n\right]\) und \(y\left[n\right]\) auszudrücken. Mit anderen Worten, vielleicht haben Sie die Werte von \(x\left[-M\right]\) bis \(x\left[-1\right]\) und die Werte von \(y\left[-N\right]\) bis \(y\left[-1\right]\) und möchten wissen, welche Werte von \(z_{m}\left[-1\right]\) als Anfangsbedingungen an den Differenzgleichungsfilter übergeben werden sollten. Es ist nicht schwierig zu zeigen, dass für \(0\leq m<K,\)

\[z_{m}\left[n\right]=\sum_{p=0}^{K-m-1}\left(b_{m+p+1}x\left[n-p\right]-a_{m+p+1}y\left[n-p\right]\right).\]

Mit dieser Formel können wir den Anfangsbedingungsvektor \(z_{0}\left[-1\right]\) bis \(z_{K-1}\left[-1\right]\) finden, gegeben die Anfangsbedingungen für \(y\) (und \(x\) ). Der Befehl lfiltic erfüllt diese Funktion.

Als Beispiel betrachten wir das folgende System

\[y[n] = \frac{1}{2} x[n] + \frac{1}{4} x[n-1] + \frac{1}{3} y[n-1]\]

Der Code berechnet das Signal \(y[n]\) für ein gegebenes Signal \(x[n]\); zuerst für Anfangsbedingungen \(y[-1] = 0\) (Standardfall), dann für \(y[-1] = 2\) mittels lfiltic.

>>> import numpy as np
>>> from scipy import signal

>>> x = np.array([1., 0., 0., 0.])
>>> b = np.array([1.0/2, 1.0/4])
>>> a = np.array([1.0, -1.0/3])
>>> signal.lfilter(b, a, x)
array([0.5, 0.41666667, 0.13888889, 0.0462963])
>>> zi = signal.lfiltic(b, a, y=[2.])
>>> signal.lfilter(b, a, x, zi=zi)
(array([ 1.16666667,  0.63888889,  0.21296296,  0.07098765]), array([0.02366]))

Beachten Sie, dass das Ausgabesignal \(y[n]\) die gleiche Länge wie das Eingangssignal \(x[n]\) hat.

Analyse linearer Systeme

Lineare Systeme, die durch eine lineare Differenzgleichung beschrieben werden, können vollständig durch die Koeffizientenvektoren \(a\) und \(b\) wie oben beschrieben werden. Eine alternative Darstellung besteht darin, einen Faktor \(k\), \(N_z\) Nullstellen \(z_k\) und \(N_p\) Pole \(p_k\) anzugeben, um das System anhand seiner Übertragungsfunktion \(H(z)\) zu beschreiben, gemäß

\[H(z) = k \frac{ (z-z_1)(z-z_2)...(z-z_{N_z})}{ (z-p_1)(z-p_2)...(z-p_{N_p})}.\]

Diese alternative Darstellung kann mit der SciPy-Funktion tf2zpk erhalten werden; die Umkehrung wird von zpk2tf bereitgestellt.

Für das obige Beispiel haben wir

>>> b = np.array([1.0/2, 1.0/4])
>>> a = np.array([1.0, -1.0/3])
>>> signal.tf2zpk(b, a)
(array([-0.5]), array([ 0.33333333]), 0.5)

d.h., das System hat eine Nullstelle bei \(z=-1/2\) und einen Pol bei \(z=1/3\).

Die SciPy-Funktion freqz ermöglicht die Berechnung der Frequenzantwort eines Systems, das durch die Koeffizienten \(a_k\) und \(b_k\) beschrieben wird. Siehe die Hilfe der Funktion freqz für ein umfassendes Beispiel.

Filterentwurf

Zeitdiskrete Filter können in Filter mit endlicher Impulsantwort (FIR) und Filter mit unendlicher Impulsantwort (IIR) eingeteilt werden. FIR-Filter können eine lineare Phasenantwort liefern, während IIR-Filter dies nicht können. SciPy bietet Funktionen für den Entwurf beider Filtertypen.

FIR-Filter

Die Funktion firwin entwirft Filter nach der Fensteremethode. Abhängig von den übergebenen Argumenten liefert die Funktion unterschiedliche Filtertypen (z. B. Tiefpass, Bandstopp).

Das folgende Beispiel entwirft jeweils einen Tiefpass- und einen Bandstoppfilter.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b1 = signal.firwin(40, 0.5)
>>> b2 = signal.firwin(41, [0.3, 0.8])
>>> w1, h1 = signal.freqz(b1)
>>> w2, h2 = signal.freqz(b2)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w1, 20*np.log10(np.abs(h1)), 'b')
>>> plt.plot(w2, 20*np.log10(np.abs(h2)), 'r')
>>> plt.ylabel('Amplitude Response (dB)')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

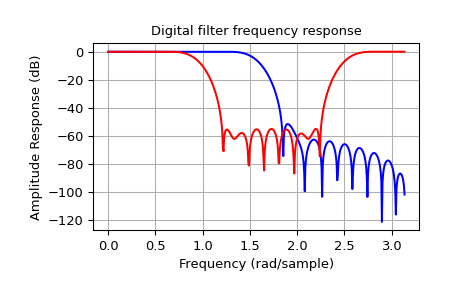
Beachten Sie, dass firwin standardmäßig eine normalisierte Frequenz verwendet, die so definiert ist, dass der Wert \(1\) der Nyquist-Frequenz entspricht, während die Funktion freqz so definiert ist, dass der Wert \(\pi\) der Nyquist-Frequenz entspricht.

Die Funktion firwin2 ermöglicht den Entwurf von nahezu beliebigen Frequenzantworten, indem ein Array von Eckfrequenzen und entsprechenden Verstärkungen angegeben wird.

Das folgende Beispiel entwirft einen Filter mit einer solchen beliebigen Amplitudenantwort.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b = signal.firwin2(150, [0.0, 0.3, 0.6, 1.0], [1.0, 2.0, 0.5, 0.0])
>>> w, h = signal.freqz(b)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w, np.abs(h))
>>> plt.title('Digital filter frequency response')
>>> plt.ylabel('Amplitude Response')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

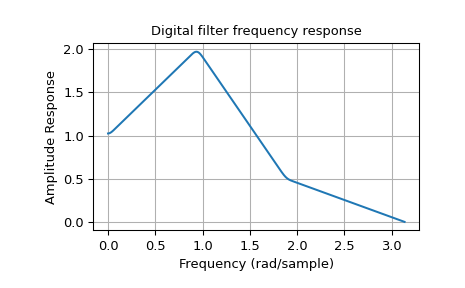
Beachten Sie die lineare Skalierung der y-Achse und die unterschiedliche Definition der Nyquist-Frequenz in firwin2 und freqz (wie oben erläutert).

IIR-Filter

SciPy bietet zwei Funktionen, um IIR-Filter direkt zu entwerfen (iirdesign und iirfilter), wobei der Filtertyp (z. B. elliptisch) als Argument übergeben wird, und mehrere weitere Filterentwurfsfunktionen für spezifische Filtertypen, z. B. ellip.

Das folgende Beispiel entwirft einen elliptischen Tiefpassfilter mit definiertem Bandpass- und Sperrbereichsrippeln. Beachten Sie die viel geringere Filterordnung (Ordnung 4) im Vergleich zu den FIR-Filtern aus den obigen Beispielen, um die gleiche Sperrbereichsdämpfung von \(\approx 60\) dB zu erreichen.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.iirfilter(4, Wn=0.2, rp=5, rs=60, btype='lowpass', ftype='ellip')
>>> w, h = signal.freqz(b, a)

>>> plt.title('Digital filter frequency response')
>>> plt.plot(w, 20*np.log10(np.abs(h)))
>>> plt.title('Digital filter frequency response')
>>> plt.ylabel('Amplitude Response [dB]')
>>> plt.xlabel('Frequency (rad/sample)')
>>> plt.grid()
>>> plt.show()

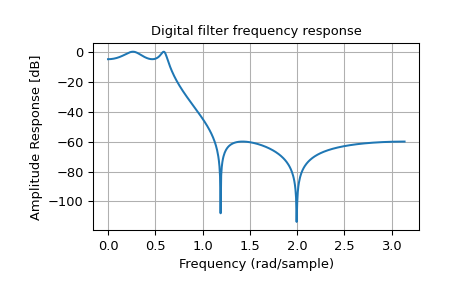
Hinweis

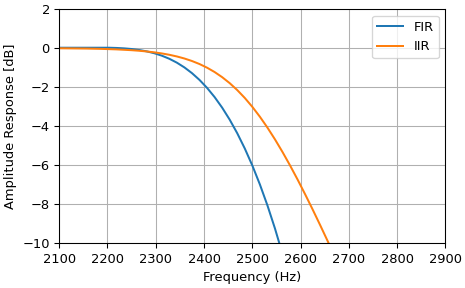
Es ist wichtig zu beachten, dass die Grenzfrequenzen für firwin und iirfilter unterschiedlich definiert sind. Für firwin liegt die Grenzfrequenz bei halber Amplitude (d. h. -6 dB). Für iirfilter liegt die Grenzfrequenz bei halber Leistung (d. h. -3 dB).

>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>> from scipy import signal as sig

>>> fs = 16000
>>> b = sig.firwin(101, 2500, fs=fs)
>>> f, h_fft = sig.freqz(b, fs=fs)
>>> h_amp = 20 * np.log10(np.abs(h_fft))
>>> _, ax = plt.subplots(layout="constrained")
>>> ax.plot(f, h_amp, label="FIR")
>>> ax.grid(True)

>>> b, a = sig.iirfilter(15, 2500, btype="low", fs=fs)
>>> f, h_fft = sig.freqz(b, a, fs=fs)
>>> h_amp = 20 * np.log10(np.abs(h_fft))
>>> ax.plot(f, h_amp, label="IIR")
>>> ax.set(xlim=[2100, 2900], ylim=[-10, 2])
>>> ax.set(xlabel="Frequency (Hz)", ylabel="Amplitude Response [dB]")
>>> ax.legend()

Filterkoeffizienten

Filterkoeffizienten können in verschiedenen Formaten gespeichert werden

• ‘ba’ oder ‘tf’ = Koeffizienten der Übertragungsfunktion

• ‘zpk’ = Nullstellen, Pole und Gesamtgewinn

• ‘ss’ = Zustandsraumdarstellung des Systems

• ‘sos’ = Koeffizienten der Übertragungsfunktion von Zweikreisensektionen

Funktionen wie tf2zpk und zpk2ss können zwischen ihnen konvertieren.

Übertragungsfunktionsdarstellung

Das Format ba oder tf ist ein 2-Tupel (b, a), das eine Übertragungsfunktion darstellt, wobei b ein Array der Länge M+1 mit den Koeffizienten des Zählerpolynoms \(M\)-ten Grades ist und a ein Array der Länge N+1 mit den Koeffizienten des Nennerpolynoms \(N\)-ten Grades ist, und zwar als positive, absteigende Potenzen der Übertragungsfunktionsvariablen. Das Tupel \(b = [b_0, b_1, ..., b_M]\) und \(a =[a_0, a_1, ..., a_N]\) kann somit einen analogen Filter der Form darstellen

\[H(s) = \frac {b_0 s^M + b_1 s^{(M-1)} + \cdots + b_M} {a_0 s^N + a_1 s^{(N-1)} + \cdots + a_N} = \frac {\sum_{i=0}^M b_i s^{(M-i)}} {\sum_{i=0}^N a_i s^{(N-i)}}\]

oder einen zeitdiskreten Filter der Form

\[H(z) = \frac {b_0 z^M + b_1 z^{(M-1)} + \cdots + b_M} {a_0 z^N + a_1 z^{(N-1)} + \cdots + a_N} = \frac {\sum_{i=0}^M b_i z^{(M-i)}} {\sum_{i=0}^N a_i z^{(N-i)}}.\]

Diese Form mit "positiven Potenzen" ist in der Regelungstechnik gebräuchlicher. Wenn M und N gleich sind (was für alle Filter gilt, die durch die Bilinear-Transformation erzeugt werden), dann ist dies äquivalent zur diskreten Zeitform mit "negativen Potenzen", die in der digitalen Signalverarbeitung bevorzugt wird.

\[H(z) = \frac {b_0 + b_1 z^{-1} + \cdots + b_M z^{-M}} {a_0 + a_1 z^{-1} + \cdots + a_N z^{-N}} = \frac {\sum_{i=0}^M b_i z^{-i}} {\sum_{i=0}^N a_i z^{-i}}.\]

Obwohl dies für gängige Filter gilt, denken Sie daran, dass dies im Allgemeinen nicht der Fall ist. Wenn M und N nicht gleich sind, müssen die diskreten Zeitübertragungsfunktionskoeffizienten zuerst in die Form "positive Potenzen" konvertiert werden, bevor die Pole und Nullstellen gefunden werden.

Diese Darstellung leidet unter numerischen Fehlern bei höheren Ordnungen, daher werden andere Formate bevorzugt, wenn möglich.

Nullstellen- und Polstellen-Darstellung

Das zpk-Format ist ein 3-Tupel (z, p, k), wobei z ein Array der Länge M der komplexen Nullstellen der Übertragungsfunktion ist \(z = [z_0, z_1, ..., z_{M-1}]\), p ein Array der Länge N der komplexen Pole der Übertragungsfunktion ist \(p = [p_0, p_1, ..., p_{N-1}]\), und k ein Skalargewinn ist. Diese repräsentieren die digitale Übertragungsfunktion

\[H(z) = k \cdot \frac {(z - z_0) (z - z_1) \cdots (z - z_{(M-1)})} {(z - p_0) (z - p_1) \cdots (z - p_{(N-1)})} = k \frac {\prod_{i=0}^{M-1} (z - z_i)} {\prod_{i=0}^{N-1} (z - p_i)}\]

oder die analoge Übertragungsfunktion

\[H(s) = k \cdot \frac {(s - z_0) (s - z_1) \cdots (s - z_{(M-1)})} {(s - p_0) (s - p_1) \cdots (s - p_{(N-1)})} = k \frac {\prod_{i=0}^{M-1} (s - z_i)} {\prod_{i=0}^{N-1} (s - p_i)}.\]

Obwohl die Wurzelmengen als geordnete NumPy-Arrays gespeichert werden, spielt ihre Reihenfolge keine Rolle: ([-1, -2], [-3, -4], 1) ist derselbe Filter wie ([-2, -1], [-4, -3], 1).

Zustandsraumdarstellung

Das ss-Format ist ein 4-Tupel von Arrays (A, B, C, D), das den Zustandsraum eines digitalen/diskreten Systems der Ordnung N vom Typ darstellt

\[\begin{split}\mathbf{x}[k+1] = A \mathbf{x}[k] + B \mathbf{u}[k]\\ \mathbf{y}[k] = C \mathbf{x}[k] + D \mathbf{u}[k]\end{split}\]

oder eines kontinuierlichen/analogen Systems vom Typ

\[\begin{split}\dot{\mathbf{x}}(t) = A \mathbf{x}(t) + B \mathbf{u}(t)\\ \mathbf{y}(t) = C \mathbf{x}(t) + D \mathbf{u}(t),\end{split}\]

mit P Eingängen, Q Ausgängen und N Zustandsvariablen, wobei

• x der Zustandsvektor ist

• y der Ausgangsvektor der Länge Q ist

• u der Eingangsvektor der Länge P ist

• A die Zustandsmatrix mit der Form (N, N) ist

• B die Eingangsmatrix mit der Form (N, P) ist

• C die Ausgangsmatrix mit der Form (Q, N) ist

• D die Durchgriffs- oder Vorsteuerungsmatrix mit der Form (Q, P) ist. (In Fällen, in denen das System keinen direkten Durchgriff hat, sind alle Werte in D Null.)

Der Zustandsraum ist die allgemeinste Darstellung und die einzige, die Mehrfacheingangs-Mehrfachausgangssysteme (MIMO) zulässt. Für eine gegebene Übertragungsfunktion gibt es mehrere Zustandsraumdarstellungen. Insbesondere die "steuerbare kanonische Form" und die "beobachtbare kanonische Form" haben dieselben Koeffizienten wie die tf-Darstellung und leiden daher unter denselben numerischen Fehlern.

Zweite-Ordnung-Abschnitte-Darstellung

Das sos-Format ist ein einzelnes 2D-Array der Form (n_sections, 6), das eine Folge von Zweite-Ordnung-Übertragungsfunktionen darstellt, die in Serie kaskadiert eine höherstufige Filterung mit minimalen numerischen Fehlern realisieren. Jede Zeile entspricht einer Zweite-Ordnung tf-Darstellung, wobei die ersten drei Spalten die Zählerkoeffizienten und die letzten drei die Nennerkoeffizienten liefern

\[[b_0, b_1, b_2, a_0, a_1, a_2]\]

Die Koeffizienten sind typischerweise normiert, so dass \(a_0\) immer 1 ist. Die Reihenfolge der Abschnitte ist bei Fließkommaberechnungen normalerweise nicht wichtig; die Filter-Ausgabe ist unabhängig von der Reihenfolge gleich.

Filtertransformationen

Die Funktionen zur Auslegung von IIR-Filtern erzeugen zunächst einen prototypischen analogen Tiefpassfilter mit einer normierten Grenzfrequenz von 1 rad/Sekunde. Dieser wird dann durch folgende Substitutionen in andere Frequenzen und Bandtypen transformiert

Typ	Transformation
lp2lp	\(s \rightarrow \frac{s}{\omega_0}\)
lp2hp	\(s \rightarrow \frac{\omega_0}{s}\)
lp2bp	\(s \rightarrow \frac{s^2 + {\omega_0}^2}{s \cdot \mathrm{BW}}\)
lp2bs	\(s \rightarrow \frac{s \cdot \mathrm{BW}}{s^2 + {\omega_0}^2}\)

Hierbei ist \(\omega_0\) die neue Grenzfrequenz oder Mittenfrequenz und \(\mathrm{BW}\) die Bandbreite. Diese erhalten die Symmetrie auf einer logarithmischen Frequenzachse.

Um den transformierten analogen Filter in einen digitalen Filter umzuwandeln, wird die bilinear-Transformation verwendet, die folgende Substitution vornimmt

\[s \rightarrow \frac{2}{T} \frac{z - 1}{z + 1},\]

wobei T die Abtastzeit (der Kehrwert der Abtastfrequenz) ist.

Andere Filter

Das Signalverarbeitungspaket bietet noch viele weitere Filter an.

Medianfilter

Ein Medianfilter wird üblicherweise angewendet, wenn das Rauschen stark nicht-Gaußsch ist oder wenn Kanten erhalten werden sollen. Der Medianfilter sortiert alle Pixelwerte im Bereich um den interessierenden Punkt. Der Stichprobenmedian dieser Nachbarschaftspixelwerte wird als Wert für das Ausgabearray verwendet. Der Stichprobenmedian ist der mittlere Arraywert in einer sortierten Liste von Nachbarschaftswerten. Wenn die Anzahl der Elemente in der Nachbarschaft gerade ist, wird der Durchschnitt der beiden mittleren Werte als Median verwendet. Ein universell einsetzbarer Medianfilter, der auf N-dimensionale Arrays wirkt, ist medfilt. Eine spezialisierte Version, die nur für 2D-Arrays funktioniert, ist als medfilt2d verfügbar.

Ordnungsfilter

Ein Medianfilter ist ein spezifisches Beispiel für eine allgemeinere Klasse von Filtern, die als Ordnungsfilter bezeichnet werden. Zur Berechnung des Ausgangs an einem bestimmten Pixel werden alle Ordnungsfilter die Arraywerte in einem Bereich um dieses Pixel verwenden. Diese Arraywerte werden sortiert und dann wird einer von ihnen als Ausgangswert ausgewählt. Für den Medianfilter wird der Stichprobenmedian der Liste der Arraywerte als Ausgabe verwendet. Ein allgemeiner Ordnungsfilter ermöglicht es dem Benutzer, auszuwählen, welcher der sortierten Werte als Ausgabe verwendet werden soll. So könnte man zum Beispiel den Maximalwert oder den Minimalwert in der Liste auswählen. Der Ordnungsfilter nimmt neben dem Eingabearray und der Bereichsmaske ein zusätzliches Argument entgegen, das angibt, welches der Elemente in der sortierten Liste der benachbarten Arraywerte als Ausgabe verwendet werden soll. Der Befehl zur Durchführung eines Ordnungsfilters ist order_filter.

Wiener-Filter

Der Wiener-Filter ist ein einfacher Deblurring-Filter zur Entrauschung von Bildern. Dies ist nicht der Wiener-Filter, der üblicherweise in Bildrekonstruktionsproblemen beschrieben wird, sondern ein einfacher lokaler Mittelwertfilter. Sei \(x\) das Eingangssignal, dann ist die Ausgabe

\[\begin{split}y=\left\{ \begin{array}{cc} \frac{\sigma^{2}}{\sigma_{x}^{2}}m_{x}+\left(1-\frac{\sigma^{2}}{\sigma_{x}^{2}}\right)x & \sigma_{x}^{2}\geq\sigma^{2},\\ m_{x} & \sigma_{x}^{2}<\sigma^{2},\end{array}\right.\end{split}\]

wobei \(m_{x}\) die lokale Schätzung des Mittelwerts und \(\sigma_{x}^{2}\) die lokale Schätzung der Varianz ist. Das Fenster für diese Schätzungen ist ein optionaler Eingabeparameter (Standard ist \(3\times3\)). Der Parameter \(\sigma^{2}\) ist ein Schwellenwert-Rauschparameter. Wenn \(\sigma\) nicht gegeben ist, wird es als Durchschnitt der lokalen Varianzen geschätzt.

Hilbert-Filter

Die Hilbert-Transformation konstruiert das komplexwertige analytische Signal aus einem reellen Signal. Wenn beispielsweise \(x=\cos\omega n\) ist, dann gibt \(y=\textrm{hilbert}\left(x\right)\) (außer nahe den Rändern) \(y=\exp\left(j\omega n\right)\) zurück. Im Frequenzbereich führt die Hilbert-Transformation

\[Y=X\cdot H,\]

durch, wobei \(H\) für positive Frequenzen \(2\), für negative Frequenzen \(0\) und für Nullfrequenzen \(1\) ist.

Analogfilterdesign

Die Funktionen iirdesign, iirfilter und die Designfunktionen für spezifische Filtertypen (z.B. ellip) haben alle ein Flag analog, das auch das Design von analogen Filtern ermöglicht.

Das folgende Beispiel entwirft einen analogen (IIR-)Filter, ermittelt über tf2zpk die Pole und Nullstellen und plottet sie in der komplexen s-Ebene. Die Nullstellen bei \(\omega \approx 150\) und \(\omega \approx 300\) sind in der Amplitudenantwort deutlich zu erkennen.

>>> import numpy as np
>>> import scipy.signal as signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.iirdesign(wp=100, ws=200, gpass=2.0, gstop=40., analog=True)
>>> w, h = signal.freqs(b, a)

>>> plt.title('Analog filter frequency response')
>>> plt.plot(w, 20*np.log10(np.abs(h)))
>>> plt.ylabel('Amplitude Response [dB]')
>>> plt.xlabel('Frequency')
>>> plt.grid()
>>> plt.show()

>>> z, p, k = signal.tf2zpk(b, a)

>>> plt.plot(np.real(z), np.imag(z), 'ob', markerfacecolor='none')
>>> plt.plot(np.real(p), np.imag(p), 'xr')
>>> plt.legend(['Zeros', 'Poles'], loc=2)

>>> plt.title('Pole / Zero Plot')
>>> plt.xlabel('Real')
>>> plt.ylabel('Imaginary')
>>> plt.grid()
>>> plt.show()

\[% LaTeX Macros to make the LaTeX formulas more readable: \newcommand{\IC}{{\mathbb{C}}} % set of complex numbers \newcommand{\IN}{{\mathbb{N}}} % set of natural numbers \newcommand{\IR}{{\mathbb{R}}} % set of real numbers \newcommand{\IZ}{{\mathbb{Z}}} % set of integers \newcommand{\jj}{{\mathbb{j}}} % imaginary unit \newcommand{\e}{\operatorname{e}} % Euler's number \newcommand{\dd}{\operatorname{d}} % infinitesimal operator \newcommand{\abs}[1]{\left|#1\right|} % absolute value \newcommand{\conj}[1]{\overline{#1}} % complex conjugate \newcommand{\conjT}[1]{\overline{#1^T}} % transposed complex conjugate \newcommand{\inv}[1]{\left(#1\right)^{\!-1}} % inverse % Since the physics package is not loaded, we define the macros ourselves: \newcommand{\vb}[1]{\mathbf{#1}} % vectors and matrices are bold % new macros: \newcommand{\rect}{\operatorname{rect}} % rect or boxcar function \newcommand{\sinc}{\operatorname{sinc}} % sinc(t) := sin(pi*t) / (pi*t)\]

Spektralanalyse

Spektralanalyse bezieht sich auf die Untersuchung der Fourier-Transformation [1] eines Signals. Je nach Kontext existieren verschiedene Bezeichnungen wie Spektrum, Spektraldichte oder Periodogramm für die verschiedenen spektralen Darstellungen der Fourier-Transformation. [2] Dieser Abschnitt illustriert die gebräuchlichsten Darstellungen am Beispiel einer kontinuierlichen Sinuswelle fester Dauer. Anschließend wird die Verwendung der diskreten Fourier-Transformation [3] auf einer abgetasteten Version dieser Sinuswelle diskutiert.

Separate Unterabschnitte sind dem Phasenspektrum, der Schätzung der Leistungsdichtespektraldichte ohne (periodogram) und mit Mittelung (welch) sowie für ungleich beabstandete Signale (lombscargle) gewidmet.

Beachten Sie, dass das Konzept der Fourier-Reihen eng verwandt ist, sich aber in einem entscheidenden Punkt unterscheidet: Fourier-Reihen haben ein Spektrum, das aus diskreten Frequenzharmonischen besteht, während in diesem Abschnitt die Spektren kontinuierlich in der Frequenz sind.

Kontinuierliches Sinussignal

Betrachten Sie ein Sinussignal mit Amplitude \(a\), Frequenz \(f_x\) und Dauer \(\tau\), d.h.

(1)\[x(t) = a \sin(2 \pi f_x t)\, \rect(\frac{t}{\tau}-\frac{1}{2}) = \left(\frac{a}{2\jj} \e^{\jj 2 \pi f_x t} - \frac{a}{2\jj} \e^{-\jj 2 \pi f_x t} \right) \rect(\frac{t}{\tau}-\frac{1}{2})\ .\]

Da die \(\rect(t)\)-Funktion für \(|t|<1/2\) gleich 1 und für \(|t|>1/2\) gleich 0 ist, beschränkt sie \(x(t)\) auf das Intervall \([0, \tau]\). Die Darstellung des Sinus durch komplexe Exponentialfunktionen zeigt seine beiden periodischen Komponenten mit den Frequenzen \(\pm f_x\). Wir nehmen an, dass \(x(t)\) ein Spannungssignal ist, daher hat es die Einheit \(\text{V}\).

In der Signalverarbeitung wird das Integral des absoluten Quadrats \(|x(t)|^2\) zur Definition von Energie und Leistung eines Signals verwendet, d.h.

(2)\[E_x := \int_0^\tau |x(t)|^2 \dd t\ = \frac{1}{2}|a|^2\tau\ , \qquad P_x := \frac{1}{\tau}E_x = \frac{1}{2}|a|^2\ .\]

Die Leistung \(P_x\) kann als Energie \(E_x\) pro Zeiteinheit interpretiert werden. Hinsichtlich der Einheiten ergibt die Integration über \(t\) eine Multiplikation mit Sekunden. Daher hat \(E_x\) die Einheit \(\text{V}^2\text{s}\) und \(P_x\) die Einheit \(\text{V}^2\).

Anwenden der Fourier-Transformation auf \(x(t)\), d.h.

(3)\[X(f) = \int_{\IR} x(t)\, \e^{-2\jj\pi f t}\, \dd t = \frac{a \tau}{2\jj} \Big( \sinc\!\big(\tau (f-f_x)\big) - \sinc\!\big(\tau (f+f_x)\big) \Big)\e^{-\jj\pi\tau f}\ ,\]

ergibt zwei \(\sinc(f) := \sin(\pi f) /(\pi f)\)-Funktionen, die bei \(\pm f_x\) zentriert sind. Die Amplitude (absoluter Wert) \(|X(f)|\) hat zwei Maxima bei \(\pm f_x\) mit dem Wert \(|a|\tau/2\). Man sieht im untenstehenden Diagramm, dass \(X(f)\) nicht um die Hauptkeulen bei \(\pm f_x\) konzentriert ist, sondern Seitenkeulen mit Höhen enthält, die proportional zu \(1/(\tau f)\) abnehmen. Dieses sogenannte "Spektral-Leckage" [4] wird durch die Beschränkung des Sinus auf ein endliches Intervall verursacht. Je kürzer die Signaldauer \(\tau\) ist, desto höher ist die Leckage. Um unabhängig von der Signaldauer zu sein, kann anstelle des Spektrums \(X(f)\) das sogenannte "Amplitudenspektrum" \(X(f)/\tau\) verwendet werden. Sein Wert bei \(f\) entspricht der Amplitude der komplexen Exponentialfunktion \(\exp(\jj2\pi f t)\).

Aufgrund des Parsevalschen Theorems kann die Energie aus ihrer Fourier-Transformation \(X(f)\) berechnet werden durch

(4)\[ E_X := \int_\IR \abs{X(f)}^2 \dd f = E_x\]

ebenfalls. Zum Beispiel kann durch direkte Berechnung gezeigt werden, dass die Energie von \(X(f)\) aus Gl. (4) \(|a|^2\tau/2\) ist. Somit kann die Leistung des Signals in einem Frequenzband \([f_a, f_b]\) bestimmt werden mit

(5)\[P_X^{a,b} = \frac{1}{\tau} \int_{f_a}^{f_b} \abs{X(f)}^2 \dd f\ .\]

Somit kann die Funktion \(|X(f)|^2\) als sogenannte "Energiespektraldichte" und \(S_{xx}(f) := |X(f)|^2 / \tau\) als "Leistungsdichtespektrum" (PSD) von \(x(t)\) definiert werden. Anstelle der PSD wird auch die sogenannte "Amplitudenspektraldichte" \(X(f) / \sqrt{\tau}\) verwendet, die immer noch die Phaseninformation enthält. Ihr Betragsquadrat ist die PSD und damit eng verwandt mit dem Konzept des Effektivwertes (RMS) \(\sqrt{P_x}\) eines Signals.

Zusammenfassend präsentierte dieser Unterabschnitt fünf Möglichkeiten, ein Spektrum darzustellen

Vergleich von Spektraldarstellungen des Sinussignals \(x(t)\) aus Gl. (1) mit Einheit \(\text{V}\):

	Spektrum	Amplitudenspektrum	Energiespektraldichte	Leistungsdichtespektrum (PSD)	Amplitudenspektraldichte
Definition	\(X(f)\)	\(X(f) / \tau\)	\(|X(f)|^2\)	\(|X(f)|^2 / \tau\)	\(X(f) / \sqrt{\tau}\)
Amplitude bei \(\pm f_x\)	\(\frac{1}{2}|a|\tau\)	\(\frac{1}{2}|a|\)	\(\frac{1}{4}|a|^2\tau^2\)	\(\frac{1}{4}|a|^2\tau\)	\(\frac{1}{2}|a|\sqrt{\tau}\)
Einheit	\(\text{V} / \text{Hz}\)	\(\text{V}\)	\(\text{V}^2\text{s} / \text{Hz}\)	\(\text{V}^2 / \text{Hz}\)	\(\text{V} / \sqrt{\text{Hz}}\)

Beachten Sie, dass die in der obigen Tabelle angegebenen Einheiten nicht eindeutig sind, z.B. \(\text{V}^2\text{s} / \text{Hz} = \text{V}^2\text{s}^2 = \text{V}^2/ \text{Hz}^2\). Wenn der Absolutwert von \(|X(f) / \tau|\) des Amplitudenspektrums verwendet wird, spricht man von einem Betragsspektrum. Darüber hinaus gibt es kein kanonisches Namensschema für die Darstellungen, das in der Literatur einheitlich ist.

Für reellwertige Signale wird oft die sogenannte "einseitige" Spektraldarstellung verwendet. Sie verwendet nur die nicht-negativen Frequenzen (da \(X(-f)= \conj{X}(f)\) wenn \(x(t)\in\IR\)). Manchmal werden die Werte der negativen Frequenzen zu ihren positiven Gegenstücken addiert. Dann erlaubt das Amplitudenspektrum, die volle (nicht halbe) Amplitude des Sinus von \(x(t)\) bei \(f_x\) abzulesen und die Fläche eines Intervalls in der PSD repräsentiert seine volle (nicht halbe) Leistung. Beachten Sie, dass für Amplitudenspektraldichten die positiven Werte nicht verdoppelt, sondern mit \(\sqrt{2}\) multipliziert werden, da sie die Quadratwurzel der PSD sind. Außerdem gibt es keine kanonische Methode, ein verdoppeltes Spektrum zu benennen.

Das folgende Diagramm zeigt drei verschiedene Spektraldarstellungen von vier Sinussignalen \(x(t)\) aus Gl. (1) mit unterschiedlichen Amplituden \(a\) und Dauern \(\tau\). Zur besseren Übersichtlichkeit sind die Spektren bei \(f_x\) zentriert und nebeneinander dargestellt

import matplotlib.pyplot as plt
import numpy as np

aa = [1, 1, 2, 2]  # amplitudes
taus = [1, 2, 1, 2]  # durations

fg0, axx = plt.subplots(3, 1, sharex='all', tight_layout=True, figsize=(6., 4.))
axx[0].set(title=r"Spectrum $|X(f)|$", ylabel="V/Hz")
axx[1].set(title=r"Magnitude Spectrum $|X(f)/\tau|$ ", ylabel=r"V")
axx[2].set(title=r"Amplitude Spectral Density $|X(f)/\sqrt{\tau}|$",
           ylabel=r"$\operatorname{V} / \sqrt{\operatorname{Hz}}$",
           xlabel="Frequency $f$ in Hertz",)

x_labels, x_ticks = [], []
f = np.linspace(-2.5, 2.5, 400)
for c_, (a_, tau_) in enumerate(zip(aa, taus), start=1):
    aZ_, f_ = abs(a_ * tau_ * np.sinc(tau_ * f) / 2), f + c_ * 5
    axx[0].plot(f_, aZ_)
    axx[1].plot(f_, aZ_ / tau_)
    axx[2].plot(f_, aZ_ / np.sqrt(tau_))
    x_labels.append(rf"$a={a_:g}$, $\tau={tau_:g}$")
    x_ticks.append(c_ * 5)

axx[2].set_xticks(x_ticks)
axx[2].set_xticklabels(x_labels)
plt.show()

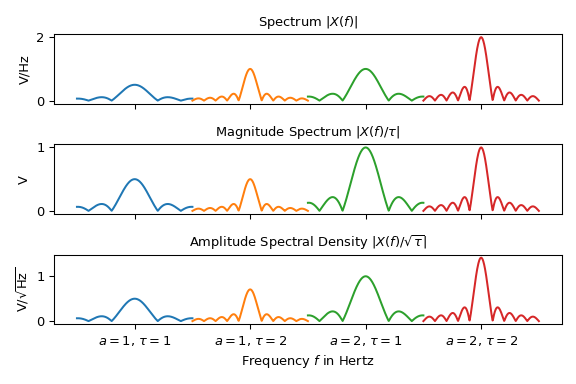
Beachten Sie, dass je nach Darstellung die Höhe der Spitzen variiert. Nur die Interpretation des Betragsspektrums ist eindeutig: Die Spitze bei \(f_x\) im zweiten Diagramm repräsentiert die halbe Amplitude \(|a|\) des Sinussignals. Bei allen anderen Darstellungen muss die Dauer \(\tau\) berücksichtigt werden, um Informationen über die Amplitude des Signals zu extrahieren.

Abgetastetes Sinussignal

In der Praxis werden abgetastete Signale häufig verwendet. D.h., das Signal wird durch \(n\) Abtastwerte \(x_k := x(kT)\), \(k=0, \ldots, n-1\) dargestellt, wobei \(T\) das Abtastintervall, \(\tau:=nT\) die Signaldauer und \(f_S := 1/T\) die Abtastfrequenz ist. Beachten Sie, dass das kontinuierliche Signal auf \([-f_S/2, f_S/2]\) bandbegrenzt sein muss, um Aliasing zu vermeiden, wobei \(f_S/2\) die Nyquistfrequenz genannt wird. [5] Das Ersetzen des Integrals durch eine Summe zur Berechnung von Energie und Leistung des Signals, d.h.

\[E_x = T\sum_{k=0}^{n-1} \abs{x_k}^2 = \frac{1}{2}|a|^2\tau\ , \qquad P_x = \frac{1}{\tau}E_x = \frac{1}{2}|a|^2\ ,\]

liefert dasselbe Ergebnis wie im kontinuierlichen Zeitfall von Gl. (2). Die diskrete Fourier-Transformation (DFT) und ihre Inverse (wie sie mit effizienten FFT-Berechnungen im Modul scipy.fft implementiert ist) sind gegeben durch

(6)\[X_l := \sum_{k=0}^{n-1} x_k \e^{-2\jj\pi k l / n}\ ,\qquad x_k = \frac{1}{n} \sum_{l=0}^{n-1} X_l \e^{2\jj\pi k l / n}\ .\]

Die DFT kann als eine unskalierte abgetastete Version der kontinuierlichen Fourier-Transformation aus Gl. (3) interpretiert werden, d.h.

\[X(l\Delta f) = T X_l\ , \quad \Delta f := 1/\tau = 1/(nT)\ .\]

Das folgende Diagramm zeigt das Betragsspektrum von zwei Sinussignalen mit Einheitsamplitude und Frequenzen von 20 Hz und 20,5 Hz. Das Signal besteht aus \(n=100\) Abtastwerten mit einem Abtastintervall von \(T=10\) ms, was zu einer Dauer von \(\tau=1\) s und einer Abtastfrequenz von \(f_S=100\) Hz führt.

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq

n, T = 100, 0.01  # number of samples and sampling interval
fcc = (20, 20.5)  # frequencies of sines
t = np.arange(n) * T
xx = (np.sin(2 * np.pi * fx_ * t) for fx_ in fcc)  # sine signals

f = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_) / n for x_ in xx)  # one-sided magnitude spectrum

fg1, ax1 = plt.subplots(1, 1, tight_layout=True, figsize=(6., 3.))
ax1.set(title=r"Magnitude Spectrum (no window) of $x(t) = \sin(2\pi f_x t)$ ",
        xlabel=rf"Frequency $f$ in Hertz (bin width $\Delta f = {f[1]}\,$Hz)",
        ylabel=r"Magnitude $|X(f)|/\tau$", xlim=(f[0], f[-1]))
for X_, fc_, m_ in zip(XX, fcc, ('x-', '.-')):
    ax1.plot(f, abs(X_), m_, label=rf"$f_x={fc_}\,$Hz")

ax1.grid(True)
ax1.legend()
plt.show()

Die Interpretation des 20-Hz-Signals scheint unkompliziert: Alle Werte sind null, außer bei 20 Hz. Dort ist es 0,5, was der halben Amplitude des Eingangssignals gemäß Gl. (1) entspricht. Die Spitze des 20,5-Hz-Signals ist dagegen über die Frequenzachse verteilt. Gl. (3) zeigt, dass dieser Unterschied darauf zurückzuführen ist, dass 20 Hz ein Vielfaches der Bin-Breite von 1 Hz ist, während 20,5 Hz dies nicht ist. Das folgende Diagramm verdeutlicht dies, indem das kontinuierliche Spektrum über das abgetastete gelegt wird

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq

n, T = 100, 0.01  # number of samples and sampling interval
tau = n*T
t = np.arange(n) * T
fcc = (20, 20.5)  # frequencies of sines
xx = (np.sin(2 * np.pi * fc_ * t) for fc_ in fcc)  # sine signals

f = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_) / n for x_ in xx)  # one-sided FFT normalized to magnitude

i0, i1 = 15, 25
f_cont = np.linspace(f[i0], f[i1], 501)

fg1, axx = plt.subplots(1, 2, sharey='all', tight_layout=True,
                        figsize=(6., 3.))
for c_, (ax_, X_, fx_) in enumerate(zip(axx, XX, fcc)):
    Xc_ = (np.sinc(tau * (f_cont - fx_)) +
           np.sinc(tau * (f_cont + fx_))) / 2
    ax_.plot(f_cont, abs(Xc_), f'-C{c_}', alpha=.5, label=rf"$f_x={fx_}\,$Hz")
    m_line, _, _, = ax_.stem(f[i0:i1+1], abs(X_[i0:i1+1]), markerfmt=f'dC{c_}',
                             linefmt=f'-C{c_}', basefmt=' ')
    plt.setp(m_line, markersize=5)

    ax_.legend(loc='upper left', frameon=False)
    ax_.set(xlabel="Frequency $f$ in Hertz", xlim=(f[i0], f[i1]),
            ylim=(0, 0.59))

axx[0].set(ylabel=r'Magnitude $|X(f)/\tau|$')
fg1.suptitle("Continuous and Sampled Magnitude Spectrum ", x=0.55, y=0.93)
fg1.tight_layout()
plt.show()

Dass eine leichte Frequenzvariation zu deutlich unterschiedlich aussehenden Betragsspektren führt, ist offensichtlich ein unerwünschtes Verhalten für viele praktische Anwendungen. Die folgenden beiden gängigen Techniken können zur Verbesserung eines Spektrums eingesetzt werden

Die sogenannte "Zero-Padding" verringert \(\Delta f\), indem Nullen am Ende des Signals angehängt werden. Um die Frequenz q-mal zu übersampeln, übergeben Sie den Parameter n=q*n_x an die Funktion fft / rfft, wobei n_x die Länge des Eingangssignals ist.

Die zweite Technik wird als Windowing bezeichnet, d.h. die Multiplikation des Eingangssignals mit einer geeigneten Funktion, die typischerweise die Nebenkeulen auf Kosten der Verbreiterung der Hauptkeule unterdrückt. Die gewichtete DFT kann ausgedrückt werden als

(7)\[X^w_l := \sum_{k=0}^{n-1} x_k w_k\e^{-2\jj\pi k l / n}\ ,\]

wobei \(w_k\), \(k=0,\ldots,n-1\) die abgetastete Fensterfunktion ist. Um die abgetasteten Versionen der im vorherigen Unterabschnitt gegebenen Spektraldarstellungen zu berechnen, müssen die folgenden Normierungskonstanten

\[c^\text{amp}:= \abs{\sum_{k=0}^{n-1} w_k}\ ,\qquad c^\text{den} := \sqrt{\sum_{k=0}^{n-1} \abs{w_k}^2}\]

verwendet werden. Die erste stellt sicher, dass eine Spitze im Spektrum mit der Amplitude des Signals bei dieser Frequenz übereinstimmt. Z.B. kann das Betragsspektrum ausgedrückt werden als \(|X^w_l / c^\text{amp}|\). Die zweite Konstante garantiert, dass die Leistung eines Frequenzintervalls, wie in Gl. (5) definiert, übereinstimmt. Die Absolutwerte werden benötigt, da komplexwertige Fenster nicht verboten sind.

Das folgende Diagramm zeigt das Ergebnis der Anwendung eines hann-Fensters und dreifacher Übersampling auf \(x(t)\)

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq
from scipy.signal.windows import hann

n, T = 100, 0.01  # number of samples and sampling interval
tau = n*T
q = 3  # over-sampling factor
t = np.arange(n) * T
fcc = (20, 20.5)  # frequencies of sines
xx = [np.sin(2 * np.pi * fc_ * t) for fc_ in fcc]  # sine signals
w = hann(n)
c_w = abs(sum(w))  # normalize constant for window

f_X = rfftfreq(n, T)  # frequency bins range from 0 Hz to Nyquist freq.
XX = (rfft(x_ * w) / c_w for x_ in xx)  # one-sided amplitude spectrum
# Oversampled spectrum:
f_Y = rfftfreq(n*q, T)  # frequency bins range from 0 Hz to Nyquist freq.
YY = (rfft(x_ * w, n=q*n) / c_w for x_ in xx)  # one-sided magnitude spectrum

i0, i1 = 15, 25
j0, j1 = i0*q, i1*q

fg1, axx = plt.subplots(1, 2, sharey='all', tight_layout=True,
                        figsize=(6., 3.))
for c_, (ax_, X_, Y_, fx_) in enumerate(zip(axx, XX, YY, fcc)):
    ax_.plot(f_Y[j0:j1 + 1], abs(Y_[j0:j1 + 1]), f'.-C{c_}',
             label=rf"$f_x={fx_}\,$Hz")
    m_ln, s_ln, _, = ax_.stem(f_X[i0:i1 + 1], abs(X_[i0:i1 + 1]), basefmt=' ',
                              markerfmt=f'dC{c_}', linefmt=f'-C{c_}')
    plt.setp(m_ln, markersize=5)
    plt.setp(s_ln, alpha=0.5)

    ax_.legend(loc='upper left', frameon=False)
    ax_.set(xlabel="Frequency $f$ in Hertz", xlim=(f_X[15], f_X[25]),
            ylim=(0, 0.59))

axx[0].set(ylabel=r'Magnitude $|X(f)/\tau|$')
fg1.suptitle(rf"Magnitude Spectrum (Hann window, ${q}\times$oversampled)",
             x=0.55, y=0.93)
plt.show()

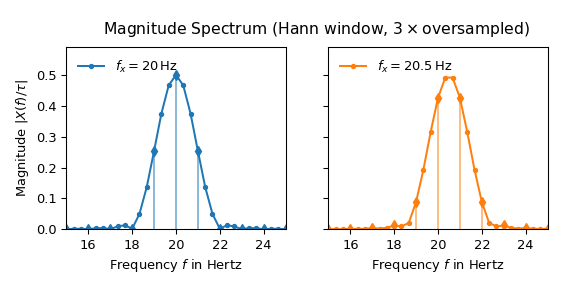
Nun sehen beide Keulen fast identisch aus und die Seitenkeulen sind gut unterdrückt. Die maximale Amplitude des 20,5-Hz-Spektrums liegt ebenfalls sehr nahe an der erwarteten Höhe von einem halben.

Spektralenergie und Spektralleistung können analog zu Gl. (4) berechnet werden, was zu identischen Ergebnissen führt, d.h.

\[E^w_X = T\sum_{k=0}^{n-1} \abs{\frac{X^w_k}{c^\text{den}}}^2 = E_x\ ,\qquad P^w_X = \frac{1}{\tau} E^w_X = \frac{1}{n} \sum_{k=0}^{n-1} \abs{\frac{X^w_k}{c^\text{den}}}^2 = P_x\ .\]

Diese Formulierung ist nicht zu verwechseln mit dem Spezialfall eines Rechteckfensters (oder ohne Fenster), d.h. \(w_k = 1\), \(X^w_l=X_l\), \(c^\text{den}=\sqrt{n}\), was zu

\[E_X = \frac{T}{n}\sum_{k=0}^{n-1} \abs{X_k}^2\ ,\qquad P_X = \frac{1}{n^2} \sum_{k=0}^{n-1} \abs{X_k}^2\ .\]

führt. Die gewichtete frequenzdiskrete Leistungsdichtespektrum

\[S^w_{xx} := \frac{1}{f_S}\abs{\frac{X^w_l}{c^\text{den}}}^2 = T \abs{\frac{X^w_l}{c^\text{den}}}^2\]

ist im Frequenzbereich \([0, f_S)\) definiert und kann als Leistung pro Frequenzintervall \(\Delta f\) interpretiert werden. Die Integration über ein Frequenzband \([l_a\Delta f, l_b\Delta f)\), wie in Gl. (5), wird zur Summe

\[P_X^{a,b} = \Delta f\sum_{k=l_a}^{l_b-1} S^w_{xx} = \frac{1}{nT}\sum_{k=l_a}^{l_b-1} S^w_{xx}\ .\]

Die gewichtete frequenzdiskrete Energiespektraldichte \(\tau S^w_{xx}\) kann analog definiert werden.

Die obige Diskussion zeigt, dass abgetastete Versionen der Spektraldarstellungen wie im kontinuierlichen Zeitfall definiert werden können. Die folgende Tabelle fasst diese zusammen

Vergleich von Spektraldarstellungen einer gewichteten DFT \(X^w_l\) aus Gl. (7) für ein abgetastetes Signal mit Einheit \(\text{V}\):

	Spektrum	Amplitudenspektrum	Energiespektraldichte	Leistungsdichtespektrum (PSD)	Amplitudenspektraldichte
Definition	\(\tau X^w_l / c^\text{amp}\)	\(X^w_l / c^\text{amp}\)	\(\tau T |X^w_l / c^\text{den}|^2\)	\(T |X^w_l / c^\text{den}|^2\)	\(\sqrt{T} X^w_l / c^\text{den}\)
Einheit	\(\text{V} / \text{Hz}\)	\(\text{V}\)	\(\text{V}^2\text{s} / \text{Hz}\)	\(\text{V}^2 / \text{Hz}\)	\(\text{V} / \sqrt{\text{Hz}}\)

Beachten Sie, dass bei den Dichten die Amplitudenwerte bei \(\pm f_x\) von den Werten im kontinuierlichen Zeitfall abweichen, da die Umstellung von Integration auf Summation zur Bestimmung der Spektralenergie/-leistung erfolgt.

Obwohl das Hann-Fenster die gebräuchlichste Fensterfunktion in der Spektralanalyse ist, gibt es auch andere Fenster. Das folgende Diagramm zeigt das Betragsspektrum verschiedener Fensterfunktionen aus dem Untermodul windows. Es kann als die Keulenform eines Einfrequenzsignals interpretiert werden. Beachten Sie, dass nur die rechte Hälfte gezeigt wird und die \(y\)-Achse in Dezibel skaliert ist, d.h. logarithmisch skaliert.

import matplotlib.pyplot as plt
import numpy as np

from scipy.fft import rfft, rfftfreq
from scipy.signal import get_window

n, n_zp = 128, 16384  # number of samples without and with zero-padding
t = np.arange(n)
f = rfftfreq(n_zp, 1 / n)

ww = ['boxcar', 'hann', 'hamming', 'tukey', 'blackman', 'flattop']
fg0, axx = plt.subplots(len(ww), 1, sharex='all', sharey='all', figsize=(6., 4.))
for c_, (w_name_, ax_) in enumerate(zip(ww, axx)):
    w_ = get_window(w_name_, n, fftbins=False)
    W_ = rfft(w_ / abs(sum(w_)), n=n_zp)
    W_dB = 20*np.log10(np.maximum(abs(W_), 1e-250))
    ax_.plot(f, W_dB, f'C{c_}-', label=w_name_)
    ax_.text(0.1, -50, w_name_, color=f'C{c_}', verticalalignment='bottom',
             horizontalalignment='left', bbox={'color': 'white', 'pad': 0})
    ax_.set_yticks([-20, -60])
    ax_.grid(axis='x')

axx[0].set_title("Spectral Leakage of various Windows")
fg0.supylabel(r"Normalized Magnitude $20\,\log_{10}|W(f)/c^\operatorname{amp}|$ in dB",
              x=0.04, y=0.5, fontsize='medium')
axx[-1].set(xlabel=r"Normalized frequency $f/\Delta f$ in bins",
            xlim=(0, 9), ylim=(-75, 3))

fg0.tight_layout(h_pad=0.4)
plt.show()

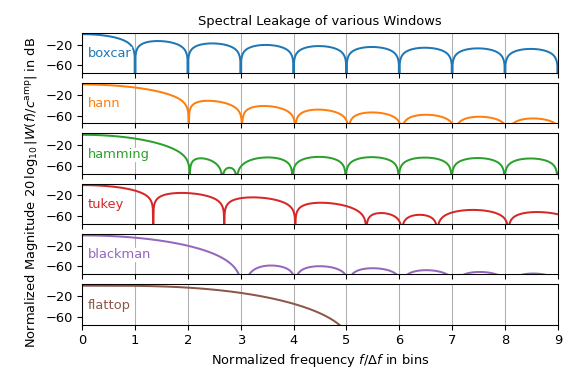
Dieses Diagramm zeigt, dass die Wahl der Fensterfunktion typischerweise ein Kompromiss zwischen der Breite der Hauptkeulen und der Höhe der Seitenkeulen ist. Beachten Sie, dass das boxcar-Fenster einer \(\rect\)-Funktion entspricht, d.h. keiner Fensterung. Darüber hinaus werden viele der dargestellten Fenster häufiger in der Filterentwicklung als in der Spektralanalyse verwendet.

Phase des Spektrums

Die Phase (d. h. die angle) der Fourier-Transformation wird typischerweise zur Untersuchung der Zeitverzögerung der Spektralkomponenten eines Signals verwendet, das ein System wie einen Filter durchläuft. Im folgenden Beispiel wird das Standard-Testsignal, ein Impuls mit Einheitsleistung, durch einen einfachen Filter geleitet, der die Eingabe um drei Abtastungen verzögert. Die Eingabe besteht aus \(n=50\) Abtastungen mit dem Abtastintervall \(T = 1\) s. Die Darstellung zeigt Betrag und Phase über die Frequenz des Ein- und Ausgangssignals

import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import numpy as np

from scipy import signal
from scipy.fft import rfft, rfftfreq

# Create input signal:
n = 50
x = np.zeros(n)
x[0] = n

# Apply FIR filter which delays signal by 3 samples:
y = signal.lfilter([0, 0, 0, 1], 1, x)

X, Y = (rfft(z_) / n for z_ in (x, y))
f = rfftfreq(n, 1)  # sampling interval T = 1 s

fig = plt.figure(tight_layout=True, figsize=(6., 4.))
gs = gridspec.GridSpec(3, 1)
ax0 = fig.add_subplot(gs[0, :])
ax1 = fig.add_subplot(gs[1:, :], sharex=ax0)

for Z_, n_, m_ in zip((X, Y), ("Input $X(f)$", "Output $Y(f)$"), ('+-', 'x-')):
    ax0.plot(f, abs(Z_), m_, alpha=.5, label=n_)
    ax1.plot(f, np.unwrap(np.angle(Z_)), m_, alpha=.5, label=n_)

ax0.set(title="Frequency Response of 3 Sample Delay Filter (no window)",
        ylabel="Magnitude", xlim=(0, f[-1]), ylim=(0, 1.1))
ax1.set(xlabel=rf"Frequency $f$ in Hertz ($\Delta f = {1/n}\,$Hz)",
        ylabel=r"Phase in rad")
ax1.set_yticks(-np.arange(0, 7)*np.pi/2,
               ['0', '-π/2', '-π', '-3/2π', '-2π', '-4/3π', '-3π'])

ax2 = ax1.twinx()
ax2.set(ylabel=r"Phase in Degrees", ylim=np.rad2deg(ax1.get_ylim()),
        yticks=np.arange(-540, 90, 90))
for ax_ in (ax0, ax1):
    ax_.legend()
    ax_.grid()
plt.show()

Die Eingabe hat einen Einheitsbetrag und eine Nulphasen-Fourier-Transformation, was der Grund für ihre Verwendung als Testsignal ist. Die Ausgabe hat ebenfalls einen Einheitsbetrag, aber eine linear abfallende Phase mit einer Steigung von \(-6\pi\). Dies ist zu erwarten, da die Verzögerung eines Signals \(x(t)\) um \(\Delta t\) einen zusätzlichen linearen Phasen-Term in seiner Fourier-Transformation erzeugt, d.h.:

\[\int_\IR x(t-\Delta t) \e^{-\jj2\pi f t}\dd t = X(f)\, e^{-\jj2\pi \Delta t f}\ .\]

Beachten Sie, dass die Phase in der Darstellung nicht auf das Intervall \((+\pi, \pi]\) (Ausgabe von angle) beschränkt ist und daher keine Diskontinuitäten aufweist. Dies wird durch die Verwendung der Funktion numpy.unwrap erreicht. Wenn die Übertragungsfunktion des Filters bekannt ist, kann freqz verwendet werden, um die spektrale Antwort eines Filters direkt zu bestimmen.

Spektren mit Mittelung

Die Funktion periodogram berechnet eine Leistungsdichtespektrum (scaling='density') oder ein quadriertes Betragsspektrum (scaling='spectrum'). Um ein geglättetes Periodogramm zu erhalten, kann die Funktion welch verwendet werden. Sie glättet, indem das Eingangssignal in überlappende Segmente unterteilt und dann die Fenster-DFT jedes Segments berechnet wird. Das Ergebnis ist der Durchschnitt dieser DFTs.

Das folgende Beispiel zeigt das quadrierte Betragsspektrum und die Leistungsdichtespektrum eines Signals, das aus einem \(1,27\,\text{kHz}\)-Sinussignal mit der Amplitude \(\sqrt{2}\,\text{V}\) und additivem Gauß'schem Rauschen mit einer spektralen Leistungsdichte mit einem Mittelwert von \(10^{-3}\,\text{V}^2/\text{Hz}\) besteht.

import matplotlib.pyplot as plt
import numpy as np
import scipy.signal as signal

rng = np.random.default_rng(73625)  # seeding for reproducibility

fs, n = 10e3, 10_000
f_x, noise_power = 1270, 1e-3 * fs / 2
t = np.arange(n) / fs
x = (np.sqrt(2) * np.sin(2 * np.pi * f_x * t) +
     rng.normal(scale=np.sqrt(noise_power), size=t.shape))

fg, axx = plt.subplots(1, 2, sharex='all', tight_layout=True, figsize=(7, 3.5))
axx[0].set(title="Squared Magnitude Spectrum", ylabel="Square of Magnitude in V²")
axx[1].set(title="Power Spectral Density", ylabel="Power Spectral Density in V²/Hz")
for ax_, s_ in zip(axx, ('spectrum', 'density')):
    f_p, P_p = signal.periodogram(x, fs, 'hann', scaling=s_)
    f_w, P_w = signal.welch(x, fs, scaling=s_)
    ax_.semilogy(f_p/1e3, P_p, label=f"Periodogram ({len(f_p)} bins)")
    ax_.semilogy(f_w/1e3, P_w, label=f"Welch's Method ({len(f_w)} bins)")
    ax_.set(xlabel="Frequency in kHz", xlim=(0, 2), ylim=(1e-7, 1.3))
    ax_.grid(True)
    ax_.legend(loc='lower center')
plt.show()

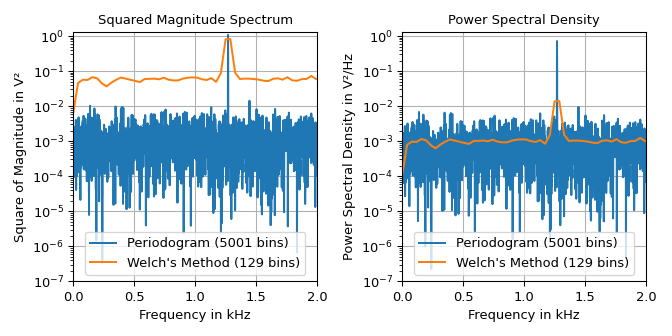
Die Darstellungen zeigen, dass die Funktion welch einen viel glatteren Rauschboden auf Kosten der Frequenzauflösung erzeugt. Aufgrund der Glättung ist die Höhe des Sinus-Lobes breiter und nicht so hoch wie im Periodogramm. Die linke Darstellung kann verwendet werden, um die Höhe des Lobes abzulesen, d. h. die halbe quadrierte Betragsgröße des Sinus von \(1\,\text{V}^2\). Die rechte Darstellung kann verwendet werden, um den Rauschboden von \(10^{-3}\,\text{V}^2/\text{Hz}\) zu bestimmen. Beachten Sie, dass die Lobe-Höhe des gemittelten quadrierten Betragsspektrums aufgrund der begrenzten Frequenzauflösung nicht genau eins ist. Entweder Null-Padding (z. B. Übergabe von nfft=4*len(x) an welch) oder die Reduzierung der Anzahl der Segmente durch Erhöhung der Segmentlänge (Einstellung des Parameters nperseg) könnten verwendet werden, um die Anzahl der Frequenzbänder zu erhöhen.

Lomb-Scargle-Periodogramme (lombscargle)

Die Methode der kleinsten Quadrate zur Spektralanalyse (Least-Squares Spectral Analysis, LSSA) [6] [7] ist eine Methode zur Schätzung eines Frequenzspektrums, die auf einer Anpassung von Sinusoiden an Datenpunkte nach der Methode der kleinsten Quadrate basiert, ähnlich der Fourier-Analyse. Die Fourier-Analyse, die am häufigsten verwendete Spektralmethode in der Wissenschaft, verstärkt im Allgemeinen langperiodische Rauschen in lückenhaften Aufzeichnungen; LSSA mildert solche Probleme.

Die Lomb-Scargle-Methode führt eine Spektralanalyse an ungleichmäßig abgetasteten Daten durch und ist bekannt dafür, ein leistungsfähiges Mittel zur Suche und Signifikanzprüfung schwacher periodischer Signale zu sein.

Für eine Zeitreihe, die \(N_{t}\) Messungen \(X_{j}\equiv X(t_{j})\) zu Zeiten \(t_{j}\) umfasst, wobei \((j = 1, \ldots, N_{t})\), angenommen wird, dass sie skaliert und verschoben wurde, sodass ihr Mittelwert Null und ihre Varianz Eins ist, ist das normalisierte Lomb-Scargle-Periodogramm bei der Frequenz \(f\):

\[P_{n}(f) = \frac{1}{2}\left\{\frac{\left[\sum_{j}^{N_{t}}X_{j}\cos\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\cos^{2}\omega(t_{j}-\tau)}+\frac{\left[\sum_{j}^{N_{t}}X_{j}\sin\omega(t_{j}-\tau)\right]^{2}}{\sum_{j}^{N_{t}}\sin^{2}\omega(t_{j}-\tau)}\right\}.\]

Hier ist \(\omega \equiv 2\pi f\) die Winkelfrequenz. Der frequenzabhängige Zeitversatz \(\tau\) ist gegeben durch

\[\tan 2\omega\tau = \frac{\sum_{j}^{N_{t}}\sin 2\omega t_{j}}{\sum_{j}^{N_{t}}\cos 2\omega t_{j}}.\]

Die Funktion lombscargle berechnet das Periodogramm mit einem leicht modifizierten Algorithmus von Zechmeister und Kürster [8], der die Gewichtung einzelner Abtastwerte und die Berechnung eines unbekannten Versatzes (auch "gleitender Mittelwert" genannt) für jede Frequenz unabhängig ermöglicht.

Kurzzeit-Fourier-Transformation

Dieser Abschnitt gibt einige Hintergrundinformationen zur Verwendung der Klasse ShortTimeFFT: Die Kurzzeit-Fourier-Transformation (STFT) kann zur Analyse der spektralen Eigenschaften von Signalen über die Zeit verwendet werden. Sie teilt ein Signal in überlappende Blöcke auf, indem ein gleitendes Fenster verwendet wird, und berechnet die Fourier-Transformation jedes Blocks. Für ein kontinuierliches komplexwertiges Signal \(x(t)\) ist die STFT [9] definiert als

\[S(f, t) := \int_\IR x(\xi)\, \conj{w(\xi-t)}\,\e^{-\jj2\pi f \xi}\dd\xi\ ,\]

wobei \(w(t)\) eine komplexwertige Fensterfunktion ist, deren komplexes Konjugat \(\conj{w(t)}\) ist. Sie kann als Bestimmung des Skalarprodukts von \(x\) mit dem Fenster \(w\) interpretiert werden, das um die Zeit \(t\) verschoben und dann durch die Frequenz \(f\) moduliert (d.h. frequenzverschoben) wird. Für die Arbeit mit abgetasteten Signalen \(x[k] := x(kT)\), \(k\in\IZ\), mit dem Abtastintervall \(T\) (dem Kehrwert der Abtastfrequenz fs) muss die diskrete Version, d. h. die Auswertung der STFT nur an diskreten Gitterpunkten \(S[q, p] := S(q \Delta f, p\Delta t)\), \(q,p\in\IZ\), verwendet werden. Sie kann formuliert werden als

(8)\[S[q,p] = \sum_{k=0}^{N-1} x[k]\,\conj{w[k-p h]}\, \e^{-\jj2\pi q k / N}\ , \quad q,p\in\IZ\ ,\]

wobei p den Zeitindex von \(S\) mit dem Zeitintervall \(\Delta t := h T\), \(h\in\IN\) (siehe delta_t), darstellt, was als hop-Größe von \(h\) Abtastungen ausgedrückt werden kann. \(q\) stellt den Frequenzindex von \(S\) mit der Schrittweite \(\Delta f := 1 / (N T)\) (siehe delta_f) dar, was sie FFT-kompatibel macht. \(w[m] := w(mT)\), \(m\in\IZ\) ist die abgetastete Fensterfunktion.

Um der Implementierung von ShortTimeFFT besser zu entsprechen, ist es sinnvoll, Gl. (8) als zweistufigen Prozess neu zu formulieren:

1. Extrahieren Sie das \(p\)-te Slice durch Fensterung mit dem Fenster \(w[m]\), das aus \(M\) Abtastwerten besteht (siehe m_num) und zentriert bei \(t[p] := p \Delta t = h T\) ist (siehe delta_t), d. h.:

   (9)\[x_p[m] = x\!\big[m - \lfloor M/2\rfloor + h p\big]\, \conj{w[m]}\ , \quad m = 0, \ldots M-1\ ,\]

   wobei die ganze Zahl \(\lfloor M/2\rfloor\) M//2 darstellt, d. h. es ist der Mittelpunkt des Fensters (m_num_mid). Der Einfachheit halber wird angenommen, dass \(x[k]:=0\) für \(k\not\in\{0, 1, \ldots, N-1\}\) gilt. Im Unterabschnitt Sliding Windows wird die Indizierung der Slices detaillierter besprochen.

2. Führen Sie dann eine diskrete Fourier-Transformation (d. h. eine FFT) von \(x_p[m]\) durch.

   (10)\[S[q, p] = \sum_{m=0}^{M-1} x_p[m] \exp\!\big\{% -2\jj\pi (q + \phi_m)\, m / M\big\}\ .\]

   Beachten Sie, dass eine lineare Phase \(\phi_m\) (siehe phase_shift) spezifiziert werden kann, was einer Verschiebung der Eingabe um \(\phi_m\) Abtastungen entspricht. Der Standardwert ist \(\phi_m = \lfloor M/2\rfloor\) (entspricht per Definition phase_shift = 0), was lineare Phasenkomponenten für unverschobene Signale unterdrückt. Darüber hinaus kann die FFT durch Auffüllen von \(w[m]\) mit Nullen überabgetastet werden. Dies kann durch Angabe von mfft, das größer als die Fensterlänge m_num ist, erreicht werden - dies setzt \(M\) auf mfft (was impliziert, dass auch \(w[m]:=0\) für \(m\not\in\{0, 1, \ldots, M-1\}\) gilt).

Die inverse Kurzzeit-Fourier-Transformation (istft) wird durch Umkehrung dieser beiden Schritte implementiert:

1. Führen Sie die inverse diskrete Fourier-Transformation durch, d. h.:

   \[x_p[m] = \frac{1}{M}\sum_{q=0}^M S[q, p]\, \exp\!\big\{ 2\jj\pi (q + \phi_m)\, m / M\big\}\ .\]

2. Summieren Sie die verschobenen Slices, gewichtet mit \(w_d[m]\), um das ursprüngliche Signal zu rekonstruieren, d. h.:

   \[x[k] = \sum_p x_p\!\big[\mu_p(k)\big]\, w_d\!\big[\mu_p(k)\big]\ ,\quad \mu_p(k) = k + \lfloor M/2\rfloor - h p\]

   für \(k \in [0, \ldots, n-1]\). \(w_d[m]\) ist das sogenannte duale Fenster von \(w[m]\) und besteht ebenfalls aus \(M\) Abtastwerten.

Beachten Sie, dass eine inverse STFT nicht unbedingt für alle Fenster und Hop-Größen existiert. Für ein gegebenes Fenster \(w[m]\) muss die Hop-Größe \(h\) klein genug sein, um sicherzustellen, dass jedes Abtastwert von \(x[k]\) von einem Nicht-Null-Wert von mindestens einem Fenster-Slice berührt wird. Dies wird manchmal als "Nicht-Null-Überlappungsbedingung" bezeichnet (siehe check_NOLA). Weitere Details finden Sie im Unterabschnitt Inverse STFT und Duale Fenster.

Gleitende Fenster

Dieser Unterabschnitt erläutert die Indizierung des gleitenden Fensters in ShortTimeFFT anhand eines Beispiels: Betrachten Sie ein Fenster der Länge 6 mit einem hop-Intervall von zwei und einem Abtastintervall T von eins, z. B. ShortTimeFFT (np.ones(6), 2, fs=1). Die folgende Abbildung stellt schematisch die ersten vier Fensterpositionen dar, die auch als Zeitscheiben bezeichnet werden.

Die x-Achse bezeichnet die Zeit \(t\), die dem Abtastindex k entspricht, der durch die untere Reihe von blauen Kästen angezeigt wird. Die y-Achse bezeichnet den Index der Zeitscheibe \(p\). Das Signal \(x[k]\) beginnt bei Index \(k=0\) und ist durch einen hellblauen Hintergrund gekennzeichnet. Per Definition ist die Null-Scheibe (\(p=0\)) bei \(t=0\) zentriert. Die Mitte jeder Scheibe (m_num_mid), hier die Abtastung 6//2=3, ist mit dem Text "mid" markiert. Standardmäßig berechnet stft alle Scheiben, die eine Überlappung mit dem Signal haben. Daher befindet sich die erste Scheibe bei p_min = -1 mit dem niedrigsten Abtastindex k_min = -5. Der erste Abtastindex, der von einer nicht nach links aus dem Signal ragenden Scheibe nicht betroffen ist, ist \(p_{lb} = 2\) und der erste Abtastindex, der von Grenzwert-Effekten nicht betroffen ist, ist \(k_{lb} = 5\). Die Eigenschaft lower_border_end gibt das Tupel \((k_{lb}, p_{lb})\) zurück.

Das Verhalten am Ende des Signals wird für ein Signal mit \(n=50\) Abtastwerten unten dargestellt, wie durch den blauen Hintergrund angezeigt.

Hier hat die letzte Scheibe den Index \(p=26\). Daher bedeutet p_max = 27 die erste Scheibe, die das Signal nicht berührt (gemäß der Python-Konvention, dass der Endindex außerhalb des Bereichs liegt). Der entsprechende Abtastindex ist k_max = 55. Die erste Scheibe, die nach rechts übersteht, ist \(p_{ub} = 24\) mit ihrer ersten Abtastung bei \(k_{ub}=45\). Die Funktion upper_border_begin gibt das Tupel \((k_{ub}, p_{ub})\) zurück.

Inverse STFT und duale Fenster

Der Begriff duales Fenster stammt aus der Rahmentheorie [10], wo ein Rahmen eine Reihenentwicklung ist, die jede Funktion in einem gegebenen Hilbertraum darstellen kann. Dort sind die Entwicklungen \(\{g_k\}\) und \(\{h_k\}\) duale Rahmen, wenn für alle Funktionen \(f\) im gegebenen Hilbertraum \(\mathcal{H}\) gilt:

\[f = \sum_{k\in\IN} \langle f, g_k\rangle h_k = \sum_{k\in\IN} \langle f, h_k\rangle g_k\ , \quad f \in \mathcal{H}\ ,\]

wobei \(\langle ., .\rangle\) das Skalarprodukt von \(\mathcal{H}\) bezeichnet. Alle Rahmen haben duale Rahmen [10].

Eine STFT, die nur an diskreten Gitterpunkten \(S(q \Delta f, p\Delta t)\) ausgewertet wird, wird in der Literatur als "Gabor-Rahmen" bezeichnet [9] [10]. Da die Unterstützung des Fensters \(w[m]\) auf ein endliches Intervall beschränkt ist, fällt die ShortTimeFFT in die Klasse der sogenannten "painless non-orthogonal expansions" [9]. In diesem Fall haben die dualen Fenster immer die gleiche Unterstützung und können durch Invertierung einer Diagonalmatrix berechnet werden. Eine grobe Herleitung, die nur ein gewisses Verständnis der Matrixmanipulation erfordert, wird im Folgenden skizziert.

Da die STFT in Gl. (8) eine lineare Abbildung in \(x[k]\) ist, kann sie in Vektor-Matrix-Notation ausgedrückt werden. Dies ermöglicht es uns, die Umkehrung durch die formale Lösung der linearen Methode der kleinsten Quadrate (wie in lstsq) auszudrücken, was zu einem schönen und einfachen Ergebnis führt.

Wir beginnen damit, die Fensterung von Gl. (9) neu zu formulieren.

(11)\[\begin{split} \vb{x}_p = \vb{W}_{\!p}\,\vb{x} = \begin{bmatrix} \cdots & 0 & w[0] & 0 & \cdots&&&\\ & \cdots & 0 & w[1] & 0 & \cdots&&\\ & & & & \ddots&&&\\ &&\cdots & 0 & 0 & w[M-1] & 0 & \cdots \end{bmatrix}\begin{bmatrix} x[0]\\ x[1]\\ \vdots\\ x[N-1] \end{bmatrix} ,\end{split}\]

wobei die \(M\times N\) Matrix \(\vb{W}_{\!p}\) nur von Null verschiedene Einträge auf der \((ph)\)-ten Nebendiagonalen hat, d. h.:

(12)\[\begin{split} W_p[m,k] = w[m]\, \delta_{m+ph,k}\ ,\quad \delta_{k,l} &= \begin{cases} 1 & \text{ für } k=l\ ,\\ 0 & \text{ sonst ,} \end{cases}\end{split}\]

wobei \(\delta_{k,l}\) das Kronecker-Delta ist. Gl. (10) kann ausgedrückt werden als:

(13)\[\vb{s}_p = \vb{F}\,\vb{x}_p \quad\text{mit}\quad F[q,m] = \frac{1}{\sqrt{M}}\exp\!\big\{-2\jj\pi (q + \phi_m)\, m / M\big\}\ ,\]

was die STFT des \(p\)-ten Slices als

(14)\[\vb{s}_p = \vb{F}\vb{W}_{\!p}\,\vb{x} =: \vb{G}_p\,\vb{x} \quad\text{mit}\quad s_p[q] = S[p,q]\ .\]

ermöglicht. Aufgrund des Skalierungsfaktors \(M^{-1/2}\) ist \(\vb{F}\) unitär, d. h. die Inverse gleicht der konjugierten Transponierten, was bedeutet \(\conjT{\vb{F}}\vb{F} = \vb{I}\). Andere Skalierungen, z. B. wie in Gl. (6), sind ebenfalls zulässig, würden aber in diesem Abschnitt die Notation etwas komplizierter machen.

Um eine einzelne Vektor-Matrix-Gleichung für die STFT zu erhalten, werden die Slices zu einem Vektor zusammengefügt, d. h.:

\[\begin{split}\vb{s} := \begin{bmatrix} \vb{s}_0\\ \vb{s}_1\\ \vdots\\ \vb{s}_{P-1} \end{bmatrix} = \begin{bmatrix} \vb{G}_0\\ \vb{G}_1\\ \vdots\\ \vb{G}_{P-1} \end{bmatrix}\, \vb{x} =: \vb{G}\, \vb{x}\ ,\end{split}\]

wobei \(P\) die Anzahl der Spalten der resultierenden STFT ist. Um diese Gleichung umzukehren, kann die Moore-Penrose-Inverse \(\vb{G}^\dagger\) verwendet werden.

(15)\[\vb{x} = \inv{\conjT{\vb{G}}\vb{G}}\, \conjT{\vb{G}} \vb{s} =: \vb{G}^\dagger \vb{s}\ ,\]

die existiert, wenn

(16)\[\begin{split} \vb{D} := \conjT{\vb{G}}\vb{G} = \begin{bmatrix} \conjT{\vb{G}_0}& \conjT{\vb{G}_1}& \cdots & \conjT{\vb{G}_{P-1}} \end{bmatrix}^T \begin{bmatrix} \vb{G}_0\\ \vb{G}_1\\ \vdots\\ \vb{G}_{P-1} \end{bmatrix} = \sum_{p=0}^{P-1} \conjT{\vb{G}_p}\vb{G}_p \ .\end{split}\]

invertierbar ist. Dann gilt offensichtlich \(\vb{x} = \vb{G}^\dagger\vb{G}\,\vb{x} = \inv{\conjT{\vb{G}}\vb{G}}\,\conjT{\vb{G}}\vb{G}\,\vb{x}\). \(\vb{D}\) ist immer eine Diagonalmatrix mit nicht-negativen Diagonaleinträgen. Dies wird deutlich, wenn \(\vb{D}\) weiter zu

(17)\[\vb{D} = \sum_{p=0}^{P-1} \conjT{\vb{G}_p}\vb{G}_p = \sum_{p=0}^{P-1} \conjT{(\vb{F}\,\vb{W}_{\!p})}\, \vb{F}\,\vb{W}_{\!p} = \sum_{p=0}^{P-1} \conjT{\vb{W}_{\!p}}\vb{W}_{\!p} =: \sum_{p=0}^{P-1} \vb{D}_p\]

vereinfacht wird, da \(\vb{F}\) unitär ist. Darüber hinaus gilt:

(18)\[\begin{split}D_p[r,s] &= \sum_{m=0}^{M-1} \conj{W_p^T[r,m]}\,W_p[m,s] = \sum_{m=0}^{M-1} \left(\conj{w[m]}\, \delta_{m+ph,r}\right) \left(w[m]\, \delta_{m+ph,s}\right)\\ &= \sum_{m=0}^{M-1} \big|w[m]\big|^2\, \delta_{r,s}\, \delta_{r,m+ph}\ .\end{split}\]

zeigt, dass \(\vb{D}_p\) eine Diagonalmatrix mit nicht-negativen Einträgen ist. Daher behält die Summation von \(\vb{D}_p\) diese Eigenschaft bei. Dies ermöglicht eine weitere Vereinfachung von Gl. (15), d. h.:

(19)\[\begin{split}\vb{x} &= \vb{D}^{-1} \conjT{\vb{G}}\vb{s} = \sum_{p=0}^{P-1} \vb{D}^{-1}\conjT{\vb{W}_{\!p}}\, \conjT{\vb{F}}\vb{s}_p = \sum_{p=0}^{P-1} (\conj{\vb{W}_{\!p}\vb{D}^{-1}})^T\, \conjT{\vb{F}}\vb{s}_p\\ &=: \sum_{p=0}^{P-1}\conjT{\vb{U}_p}\,\conjT{\vb{F}}\vb{s}_p\ .\end{split}\]

Unter Verwendung von Gl. (12), (17), (18) kann \(\vb{U}_p=\vb{W}_{\!p}\vb{D}^{-1}\) ausgedrückt werden als

(20)\[\begin{split}U_p[m, k] &= W[m,k]\, D^{-1}[k,k] = \left(w[m] \delta_{m+ph,k}\right) \inv{\sum_{\eta=0}^{P-1} \vb{D}_\eta[k,k]} \delta_{m+ph,k}\\ &= w[m] \inv{\sum_{\eta=0}^{P-1}\sum_{\mu=0}^{M-1} \big|w[\mu]\big|^2\,\delta_{m+ph, \mu+\eta h}} \delta_{m+ph,k}\\ &= w[m] \inv{\sum_{\eta=0}^{P-1} \big|w[m+(p-\eta)h]\big|^2} \delta_{m+ph,k} \ .\end{split}\]

Dies zeigt, dass \(\vb{U}_p\) die gleiche Struktur wie \(\vb{W}_p\) in Gl. (12) hat, d. h. nur von Null verschiedene Einträge auf der \((ph)\)-ten Nebendiagonalen. Der Summenterm im Kehrwert kann als Verschieben von \(|w[\mu]|^2\) über \(w[m]\) (mit einer eingebauten Invertierung) interpretiert werden, sodass nur Komponenten, die mit \(w[m]\) überlappen, einen Effekt haben. Daher sind alle \(U_p[m, k]\), die weit genug vom Rand entfernt sind, identische Fenster. Um Randeffekte zu umgehen, wird \(x[k]\) mit Nullen aufgefüllt, wodurch \(\vb{U}\) vergrößert wird, sodass alle Slices, die \(x[k]\) berühren, das identische duale Fenster enthalten.

(21)\[\begin{split} w_d[m] &= w[m] \inv{\sum_{\eta\in\IZ} \big|w[m + \eta\, h]\big|^2}\\ &=\ w[m] \inv{\sum_{l=0}^{M-1} \big|w[l]\big|^2 \delta_{l+m,\eta h}}\ , \quad \eta\in \IZ\ .\end{split}\]

Da \(w[m] = 0\) für \(m \not\in\{0, \ldots, M-1\}\) gilt, muss nur über die Indizes \(\eta\) summiert werden, für die \(|\eta| < M/h\) gilt. Der zweite Ausdruck ist eine alternative Form, indem von Index \(l=0\) bis \(M\) in Schrittweiten von \(h\) summiert wird. \(\delta_{l+m,\eta h}\) ist die Kronecker-Delta-Schreibweise für (l+m) % h == 0. Der Name duales Fenster kann gerechtfertigt werden, indem Gl. (14) in Gl. (19) eingesetzt wird, d. h.:

(22)\[ \vb{x} = \sum_{p=0}^{P-1} \conjT{\vb{U}_p}\,\conjT{\vb{F}}\, \vb{F}\,\vb{W}_{\!p}\,\vb{x} = \left(\sum_{p=0}^{P-1} \conjT{\vb{U}_p}\,\vb{W}_{\!p}\right)\vb{x}\ ,\]

was zeigt, dass \(\vb{U}_p\) und \(\vb{W}_{\!p}\) vertauschbar sind. Da \(\vb{U}_p\) und \(\vb{W}_{\!p}\) die gleiche Struktur wie in Gl. (11) haben, enthält Gl. (22) eine allgemeine Bedingung für alle möglichen dualen Fenster, d. h.:

(23)\[\sum_{p=0}^{P-1} \conjT{\vb{W}_{\!p}}\,\vb{U}_p = \vb{I} \quad\Leftrightarrow\quad \sum_{p=0}^{P-1} \sum_{m=0}^{M-1} \conj{w[m]} u[m]\, \delta_{m+ph,i}\, \delta_{m+ph,j} = \delta_{i,j}\]

was umformuliert werden kann zu

(24)\[\conjT{\vb{V}}\,\vb{u} = \vb{1}\ , \qquad V[i,j] := w[i]\, \delta_{i, j+ph}\ , \qquad \vb{V}\in \IC^{M\times h},\ p\in\IZ\ ,\]

wobei \(\vb{1}\in\IR^h\) ein Einsenvektor ist. Der Grund, dass \(\vb{V}\) nur \(h\) Spalten hat, ist, dass die \(i\)-te und \((i+m)\)-te Zeile, \(i\in\IN\), in Gl. (22) identisch sind. Daher gibt es nur \(h\) verschiedene Gleichungen.

Von praktischem Interesse ist die Suche nach dem gültigen dualen Fenster \(\vb{u}_d\), das einem gegebenen Vektor \(\vb{d}\in\IC^M\) am nächsten liegt. Unter Verwendung eines \(h\)-dimensionalen Vektors \(\vb{\lambda}\) von Lagrange-Multiplikatoren erhalten wir das konvexe quadratische Programmierproblem:

\[\begin{split}\vb{u}_d = \min_{\vb{u}}{ \frac{1}{2}\lVert\vb{d} - \vb{u}\rVert^2 } \quad\text{w.r.t.}\quad \conjT{\vb{V}}\vb{u} = \vb{1} \qquad\Leftrightarrow\qquad \begin{bmatrix} \vb{I} & \vb{V}\\ \conjT{\vb{V}} & \vb{0} \end{bmatrix} \begin{bmatrix} \vb{u}_d \\ \vb{\lambda} \end{bmatrix} = \begin{bmatrix} \vb{d}\\ \vb{1} \end{bmatrix}\ .\end{split}\]

Eine geschlossene Formel kann durch symbolisches Invertieren der \(2\times2\)-Blockmatrix berechnet werden, was ergibt:

(25)\[\begin{split}\vb{u}_d &= \underbrace{\vb{V}\inv{\conjT{\vb{V}}\vb{V}}}_{% =:\vb{Q}\in\IC^{M\times h}} \vb{1} + \big(\vb{I} - \vb{Q}\conjT{\vb{V}}\big)\vb{d} = \vb{w}_d + \vb{d} - \vb{q}_d\ ,\\ \vb{w}_d &= \vb{Q}\vb{1}\ ,\qquad \vb{q}_d = \vb{Q}\conjT{\vb{V}}\vb{d}\ ,\\ Q[i,j] &= \frac{ w[i] \delta_{i-j, \eta h} }{% \sum_{k=0}^M |w[k]|^2\,\delta_{i-k, \xi h} } ,\qquad w_d[i] = \frac{w[i] }{ \sum_{l=0}^M \conj{w[l]} w[l] \delta_{i-l, \xi h} }\ ,\\ q_d[i] &= w[i] \frac{\sum_{j=1}^h \delta_{i-j, \eta h} \sum_{l=1}^M \conj{w[l]} d[l] \delta_{j-l, \xi h} }{% \sum_{l=0}^M \conj{w[l]} w[l] \delta_{i-l, \zeta h} } = w_d[i] \sum_{l=1}^M \conj{w[l]} d[l] \delta_{i-l, \eta h}\ ,\end{split}\]

mit \(\eta,\xi,\zeta\in\IZ\). Beachten Sie, dass der erste Term \(\vb{w}_d\) gleich der in Gl. (21) angegebenen Lösung ist und dass die Inverse von \(\conjT{\vb{V}}\vb{V}\) existieren muss, andernfalls ist die STFT nicht invertierbar. Wenn \(\vb{d}=\vb{0}\) ist, wird die Lösung \(\vb{w}_d\) erhalten. Daher minimiert \(\vb{w}_d\) die \(L^2\)-Norm \(\lVert\vb{u}\rVert\), was die Begründung für ihren Namen "kanonisches Dualfenster" ist. Manchmal ist es wünschenswerter, den Vektor zu finden, der der Richtung am nächsten liegt, und die Vektorlänge zu ignorieren. Dies kann durch Einführung eines Skalierungsfaktors \(\alpha\in\IC\) erreicht werden, um \(\lVert\alpha\vb{d} - \vb{u}\rVert^2\) zu minimieren. Da Gl. (25) bereits eine allgemeine Lösung liefert, können wir schreiben

\[\begin{split} \alpha_{\min} &= \min_{\alpha}{ \frac{1}{2}\big\lVert\alpha\vb{d} - \vb{u}_d(\alpha)\big\rVert^2 }\ ,\qquad \vb{u}_d(\alpha) = \vb{w}_d + \alpha\vb{d} - \alpha\vb{q}_d \qquad\Leftrightarrow\\ \alpha_{\min} &= \conjT{\vb{q}_d}\vb{w}_d \big/\, \conjT{\vb{q}_d}\vb{q}_d \ .\end{split}\]

Der Fall, in dem das Fenster \(w[m]\) und das Dualfenster \(u[m]\) gleich sind, kann leicht aus Gl. (23) abgeleitet werden, was zu \(h\) Bedingungen der Form

(26)\[\sum_{p=0}^{\lfloor M / h \rfloor} \big|w[m+ph]\big|^2 = 1\ , \qquad m \in \{0, \ldots, h-1\}\ .\]

Beachten Sie, dass jede Fenstersample \(w[m]\) nur einmal in den \(h\) Gleichungen vorkommt. Um ein nächstgelegenes Fenster \(\vb{w}\) für ein gegebenes Fenster \(\vb{d}\) zu finden, ist es unkompliziert: Teilen Sie \(\vb{d}\) gemäß Gl. (26) auf und normalisieren Sie die Länge jeder Partition auf Eins. In diesem Fall ist \(w[m]\) auch ein kanonisches Dualfenster, was man erkennen kann, indem man feststellt, dass das Setzen von \(u[m]=w[m]\) in Gl. (24) äquivalent dazu ist, dass der Nenner in Gl. (21) Eins ist.

Darüber hinaus ist, wenn Gl. (26) gilt, die Matrix \(\vb{D}\) aus Gl. (16) die Identitätsmatrix, wodurch die STFT \(\vb{G}\) eine unitäre Abbildung ist, d.h. \(\conjT{\vb{G}}\vb{G}=\vb{I}\). Beachten Sie, dass dies nur gilt, wenn eine unitäre DFT von Gl. (13) verwendet wird. Die Implementierung ShortTimeFFT verwendet die Standard-DFT von Gl. (6). Daher muss das Skalarprodukt im STFT-Raum dort mit \(1/M\) skaliert werden, um sicherzustellen, dass die Schlüsseleigenschaft unitärer Abbildungen, die Gleichheit der Skalarprodukte, gilt. D.h.

(27)\[\langle x, y\rangle = \sum_k x[k]\, \conj{y[k]} \stackrel{\stackrel{\text{unitary}}{\downarrow}}{=} \frac{1}{M}\sum_{q,p} S_x[q,p]\, \conj{S_y[q,p]}\ ,\]

wobei \(S_{x,y}\) die STFT von \(x,y\) ist. Alternativ kann das Fenster mit \(1/\sqrt{M}\) und das Dual mit \(\sqrt{M}\) skaliert werden, um eine unitäre Abbildung zu erhalten, die in from_win_equals_dual implementiert ist.

Vergleich mit der Legacy-Implementierung

Die Funktionen stft, istft und das spectrogram stammen aus der Zeit vor der Implementierung von ShortTimeFFT. Dieser Abschnitt erörtert die Hauptunterschiede zwischen den älteren "Legacy"- und den neueren ShortTimeFFT-Implementierungen. Die Hauptmotivation für eine Überarbeitung war die Erkenntnis, dass die Integration von Dualfenstern nicht auf sinnvolle Weise ohne Kompatibilitätsbruch erfolgen konnte. Dies eröffnete die Möglichkeit, die Code-Struktur und die Parametrisierung zu überdenken und damit einige implizite Verhaltensweisen expliziter zu machen.

Das folgende Beispiel vergleicht die beiden STFTs eines komplexwertigen Chrip-Signals mit negativer Steigung

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.fft import fftshift
>>> from scipy.signal import stft, istft, spectrogram, ShortTimeFFT
...
>>> fs, N = 200, 1001  # 200 Hz sampling rate for 5 s signal
>>> t_z = np.arange(N) / fs  # time indexes for signal
>>> z = np.exp(2j*np.pi*70 * (t_z - 0.2*t_z**2))  # complex-valued chirp
...
>>> nperseg, noverlap = 50, 40
>>> win = ('gaussian', 1e-2 * fs)  # Gaussian with 0.01 s standard dev.
...
>>> # Legacy STFT:
>>> f0_u, t0, Sz0_u = stft(z, fs, win, nperseg, noverlap,
...                        return_onesided=False, scaling='spectrum')
>>> f0, Sz0 = fftshift(f0_u), fftshift(Sz0_u, axes=0)
...
>>> # New STFT:
>>> SFT = ShortTimeFFT.from_window(win, fs, nperseg, noverlap, fft_mode='centered',
...                                scale_to='magnitude', phase_shift=None)
>>> Sz1 = SFT.stft(z)
...
>>> # Plot results:
>>> fig1, axx = plt.subplots(2, 1, sharex='all', sharey='all',
...                          figsize=(6., 5.))  # enlarge figure a bit
>>> t_lo, t_hi, f_lo, f_hi = SFT.extent(N, center_bins=True)
>>> axx[0].set_title(r"Legacy stft() produces $%d\times%d$ points" % Sz0.T.shape)
>>> axx[0].set_xlim(t_lo, t_hi)
>>> axx[0].set_ylim(f_lo, f_hi)
>>> axx[1].set_title(r"ShortTimeFFT produces $%d\times%d$ points" % Sz1.T.shape)
>>> axx[1].set_xlabel(rf"Time $t$ in seconds ($\Delta t= {SFT.delta_t:g}\,$s)")
...
>>> # Calculate extent of plot with centered bins since
>>> # imshow does not interpolate by default:
>>> dt2 = (nperseg-noverlap) / fs / 2  # equals SFT.delta_t / 2
>>> df2 = fs / nperseg / 2  # equals SFT.delta_f / 2
>>> extent0 = (-dt2, t0[-1] + dt2, f0[0] - df2, f0[-1] - df2)
>>> extent1 = SFT.extent(N, center_bins=True)
...
>>> kw = dict(origin='lower', aspect='auto', cmap='viridis')
>>> im1a = axx[0].imshow(abs(Sz0), extent=extent0, **kw)
>>> im1b = axx[1].imshow(abs(Sz1), extent=extent1, **kw)
>>> fig1.colorbar(im1b, ax=axx, label="Magnitude $|S_z(t, f)|$")
>>> _ = fig1.supylabel(r"Frequency $f$ in Hertz ($\Delta f = %g\,$Hz)" %
...                    SFT.delta_f, x=0.08, y=0.5, fontsize='medium')
>>> plt.show()

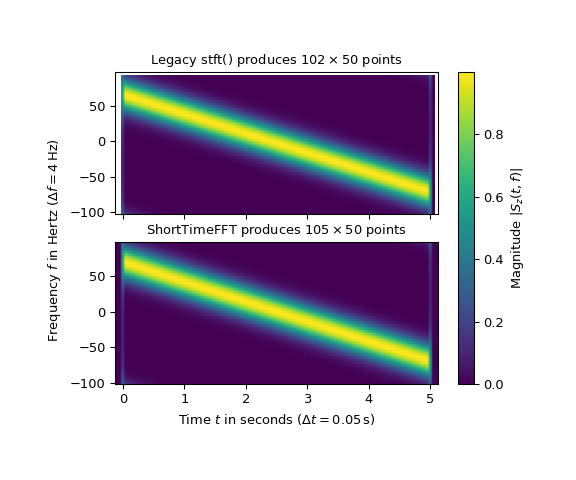
Dass die ShortTimeFFT 3 mehr Zeitschlitze erzeugt als die Legacy-Version, ist der Hauptunterschied. Wie im Abschnitt Sliding Windows dargelegt, werden alle Zeitschlitze, die das Signal berühren, in der neuen Version einbezogen. Dies hat den Vorteil, dass die STFT wie im Codebeispiel ShortTimeFFT gezeigt werden kann, zerlegt und wieder zusammengesetzt werden kann. Darüber hinaus macht die Verwendung aller berührenden Zeitschlitze die ISTFT robuster bei Fenstern, die irgendwo Null sind.

Beachten Sie, dass die Zeitschlitze mit identischen Zeitstempeln identische Ergebnisse liefern (bis auf numerische Genauigkeit), d.h.

>>> np.allclose(Sz0, Sz1[:, 2:-1])
True

Generell enthalten diese zusätzlichen Zeitschlitze nicht-Null-Werte. Aufgrund der großen Überlappung in unserem Beispiel sind sie recht klein. Z.B.

>>> abs(Sz1[:, 1]).min(), abs(Sz1[:, 1]).max()
(6.925060911593139e-07, 8.00271269218721e-07)

Die ISTFT kann verwendet werden, um das ursprüngliche Signal zu rekonstruieren

>>> t0_r, z0_r = istft(Sz0_u, fs, win, nperseg, noverlap,
...                    input_onesided=False, scaling='spectrum')
>>> z1_r = SFT.istft(Sz1, k1=N)
...
>>> len(z0_r), len(z)
(1010, 1001)
>>> np.allclose(z0_r[:N], z)
True
>>> np.allclose(z1_r, z)
True

Beachten Sie, dass die Legacy-Implementierung ein Signal zurückgibt, das länger als das Original ist. Auf der anderen Seite ermöglicht die neue istft die explizite Angabe des Start- und Endindexes k0 bzw. k1 des rekonstruierten Signals. Die Längenabweichung in der alten Implementierung wird dadurch verursacht, dass die Signallänge kein Vielfaches der Zeitschlitze ist.

Weitere Unterschiede zwischen der neuen und der Legacy-Version in diesem Beispiel sind

• Der Parameter fft_mode='centered' stellt sicher, dass die Nullfrequenz bei zweiseitigen FFTs in der Darstellung vertikal zentriert ist. Bei der Legacy-Implementierung muss fftshift verwendet werden. fft_mode='twosided' erzeugt das gleiche Verhalten wie die alte Version.

• Der Parameter phase_shift=None stellt identische Phasen der beiden Versionen sicher. Der Standardwert von 0 in ShortTimeFFT erzeugt STFT-Zeitschlitze mit einem zusätzlichen linearen Phasenterm.

Ein Spektrogramm ist definiert als das absolute Quadrat der STFT [9]. Das von ShortTimeFFT bereitgestellte spectrogram hält sich an diese Definition, d.h.

>>> np.allclose(SFT.spectrogram(z), abs(Sz1)**2)
True

Auf der anderen Seite liefert das Legacy- spectrogram eine andere STFT-Implementierung, wobei der Hauptunterschied in der anderen Handhabung der Signalränder liegt. Das folgende Beispiel zeigt, wie ShortTimeFFT verwendet werden kann, um eine identische SFT zu erhalten, wie sie mit dem Legacy- spectrogram erzeugt wird.

>>> # Legacy spectrogram (detrending for complex signals not useful):
>>> f2_u, t2, Sz2_u = spectrogram(z, fs, win, nperseg, noverlap,
...                               detrend=None, return_onesided=False,
...                               scaling='spectrum', mode='complex')
>>> f2, Sz2 = fftshift(f2_u), fftshift(Sz2_u, axes=0)
...
>>> # New STFT:
... SFT = ShortTimeFFT.from_window(win, fs, nperseg, noverlap,
...                                fft_mode='centered',
...                                scale_to='magnitude', phase_shift=None)
>>> Sz3 = SFT.stft(z, p0=0, p1=(N-noverlap)//SFT.hop, k_offset=nperseg//2)
>>> t3 = SFT.t(N, p0=0, p1=(N-noverlap)//SFT.hop, k_offset=nperseg//2)
...
>>> np.allclose(t2, t3)
True
>>> np.allclose(f2, SFT.f)
True
>>> np.allclose(Sz2, Sz3)
True

Der Unterschied zu den anderen STFTs besteht darin, dass die Zeitschlitze nicht bei 0 beginnen, sondern bei nperseg//2, d.h.

>>> t2
array([0.125, 0.175, 0.225, 0.275, 0.325, 0.375, 0.425, 0.475, 0.525,
       ...
       4.625, 4.675, 4.725, 4.775, 4.825, 4.875])

Darüber hinaus werden nur Zeitschlitze zurückgegeben, die nicht nach rechts überlappen, wobei der letzte Zeitschlitz bei 4,875 s zentriert ist, was ihn kürzer macht als bei der Standardparametrisierung von stft.

Unter Verwendung des Parameters mode kann das Legacy- spectrogram auch 'angle', 'phase', 'psd' oder 'magnitude' zurückgeben. Das scaling-Verhalten des Legacy- spectrogram ist nicht eindeutig, da es von den Parametern mode, scaling und return_onesided abhängt. Es gibt keine direkte Entsprechung für alle Kombinationen in ShortTimeFFT, da es nur 'magnitude', 'psd' oder gar kein scaling des Fensters bietet. Die folgende Tabelle zeigt diese Entsprechungen

Legacy spectrogram				ShortTimeFFT
mode	scaling	return_onesided		fft_mode	scaling
psd	density	True		onesided2X	psd
psd	density	False		twosided	psd
magnitude	spectrum	True		onesided	magnitude
magnitude	spectrum	False		twosided	magnitude
complex	spectrum	True		onesided	magnitude
complex	spectrum	False		twosided	magnitude
psd	spectrum	True		—	—
psd	spectrum	False		—	—
complex	density	True		—	—
complex	density	False		—	—
magnitude	density	True		—	—
magnitude	density	False		—	—
—	—	—		*	None

Bei Verwendung von onesided-Ausgabe bei komplexwertigen Eingangssignalen schaltet das alte spectrogram in den two-sided-Modus. Die ShortTimeFFT löst einen TypeError aus, da die verwendete Funktion rfft nur reellwertige Eingaben akzeptiert. Konsultieren Sie den Abschnitt Spektralanalyse oben für eine Diskussion über die verschiedenen Spektraldarstellungen, die sich aus den verschiedenen Parametrisierungen ergeben.

Referenzen

Weiterführende Lektüre und verwandte Software

[1]

„Fourier-Transformation“, Wikipedia, https://en.wikipedia.org/wiki/Fourier_transform

[2]

„Spektraldichte“, Wikipedia, https://en.wikipedia.org/wiki/Spectral_density

[3]

„Diskrete Fourier-Transformation“, Wikipedia, https://en.wikipedia.org/wiki/Discrete_Fourier_transform

[4]

„Spektral-Leckage“, Wikipedia, https://en.wikipedia.org/wiki/Spectral_leakage

[5]

„Nyquist-Shannon-Abtasttheorem“, Wikipedia, https://en.wikipedia.org/wiki/Nyquist-Shannon_sampling_theorem

[6]

N.R. Lomb „Least-squares frequency analysis of unequally spaced data“, Astrophysics and Space Science, Bd. 39, S. 447-462, 1976

[7]

J.D. Scargle „Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data“, The Astrophysical Journal, Bd. 263, S. 835-853, 1982

[8]

M. Zechmeister und M. Kürster, „The generalised Lomb-Scargle periodogram. A new formalism for the floating-mean and Keplerian periodograms,“ Astronomy and Astrophysics, Bd. 496, S. 577-584, 2009

[9] (1,2,3,4)

Karlheinz Gröchenig: „Foundations of Time-Frequency Analysis“, Birkhäuser Boston 2001, DOI:10.1007/978-1-4612-0003-1

[10] (1,2,3)

Ole Christensen: „An Introduction to Frames and Riesz Bases“, Birkhäuser Boston 2016, DOI:10.1007/978-3-319-25613-9