Lineare Algebra (scipy.linalg)#
Wenn SciPy mit den optimierten ATLAS LAPACK- und BLAS-Bibliotheken erstellt wird, verfügt es über sehr schnelle Fähigkeiten für die lineare Algebra. Wenn Sie tief genug graben, sind alle rohen LAPACK- und BLAS-Bibliotheken für Sie verfügbar, um noch mehr Geschwindigkeit zu erzielen. In diesem Abschnitt werden einige einfacher zu bedienende Schnittstellen zu diesen Routinen beschrieben.
Alle diese Routinen für lineare Algebra erwarten ein Objekt, das in ein 2D-Array konvertiert werden kann. Die Ausgabe dieser Routinen ist ebenfalls ein 2D-Array.
scipy.linalg vs numpy.linalg#
scipy.linalg enthält alle Funktionen in numpy.linalg. plus einige andere fortschrittlichere, die nicht in numpy.linalg enthalten sind.
Ein weiterer Vorteil der Verwendung von scipy.linalg gegenüber numpy.linalg ist, dass es immer mit BLAS/LAPACK-Unterstützung kompiliert wird, während dies für NumPy optional ist. Daher kann die SciPy-Version schneller sein, je nachdem, wie NumPy installiert wurde.
Daher sollten Sie, es sei denn, Sie möchten scipy nicht als Abhängigkeit zu Ihrem numpy-Programm hinzufügen, scipy.linalg anstelle von numpy.linalg verwenden.
numpy.matrix vs 2D numpy.ndarray#
Die Klassen, die Matrizen und grundlegende Operationen wie Matrixmultiplikation und Transponierung darstellen, sind Teil von numpy. Der Einfachheit halber fassen wir hier die Unterschiede zwischen numpy.matrix und numpy.ndarray zusammen.
numpy.matrix ist eine Matrixklasse mit einer komfortableren Schnittstelle als numpy.ndarray für Matrixoperationen. Diese Klasse unterstützt beispielsweise die MATLAB-ähnliche Erstellungssyntax über das Semikolon, hat die Matrixmultiplikation als Standard für den Operator * und enthält die Mitglieder I und T, die als Abkürzungen für Inverse und Transponierte dienen.
>>> import numpy as np
>>> A = np.asmatrix('[1 2;3 4]')
>>> A
matrix([[1, 2],
[3, 4]])
>>> A.I
matrix([[-2. , 1. ],
[ 1.5, -0.5]])
>>> b = np.asmatrix('[5 6]')
>>> b
matrix([[5, 6]])
>>> b.T
matrix([[5],
[6]])
>>> A*b.T
matrix([[17],
[39]])
Trotz ihres Komforts wird die Verwendung der Klasse numpy.matrix nicht empfohlen, da sie nichts hinzufügt, was nicht mit 2D- numpy.ndarray-Objekten erreicht werden kann, und zu Verwirrung darüber führen kann, welche Klasse verwendet wird. Zum Beispiel kann der obige Code umgeschrieben werden als
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
[3, 4]])
>>> linalg.inv(A)
array([[-2. , 1. ],
[ 1.5, -0.5]])
>>> b = np.array([[5,6]]) #2D array
>>> b
array([[5, 6]])
>>> b.T
array([[5],
[6]])
>>> A*b #not matrix multiplication!
array([[ 5, 12],
[15, 24]])
>>> A.dot(b.T) #matrix multiplication
array([[17],
[39]])
>>> b = np.array([5,6]) #1D array
>>> b
array([5, 6])
>>> b.T #not matrix transpose!
array([5, 6])
>>> A.dot(b) #does not matter for multiplication
array([17, 39])
scipy.linalg-Operationen können gleichermaßen auf numpy.matrix oder 2D- numpy.ndarray-Objekte angewendet werden.
Grundlegende Routinen#
Finden der Inversen#
Die Inverse einer Matrix \(\mathbf{A}\) ist die Matrix \(\mathbf{B}\), so dass \(\mathbf{AB}=\mathbf{I}\), wobei \(\mathbf{I}\) die Einheitsmatrix ist, die Einsen auf der Hauptdiagonale enthält. Normalerweise wird \(\mathbf{B}\) als \(\mathbf{B}=\mathbf{A}^{-1}\) bezeichnet. In SciPy erhalten Sie die Matrixinverse des NumPy-Arrays A mit linalg.inv (A) oder mit A.I, wenn A eine Matrix ist. Zum Beispiel sei
dann
Das folgende Beispiel demonstriert diese Berechnung in SciPy
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,3,5],[2,5,1],[2,3,8]])
>>> A
array([[1, 3, 5],
[2, 5, 1],
[2, 3, 8]])
>>> linalg.inv(A)
array([[-1.48, 0.36, 0.88],
[ 0.56, 0.08, -0.36],
[ 0.16, -0.12, 0.04]])
>>> A.dot(linalg.inv(A)) #double check
array([[ 1.00000000e+00, -1.11022302e-16, -5.55111512e-17],
[ 3.05311332e-16, 1.00000000e+00, 1.87350135e-16],
[ 2.22044605e-16, -1.11022302e-16, 1.00000000e+00]])
Lösen eines linearen Systems#
Das Lösen von linearen Gleichungssystemen ist mit dem SciPy-Befehl linalg.solve unkompliziert. Dieser Befehl erwartet eine Eingabematrix und einen Vektor auf der rechten Seite. Der Lösungsvektor wird dann berechnet. Es wird eine Option für die Eingabe einer symmetrischen Matrix angeboten, die die Verarbeitung beschleunigen kann, wenn sie anwendbar ist. Angenommen, es soll das folgende simultane Gleichungssystem gelöst werden
Wir könnten den Lösungsvektor durch eine Matrixinverse finden
Es ist jedoch besser, den Befehl linalg.solve zu verwenden, der schneller und numerisch stabiler sein kann. In diesem Fall liefert er jedoch das gleiche Ergebnis wie im folgenden Beispiel gezeigt.
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> A
array([[1, 2],
[3, 4]])
>>> b = np.array([[5], [6]])
>>> b
array([[5],
[6]])
>>> linalg.inv(A).dot(b) # slow
array([[-4. ],
[ 4.5]])
>>> A.dot(linalg.inv(A).dot(b)) - b # check
array([[ 8.88178420e-16],
[ 2.66453526e-15]])
>>> np.linalg.solve(A, b) # fast
array([[-4. ],
[ 4.5]])
>>> A.dot(np.linalg.solve(A, b)) - b # check
array([[ 0.],
[ 0.]])
Finden der Determinante#
Die Determinante einer quadratischen Matrix \(\mathbf{A}\) wird oft als \(\left|\mathbf{A}\right|\) bezeichnet und ist eine Größe, die in der linearen Algebra häufig verwendet wird. Angenommen, \(a_{ij}\) sind die Elemente der Matrix \(\mathbf{A}\) und \(M_{ij}=\left|\mathbf{A}_{ij}\right|\) ist die Determinante der Matrix, die durch Entfernen der \(i^{\textrm{th}}\)-ten Zeile und \(j^{\textrm{th}}\)-ten Spalte von \(\mathbf{A}\) übrig bleibt. Dann gilt für jede Zeile \(i,\)
Dies ist eine rekursive Methode zur Definition der Determinante, wobei der Basisfall durch die Annahme definiert ist, dass die Determinante einer \(1\times1\)-Matrix das einzige Matrixelement ist. In SciPy kann die Determinante mit linalg.det berechnet werden. Zum Beispiel ist die Determinante von
ist
In SciPy wird dies wie in diesem Beispiel gezeigt berechnet
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2],[3,4]])
>>> A
array([[1, 2],
[3, 4]])
>>> linalg.det(A)
-2.0
Normen berechnen#
Matrix- und Vektornormen können ebenfalls mit SciPy berechnet werden. Eine breite Palette von Normdefinitionen ist über verschiedene Parameter für das Argument `order` von linalg.norm verfügbar. Diese Funktion nimmt ein Array vom Rang 1 (Vektoren) oder Rang 2 (Matrizen) und ein optionales `order`-Argument (Standard ist 2) entgegen. Basierend auf diesen Eingaben wird eine Vektor- oder Matrixnorm der angeforderten Ordnung berechnet.
Für einen Vektor *x* kann der Parameter `order` jede reelle Zahl sein, einschließlich inf oder -inf. Die berechnete Norm ist
Für eine Matrix \(\mathbf{A}\) sind die einzigen gültigen Werte für die Norm \(\pm2,\pm1,\) \(\pm\) inf und 'fro' (oder 'f'). Daher gilt:
wobei \(\sigma_{i}\) die singulären Werte von \(\mathbf{A}\) sind.
Beispiele
>>> import numpy as np
>>> from scipy import linalg
>>> A=np.array([[1, 2], [3, 4]])
>>> A
array([[1, 2],
[3, 4]])
>>> linalg.norm(A)
5.4772255750516612
>>> linalg.norm(A, 'fro') # frobenius norm is the default
5.4772255750516612
>>> linalg.norm(A, 1) # L1 norm (max column sum)
6.0
>>> linalg.norm(A, -1)
4.0
>>> linalg.norm(A, np.inf) # L inf norm (max row sum)
7.0
Lösen von linearen Kleinstquadratproblemen und Pseudoinversen#
Lineare Kleinstquadratprobleme treten in vielen Bereichen der angewandten Mathematik auf. Bei diesem Problem wird nach einem Satz linearer Skalierungskoeffizienten gesucht, die es einem Modell ermöglichen, die Daten anzupassen. Insbesondere wird angenommen, dass die Daten \(y_{i}\) mit den Daten \(\mathbf{x}_{i}\) über einen Satz von Koeffizienten \(c_{j}\) und Modellfunktionen \(f_{j}\left(\mathbf{x}_{i}\right)\) über das Modell verbunden sind
wobei \(\epsilon_{i}\) die Unsicherheit in den Daten darstellt. Die Kleinstquadratstrategie besteht darin, die Koeffizienten \(c_{j}\) so zu wählen, dass
minimiert wird. Theoretisch tritt ein globales Minimum auf, wenn
oder
wo
Wenn \(\mathbf{A^{H}A}\) invertierbar ist, dann
wobei \(\mathbf{A}^{\dagger}\) die Pseudoinverse von \(\mathbf{A}.\) Beachten Sie, dass das Modell mit dieser Definition von \(\mathbf{A}\) geschrieben werden kann als
Der Befehl linalg.lstsq löst das lineare Kleinstquadratproblem für \(\mathbf{c}\) gegeben \(\mathbf{A}\) und \(\mathbf{y}\). Zusätzlich findet linalg.pinv \(\mathbf{A}^{\dagger}\) gegeben \(\mathbf{A}.\)
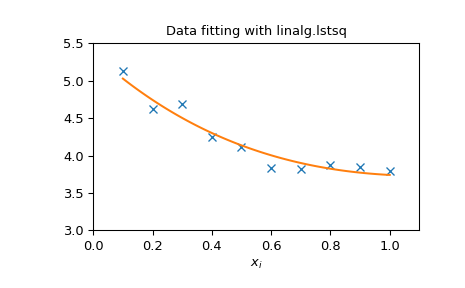
Das folgende Beispiel und die Abbildung demonstrieren die Verwendung von linalg.lstsq und linalg.pinv zum Lösen eines Datenanpassungsproblems. Die unten gezeigten Daten wurden mit dem Modell generiert
wobei \(x_{i}=0.1i\) für \(i=1\ldots10\), \(c_{1}=5\) und \(c_{2}=4.\) Rauschen wird zu \(y_{i}\) hinzugefügt und die Koeffizienten \(c_{1}\) und \(c_{2}\) werden mithilfe von linearen Kleinstquadraten geschätzt.
>>> import numpy as np
>>> from scipy import linalg
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> c1, c2 = 5.0, 2.0
>>> i = np.r_[1:11]
>>> xi = 0.1*i
>>> yi = c1*np.exp(-xi) + c2*xi
>>> zi = yi + 0.05 * np.max(yi) * rng.standard_normal(len(yi))
>>> A = np.c_[np.exp(-xi)[:, np.newaxis], xi[:, np.newaxis]]
>>> c, resid, rank, sigma = linalg.lstsq(A, zi)
>>> xi2 = np.r_[0.1:1.0:100j]
>>> yi2 = c[0]*np.exp(-xi2) + c[1]*xi2
>>> plt.plot(xi,zi,'x',xi2,yi2)
>>> plt.axis([0,1.1,3.0,5.5])
>>> plt.xlabel('$x_i$')
>>> plt.title('Data fitting with linalg.lstsq')
>>> plt.show()
Generalisierte Inverse#
Die verallgemeinerte Inverse wird mit dem Befehl linalg.pinv berechnet. Sei \(\mathbf{A}\) eine \(M\times N\)-Matrix, dann gilt für \(M>N\) die verallgemeinerte Inverse
während für eine \(M<N\)-Matrix die verallgemeinerte Inverse
Wenn \(M=N\), dann gilt
sofern \(\mathbf{A}\) invertierbar ist.
Zerlegungen#
In vielen Anwendungen ist es nützlich, eine Matrix mithilfe anderer Darstellungen zu zerlegen. SciPy unterstützt mehrere Zerlegungen.
Eigenwerte und Eigenvektoren#
Das Eigenwert-Eigenvektor-Problem ist eine der am häufigsten verwendeten Operationen der linearen Algebra. In einer populären Form besteht das Eigenwert-Eigenvektor-Problem darin, für eine quadratische Matrix \(\mathbf{A}\) Skalare \(\lambda\) und entsprechende Vektoren \(\mathbf{v}\) zu finden, so dass
Für eine \(N\times N\)-Matrix gibt es \(N\) (nicht notwendigerweise verschiedene) Eigenwerte — Wurzeln des (charakteristischen) Polynoms
Die Eigenvektoren, \(\mathbf{v}\), werden manchmal auch als rechte Eigenvektoren bezeichnet, um sie von einer anderen Menge linker Eigenvektoren zu unterscheiden, die erfüllen
oder
Mit seinen Standard-Optionalparametern gibt der Befehl linalg.eig \(\lambda\) und \(\mathbf{v}.\) Er kann jedoch auch \(\mathbf{v}_{L}\) und nur \(\lambda\) selbst zurückgeben ( linalg.eigvals gibt ebenfalls nur \(\lambda\) zurück).
Zusätzlich kann linalg.eig auch das allgemeinere Eigenwertproblem lösen
für quadratische Matrizen \(\mathbf{A}\) und \(\mathbf{B}.\) Das Standard-Eigenwertproblem ist ein Beispiel für das allgemeine Eigenwertproblem für \(\mathbf{B}=\mathbf{I}.\) Wenn ein verallgemeinertes Eigenwertproblem gelöst werden kann, liefert es eine Zerlegung von \(\mathbf{A}\) als
wobei \(\mathbf{V}\) die Sammlung von Eigenvektoren in Spalten und \(\boldsymbol{\Lambda}\) eine Diagonalmatrix von Eigenwerten ist.
Per Definition sind Eigenvektoren nur bis auf einen konstanten Skalierungsfaktor definiert. In SciPy wird der Skalierungsfaktor für die Eigenvektoren so gewählt, dass \(\left\Vert \mathbf{v}\right\Vert ^{2}=\sum_{i}v_{i}^{2}=1.\)
Betrachten wir als Beispiel die Eigenwerte und Eigenvektoren der Matrix
Das charakteristische Polynom ist
Die Wurzeln dieses Polynoms sind die Eigenwerte von \(\mathbf{A}\)
Die Eigenvektoren, die zu jedem Eigenwert gehören, können mithilfe der ursprünglichen Gleichung gefunden werden. Die Eigenvektoren, die zu diesen Eigenwerten gehören, können dann gefunden werden.
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1, 2], [3, 4]])
>>> la, v = linalg.eig(A)
>>> l1, l2 = la
>>> print(l1, l2) # eigenvalues
(-0.3722813232690143+0j) (5.372281323269014+0j)
>>> print(v[:, 0]) # first eigenvector
[-0.82456484 0.56576746]
>>> print(v[:, 1]) # second eigenvector
[-0.41597356 -0.90937671]
>>> print(np.sum(abs(v**2), axis=0)) # eigenvectors are unitary
[1. 1.]
>>> v1 = np.array(v[:, 0]).T
>>> print(linalg.norm(A.dot(v1) - l1*v1)) # check the computation
3.23682852457e-16
Singulärwertzerlegung#
Die Singulärwertzerlegung (SVD) kann als Erweiterung des Eigenwertproblems auf Matrizen betrachtet werden, die nicht quadratisch sind. Sei \(\mathbf{A}\) eine \(M\times N\)-Matrix mit beliebigen \(M\) und \(N\). Die Matrizen \(\mathbf{A}^{H}\mathbf{A}\) und \(\mathbf{A}\mathbf{A}^{H}\) sind quadratische hermitesche Matrizen [1] der Größe \(N\times N\) bzw. \(M\times M\). Es ist bekannt, dass die Eigenwerte von quadratischen hermiteschen Matrizen reell und nicht negativ sind. Darüber hinaus gibt es höchstens \(\min\left(M,N\right)\) identische von Null verschiedene Eigenwerte von \(\mathbf{A}^{H}\mathbf{A}\) und \(\mathbf{A}\mathbf{A}^{H}.\) Definiere diese positiven Eigenwerte als \(\sigma_{i}^{2}.\) Die Quadratwurzeln davon werden als Singulärwerte von \(\mathbf{A}\) bezeichnet. Die Eigenvektoren von \(\mathbf{A}^{H}\mathbf{A}\) werden spaltenweise in einer \(N\times N\)-unitären [2]-Matrix \(\mathbf{V}\) gesammelt, während die Eigenvektoren von \(\mathbf{A}\mathbf{A}^{H}\) spaltenweise in der unitären Matrix \(\mathbf{U}\) gesammelt werden. Die Singulärwerte werden in einer \(M\times N\)-Nullmatrix \(\mathbf{\boldsymbol{\Sigma}}\) gesammelt, deren Hauptdiagonaleinträge auf die Singulärwerte gesetzt sind. Dann gilt
ist die Singulärwertzerlegung von \(\mathbf{A}.\) Jede Matrix hat eine Singulärwertzerlegung. Manchmal werden die Singulärwerte als Spektrum von \(\mathbf{A}\) bezeichnet. Der Befehl linalg.svd gibt \(\mathbf{U}\), \(\mathbf{V}^{H}\) und \(\sigma_{i}\) als Array der Singulärwerte zurück. Um die Matrix \(\boldsymbol{\Sigma}\) zu erhalten, verwenden Sie linalg.diagsvd. Das folgende Beispiel veranschaulicht die Verwendung von linalg.svd
>>> import numpy as np
>>> from scipy import linalg
>>> A = np.array([[1,2,3],[4,5,6]])
>>> A
array([[1, 2, 3],
[4, 5, 6]])
>>> M,N = A.shape
>>> U,s,Vh = linalg.svd(A)
>>> Sig = linalg.diagsvd(s,M,N)
>>> U, Vh = U, Vh
>>> U
array([[-0.3863177 , -0.92236578],
[-0.92236578, 0.3863177 ]])
>>> Sig
array([[ 9.508032 , 0. , 0. ],
[ 0. , 0.77286964, 0. ]])
>>> Vh
array([[-0.42866713, -0.56630692, -0.7039467 ],
[ 0.80596391, 0.11238241, -0.58119908],
[ 0.40824829, -0.81649658, 0.40824829]])
>>> U.dot(Sig.dot(Vh)) #check computation
array([[ 1., 2., 3.],
[ 4., 5., 6.]])
LU-Zerlegung#
Die LU-Zerlegung findet eine Darstellung für die \(M\times N\)-Matrix \(\mathbf{A}\) als
wobei \(\mathbf{P}\) eine \(M\times M\)-Permutationsmatrix ist (eine Permutation der Zeilen der Einheitsmatrix), \(\mathbf{L}\) eine \(M\times K\)-untere Dreiecks- oder Trapezmatrix ist ( \(K=\min\left(M,N\right)\)) mit Einheitsdiagonale und \(\mathbf{U}\) eine obere Dreiecks- oder Trapezmatrix ist. Der SciPy-Befehl für diese Zerlegung ist linalg.lu.
Eine solche Zerlegung ist oft nützlich, um viele simultane Gleichungen zu lösen, bei denen die linke Seite nicht wechselt, die rechte Seite jedoch schon. Angenommen, wir werden lösen
für viele verschiedene \(\mathbf{b}_{i}\). Die LU-Zerlegung ermöglicht es, dies zu schreiben als
Da \(\mathbf{L}\) untere Dreiecksform hat, kann die Gleichung für \(\mathbf{U}\mathbf{x}_{i}\) und schließlich \(\mathbf{x}_{i}\) sehr schnell mithilfe von Vorwärts- und Rückwärtseinsetzung gelöst werden. Eine anfängliche Zeit für die Faktorisierung von \(\mathbf{A}\) ermöglicht eine sehr schnelle Lösung ähnlicher Gleichungssysteme in der Zukunft. Wenn die Absicht bei der Durchführung der LU-Zerlegung das Lösen linearer Systeme ist, dann sollte der Befehl linalg.lu_factor gefolgt von wiederholten Anwendungen des Befehls linalg.lu_solve verwendet werden, um das System für jede neue rechte Seite zu lösen.
Cholesky-Zerlegung#
Die Cholesky-Zerlegung ist ein Sonderfall der LU-Zerlegung, die auf hermitesche positiv definite Matrizen anwendbar ist. Wenn \(\mathbf{A}=\mathbf{A}^{H}\) und \(\mathbf{x}^{H}\mathbf{Ax}\geq0\) für alle \(\mathbf{x}\), dann können Zerlegungen von \(\mathbf{A}\) gefunden werden, so dass
wobei \(\mathbf{L}\) eine untere Dreiecksmatrix und \(\mathbf{U}\) eine obere Dreiecksmatrix ist. Beachten Sie, dass \(\mathbf{L}=\mathbf{U}^{H}.\) Der Befehl linalg.cholesky berechnet die Cholesky-Faktorisierung. Für die Verwendung der Cholesky-Faktorisierung zum Lösen von Gleichungssystemen gibt es auch die Routinen linalg.cho_factor und linalg.cho_solve, die ähnlich wie ihre LU-Zerlegungs-Gegenstücke funktionieren.
QR-Zerlegung#
Die QR-Zerlegung (manchmal auch als Polare Zerlegung bezeichnet) funktioniert für jedes \(M\times N\)-Array und findet eine \(M\times M\)-unitäre Matrix \(\mathbf{Q}\) und eine \(M\times N\)-obere Trapezmatrix \(\mathbf{R}\), so dass
Beachten Sie, dass, wenn die SVD von \(\mathbf{A}\) bekannt ist, die QR-Zerlegung gefunden werden kann.
impliziert, dass \(\mathbf{Q}=\mathbf{U}\) und \(\mathbf{R}=\boldsymbol{\Sigma}\mathbf{V}^{H}.\) Beachten Sie jedoch, dass in SciPy unabhängige Algorithmen zur Ermittlung von QR- und SVD-Zerlegungen verwendet werden. Der Befehl für die QR-Zerlegung ist linalg.qr.
Schur-Zerlegung#
Für eine quadratische \(N\times N\)-Matrix \(\mathbf{A}\) findet die Schur-Zerlegung (nicht notwendigerweise eindeutige) Matrizen \(\mathbf{T}\) und \(\mathbf{Z}\), so dass
wobei \(\mathbf{Z}\) eine unitäre Matrix und \(\mathbf{T}\) entweder eine obere Dreiecksmatrix oder eine quasi-obere Dreiecksmatrix ist, je nachdem, ob eine reelle oder komplexe Schur-Form angefordert wird. Für eine reelle Schur-Form sind sowohl \(\mathbf{T}\) als auch \(\mathbf{Z}\) reellwertig, wenn \(\mathbf{A}\) reellwertig ist. Wenn \(\mathbf{A}\) eine reellwertige Matrix ist, ist die reelle Schur-Form nur quasi-obere Dreiecksform, da \(2\times2\)-Blöcke aus der Hauptdiagonale hervorgehen, die zu komplexwertigen Eigenwerten gehören. Der Befehl linalg.schur findet die Schur-Zerlegung, während der Befehl linalg.rsf2csf \(\mathbf{T}\) und \(\mathbf{Z}\) von einer reellen Schur-Form in eine komplexe Schur-Form konvertiert. Die Schur-Form ist besonders nützlich bei der Berechnung von Matrixfunktionen.
Das folgende Beispiel veranschaulicht die Schur-Zerlegung
>>> from scipy import linalg
>>> A = np.asmatrix('[1 3 2; 1 4 5; 2 3 6]')
>>> T, Z = linalg.schur(A)
>>> T1, Z1 = linalg.schur(A, 'complex')
>>> T2, Z2 = linalg.rsf2csf(T, Z)
>>> T
array([[ 9.90012467, 1.78947961, -0.65498528],
[ 0. , 0.54993766, -1.57754789],
[ 0. , 0.51260928, 0.54993766]])
>>> T2
array([[ 9.90012467+0.00000000e+00j, -0.32436598+1.55463542e+00j,
-0.88619748+5.69027615e-01j],
[ 0. +0.00000000e+00j, 0.54993766+8.99258408e-01j,
1.06493862+3.05311332e-16j],
[ 0. +0.00000000e+00j, 0. +0.00000000e+00j,
0.54993766-8.99258408e-01j]])
>>> abs(T1 - T2) # different
array([[ 1.06604538e-14, 2.06969555e+00, 1.69375747e+00], # may vary
[ 0.00000000e+00, 1.33688556e-15, 4.74146496e-01],
[ 0.00000000e+00, 0.00000000e+00, 1.13220977e-15]])
>>> abs(Z1 - Z2) # different
array([[ 0.06833781, 0.88091091, 0.79568503], # may vary
[ 0.11857169, 0.44491892, 0.99594171],
[ 0.12624999, 0.60264117, 0.77257633]])
>>> T, Z, T1, Z1, T2, Z2 = map(np.asmatrix,(T,Z,T1,Z1,T2,Z2))
>>> abs(A - Z*T*Z.H) # same
matrix([[ 5.55111512e-16, 1.77635684e-15, 2.22044605e-15],
[ 0.00000000e+00, 3.99680289e-15, 8.88178420e-16],
[ 1.11022302e-15, 4.44089210e-16, 3.55271368e-15]])
>>> abs(A - Z1*T1*Z1.H) # same
matrix([[ 4.26993904e-15, 6.21793362e-15, 8.00007092e-15],
[ 5.77945386e-15, 6.21798014e-15, 1.06653681e-14],
[ 7.16681444e-15, 8.90271058e-15, 1.77635764e-14]])
>>> abs(A - Z2*T2*Z2.H) # same
matrix([[ 6.02594127e-16, 1.77648931e-15, 2.22506907e-15],
[ 2.46275555e-16, 3.99684548e-15, 8.91642616e-16],
[ 8.88225111e-16, 8.88312432e-16, 4.44104848e-15]])
Interpolationszerlegung#
scipy.linalg.interpolative enthält Routinen zur Berechnung der Interpolationszerlegung (ID) einer Matrix. Für eine Matrix \(A \in \mathbb{C}^{m \times n}\) vom Rang \(k \leq \min \{ m, n \}\) ist dies eine Faktorisierung
wobei \(\Pi = [\Pi_{1}, \Pi_{2}]\) eine Permutationsmatrix ist mit \(\Pi_{1} \in \{ 0, 1 \}^{n \times k}\), d.h. \(A \Pi_{2} = A \Pi_{1} T\). Dies kann äquivalent als \(A = BP\) geschrieben werden, wobei \(B = A \Pi_{1}\) und \(P = [I, T] \Pi^{\mathsf{T}}\) die Skelett- und Interpolationsmatrizen sind, beziehungsweise.
Siehe auch
scipy.linalg.interpolative — für weitere Informationen.
Matrixfunktionen#
Betrachten Sie die Funktion \(f\left(x\right)\) mit der Taylorreihenentwicklung
Eine Matrixfunktion kann mit dieser Taylorreihe für die quadratische Matrix \(\mathbf{A}\) wie folgt definiert werden:
Hinweis
Obwohl dies eine nützliche Darstellung einer Matrixfunktion darstellt, ist es selten die beste Methode zur Berechnung einer Matrixfunktion. Insbesondere wenn die Matrix nicht diagonalisierbar ist, können die Ergebnisse ungenau sein.
Exponential- und Logarithmusfunktionen#
Die Matrixexponentialfunktion ist eine der gebräuchlichsten Matrixfunktionen. Die bevorzugte Methode zur Implementierung der Matrixexponentialfunktion ist die Verwendung von Skalierung und einer Padé-Approximation für \(e^{x}\). Dieser Algorithmus ist als linalg.expm implementiert.
Die Umkehrung der Matrixexponentialfunktion ist der Matrixlogarithmus, der als Umkehrung der Matrixexponentialfunktion definiert ist
Der Matrixlogarithmus kann mit linalg.logm ermittelt werden.
Trigonometrische Funktionen#
Die trigonometrischen Funktionen \(\sin\), \(\cos\) und \(\tan\) sind für Matrizen in linalg.sinm, linalg.cosm bzw. linalg.tanm implementiert. Der Matrix-Sinus und -Cosinus können mit der Eulerschen Identität wie folgt definiert werden:
Der Tangens ist
und so ist der Matrix-Tangens definiert als
Hyperbolische trigonometrische Funktionen#
Die hyperbolischen trigonometrischen Funktionen \(\sinh\), \(\cosh\) und \(\tanh\) können ebenfalls für Matrizen mit den bekannten Definitionen definiert werden:
Diese Matrixfunktionen können über linalg.sinhm, linalg.coshm und linalg.tanhm gefunden werden.
Beliebige Funktion#
Schließlich kann jede beliebige Funktion, die eine komplexe Zahl entgegennimmt und eine komplexe Zahl zurückgibt, als Matrixfunktion über den Befehl linalg.funm aufgerufen werden. Dieser Befehl nimmt die Matrix und eine beliebige Python-Funktion entgegen. Er implementiert dann einen Algorithmus aus dem Buch „Matrix Computations“ von Golub und Van Loan, um die auf die Matrix angewendete Funktion mittels einer Schur-Zerlegung zu berechnen. Beachten Sie, dass *die Funktion komplexe Zahlen als Eingabe akzeptieren muss*, um mit diesem Algorithmus zu funktionieren. Zum Beispiel berechnet der folgende Code die Bessel-Funktion nullter Ordnung, angewendet auf eine Matrix.
>>> from scipy import special, linalg
>>> rng = np.random.default_rng()
>>> A = rng.random((3, 3))
>>> B = linalg.funm(A, lambda x: special.jv(0, x))
>>> A
array([[0.06369197, 0.90647174, 0.98024544],
[0.68752227, 0.5604377 , 0.49142032],
[0.86754578, 0.9746787 , 0.37932682]])
>>> B
array([[ 0.6929219 , -0.29728805, -0.15930896],
[-0.16226043, 0.71967826, -0.22709386],
[-0.19945564, -0.33379957, 0.70259022]])
>>> linalg.eigvals(A)
array([ 1.94835336+0.j, -0.72219681+0.j, -0.22270006+0.j])
>>> special.jv(0, linalg.eigvals(A))
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])
>>> linalg.eigvals(B)
array([0.25375345+0.j, 0.87379738+0.j, 0.98763955+0.j])
Beachten Sie, wie die Bessel-Funktion aufgrund der Definition von Matrix-analytischen Funktionen auf die Eigenwerte der Matrix gewirkt hat.
Spezielle Matrizen#
SciPy und NumPy bieten mehrere Funktionen zur Erstellung spezieller Matrizen, die häufig im Ingenieurwesen und in der Wissenschaft verwendet werden.
Typ |
Funktion |
Beschreibung |
|---|---|---|
Blockdiagonal |
Erstellt eine Blockdiagonalmatrix aus den bereitgestellten Arrays. |
|
circulant |
Erstellt eine zirkulante Matrix. |
|
Begleitmatrix |
Erstellt eine Begleitmatrix. |
|
Faltung |
Erstellt eine Faltungsmatrix. |
|
Diskrete Fourier-Transformation |
Erstellt eine Matrix der diskreten Fourier-Transformation. |
|
Fiedler |
Erstellt eine symmetrische Fiedler-Matrix. |
|
Fiedler Begleitmatrix |
Erstellt eine Fiedler-Begleitmatrix. |
|
Hadamard |
Erstellt eine Hadamard-Matrix. |
|
Hankel |
Erstellt eine Hankel-Matrix. |
|
Helmert |
Erstellt eine Helmert-Matrix. |
|
Hilbert |
Erstellt eine Hilbert-Matrix. |
|
Inverse Hilbert |
Erstellt die Inverse einer Hilbert-Matrix. |
|
Leslie |
Erstellt eine Leslie-Matrix. |
|
Pascal |
Erstellt eine Pascal-Matrix. |
|
Inverse Pascal |
Erstellt die Inverse einer Pascal-Matrix. |
|
Toeplitz |
Erstellt eine Toeplitz-Matrix. |
|
Vandermonde |
Erstellt eine Vandermonde-Matrix. |
Beispiele für die Verwendung dieser Funktionen finden Sie in den jeweiligen Docstrings.
Erweiterte Funktionen#
Batch-Unterstützung#
Einige der linearen Algebra-Funktionen von SciPy können Stapel von Skalaren, 1D- oder 2D-Arrays als N-D-Array-Eingabe verarbeiten. Zum Beispiel kann eine lineare Algebra-Funktion, die typischerweise eine (2D) Matrix akzeptiert, ein Array der Form (4, 3, 2) akzeptieren, das sie als einen Stapel von vier 3x2-Matrizen interpretieren würde. In diesem Fall sagen wir, dass die *Kernform* der Eingabe (3, 2) und die *Stapelform* (4,) ist. Ebenso würde eine lineare Algebra-Funktion, die typischerweise einen (1D) Vektor akzeptiert, ein (4, 3, 2)-Array als einen (4, 3)-Stapel von Vektoren behandeln, in welchem Fall die *Kernform* der Eingabe (2,) und die *Stapelform* (4, 3) ist. Die Länge der Kernform wird auch als *Kerndimension* bezeichnet. In diesen Fällen ist die endgültige Form der Ausgabe die Stapelform der Eingabe, verkettet mit der Kernform der Ausgabe (d. h. die Form der Ausgabe, wenn die Stapelform der Eingabe () ist). Weitere Informationen finden Sie unter Batch-Operationen der Linearen Algebra.