scipy.special.yn#
- scipy.special.yn(n, x, out=None) = <ufunc 'yn'>#
Bessel-Funktion zweiter Art mit ganzzahligem Ordnungswert und reellem Argument.
- Parameter:
- narray_like
Ordnung (ganze Zahl).
- xarray_like
Argument (float).
- outndarray, optional
Optionales Ausgabe-Array für die Funktionsergebnisse
- Rückgabe:
- Yskalar oder ndarray
Wert der Bessel-Funktion, \(Y_n(x)\).
Siehe auch
Hinweise
Wrapper für die Cephes [1] Routine
yn.Die Funktion wird durch Vorwärtsrezirkulation über n ausgewertet, beginnend mit Werten, die von den Cephes-Routinen
y0undy1berechnet wurden. Wennn = 0oder 1 ist, wird die Routine füry0odery1direkt aufgerufen.Referenzen
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
Beispiele
Auswertung der Funktion der Ordnung 0 an einem Punkt.
>>> from scipy.special import yn >>> yn(0, 1.) 0.08825696421567697
Auswertung der Funktion an einem Punkt für verschiedene Ordnungen.
>>> yn(0, 1.), yn(1, 1.), yn(2, 1.) (0.08825696421567697, -0.7812128213002888, -1.6506826068162546)
Die Auswertung für verschiedene Ordnungen kann in einem Aufruf erfolgen, indem eine Liste oder ein NumPy-Array als Argument für den Parameter v übergeben wird.
>>> yn([0, 1, 2], 1.) array([ 0.08825696, -0.78121282, -1.65068261])
Auswertung der Funktion an mehreren Punkten für Ordnung 0 durch Übergabe eines Arrays für z.
>>> import numpy as np >>> points = np.array([0.5, 3., 8.]) >>> yn(0, points) array([-0.44451873, 0.37685001, 0.22352149])
Wenn z ein Array ist, muss der Ordnungs-Parameter v so broadcastfähig sein, dass die korrekte Form entsteht, wenn in einem Aufruf unterschiedliche Ordnungen berechnet werden sollen. Um die Ordnungen 0 und 1 für ein 1D-Array zu berechnen
>>> orders = np.array([[0], [1]]) >>> orders.shape (2, 1)
>>> yn(orders, points) array([[-0.44451873, 0.37685001, 0.22352149], [-1.47147239, 0.32467442, -0.15806046]])
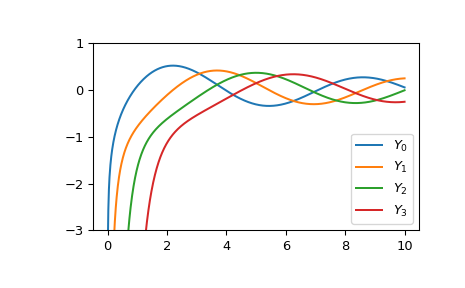
Zeichnen Sie die Funktionen der Ordnungen 0 bis 3 von 0 bis 10.
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> x = np.linspace(0., 10., 1000) >>> for i in range(4): ... ax.plot(x, yn(i, x), label=f'$Y_{i!r}$') >>> ax.set_ylim(-3, 1) >>> ax.legend() >>> plt.show()