scipy.fft.

fft#

scipy.fft.fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *, plan=None)[Quelle]#

Berechnet die 1-D diskrete Fourier-Transformation.

Diese Funktion berechnet die n-Punkte diskrete Fourier-Transformation (DFT) der 1. Dimension mit dem effizienten Fast Fourier Transform (FFT) Algorithmus [1].

Parameter:

xarray_like: Eingabearray, kann komplex sein.
nint, optional: Länge der transformierten Achse der Ausgabe. Wenn n kleiner ist als die Länge der Eingabe, wird die Eingabe gekürzt. Wenn sie größer ist, wird die Eingabe mit Nullen aufgefüllt. Wenn n nicht angegeben ist, wird die Länge der Eingabe entlang der durch axis angegebenen Achse verwendet.
axisint, optional: Achse, entlang derer die FFT berechnet werden soll. Wenn nicht angegeben, wird die letzte Achse verwendet.
norm{“backward”, “ortho”, “forward”}, optional: Normalisierungsmodus. Standard ist „backward“, was bedeutet, dass keine Normalisierung bei den Vorwärtstransformationen und Skalierung mit 1/n bei der ifft erfolgt. „forward“ wendet stattdessen den Faktor 1/n auf die Vorwärtstransformation an. Für norm="ortho" werden beide Richtungen mit 1/sqrt(n) skaliert.

Hinzugefügt in Version 1.6.0: Optionen norm={"forward", "backward"} wurden hinzugefügt
overwrite_xbool, optional: Wenn True, kann der Inhalt von x zerstört werden; der Standardwert ist False. Siehe die Hinweise unten für weitere Details.
workersint, optional: Maximale Anzahl von Workern für parallele Berechnungen. Wenn negativ, wickelt sich der Wert von os.cpu_count() herum. Weitere Details finden Sie unten.
planobject, optional: Dieses Argument ist für die Übergabe eines vorab berechneten Plans von nachgelagerten FFT-Anbietern reserviert. Es wird derzeit in SciPy nicht verwendet.

Hinzugefügt in Version 1.5.0.

Rückgabe:

outcomplex ndarray: Die abgeschnittene oder mit Nullen aufgefüllte Eingabe, transformiert entlang der durch axis angegebenen Achse oder der letzten Achse, wenn axis nicht angegeben ist.

Löst aus:

IndexError: wenn achsen größer ist als die letzte Achse von x.

Siehe auch

ifft: Die Inverse von fft.
fft2: Die 2-D FFT.
fftn: Die N-dimensionale FFT.
rfftn: Die N-D FFT für reale Eingaben.
fftfreq: Frequenzbänder für gegebene FFT-Parameter.
next_fast_len: Größe, auf die die Eingabe für die effizientesten Transformationen aufgefüllt wird

Hinweise

FFT (Fast Fourier Transform) bezieht sich auf eine Methode, mit der die diskrete Fourier-Transformation (DFT) effizient berechnet werden kann, indem Symmetrien in den berechneten Termen genutzt werden. Die Symmetrie ist am höchsten, wenn n eine Zweierpotenz ist, und die Transformation ist daher für solche Größen am effizientesten. Für schlecht zerlegbare Größen verwendet scipy.fft den Algorithmus von Bluestein [2] und ist daher nie schlechter als O(n log n). Weitere Leistungsverbesserungen können durch Auffüllen der Eingabe mit Nullen mit next_fast_len erzielt werden.

Wenn x ein 1D-Array ist, dann ist die fft äquivalent zu

y[k] = np.sum(x * np.exp(-2j * np.pi * k * np.arange(n)/n))

Der Frequenzterm f=k/n befindet sich bei y[k]. Bei y[n/2] erreichen wir die Nyquist-Frequenz und gehen zu den Negativfrequenztermen über. Bei einer 8-Punkte-Transformation sind die Frequenzen des Ergebnisses also [0, 1, 2, 3, -4, -3, -2, -1]. Um die FFT-Ausgabe so anzuordnen, dass die Nullfrequenzkomponente zentriert ist, wie [-4, -3, -2, -1, 0, 1, 2, 3], verwenden Sie fftshift.

Transformationen können in einfacher, doppelter oder erweiterter Präzision (long double) Gleitkommazahlen durchgeführt werden. Eingaben in halber Präzision werden in einfache Präzision umgewandelt und nicht-Gleitkommazahl-Eingaben werden in doppelte Präzision umgewandelt.

Wenn der Datentyp von x reell ist, wird automatisch ein „Real FFT“-Algorithmus verwendet, der die Berechnungszeit etwa halbiert. Um die Effizienz noch etwas weiter zu steigern, verwenden Sie rfft, das die gleiche Berechnung durchführt, aber nur die Hälfte des symmetrischen Spektrums ausgibt. Wenn die Daten sowohl reell als auch symmetrisch sind, kann die dct die Effizienz erneut verdoppeln, indem die Hälfte des Spektrums aus der Hälfte des Signals generiert wird.

Wenn overwrite_x=True angegeben ist, kann der von x referenzierte Speicher von der Implementierung beliebig verwendet werden. Dies kann die Wiederverwendung des Speichers für das Ergebnis beinhalten, ist aber keinesfalls garantiert. Sie sollten sich nach der Transformation nicht auf den Inhalt von x verlassen, da sich dieser ohne Vorwarnung in Zukunft ändern kann.

Das Argument workers gibt die maximale Anzahl paralleler Jobs an, in die die FFT-Berechnung aufgeteilt wird. Dies führt unabhängige 1-D-FFTs innerhalb von x aus. Daher muss x mindestens 2-dimensional sein und die nicht-transformierten Achsen müssen groß genug sein, um sie in Chunks aufzuteilen. Wenn x zu klein ist, können weniger Jobs als angefordert verwendet werden.

Referenzen

[1]

Cooley, James W., und John W. Tukey, 1965, „An algorithm for the machine calculation of complex Fourier series“, Math. Comput. 19: 297-301.

[2]

Bluestein, L., 1970, „A linear filtering approach to the computation of discrete Fourier transform“. IEEE Transactions on Audio and Electroacoustics. 18 (4): 451-455.

Beispiele

>>> import scipy.fft
>>> import numpy as np
>>> scipy.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-2.33486982e-16+1.14423775e-17j,  8.00000000e+00-1.25557246e-15j,
        2.33486982e-16+2.33486982e-16j,  0.00000000e+00+1.22464680e-16j,
       -1.14423775e-17+2.33486982e-16j,  0.00000000e+00+5.20784380e-16j,
        1.14423775e-17+1.14423775e-17j,  0.00000000e+00+1.22464680e-16j])

In diesem Beispiel hat eine reelle Eingabe eine FFT, die hermitesch ist, d. h. im Realteil symmetrisch und im Imaginärteil antisymmetrisch.

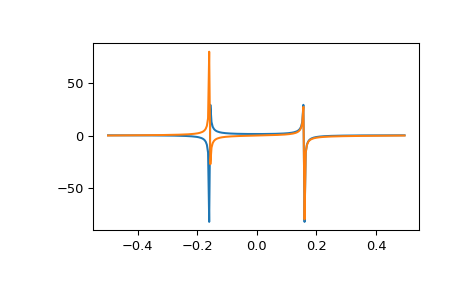
>>> from scipy.fft import fft, fftfreq, fftshift
>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
>>> sp = fftshift(fft(np.sin(t)))
>>> freq = fftshift(fftfreq(t.shape[-1]))
>>> plt.plot(freq, sp.real, freq, sp.imag)
[<matplotlib.lines.Line2D object at 0x...>,
 <matplotlib.lines.Line2D object at 0x...>]
>>> plt.show()