scipy.fft.

fftn

scipy.fft.fftn(x, s=None, axes=None, norm=None, overwrite_x=False, workers=None, *, plan=None)

Berechnet die N-D diskrete Fourier-Transformation.

Diese Funktion berechnet die N-D diskrete Fourier-Transformation über eine beliebige Anzahl von Achsen eines M-D-Arrays mittels der Fast Fourier Transform (FFT).

Parameter:

xarray_like

Eingabearray, kann komplex sein.

sSequenz von ganzen Zahlen, optional

Form (Länge jeder transformierten Achse) der Ausgabe (s[0] bezieht sich auf Achse 0, s[1] auf Achse 1, usw.). Dies entspricht n für fft(x, n). Entlang einer Achse wird die Eingabe abgeschnitten, wenn die angegebene Form kleiner ist als die der Eingabe. Wenn sie größer ist, wird die Eingabe mit Nullen aufgefüllt. Wenn s nicht angegeben ist, wird die Form der Eingabe entlang der durch axes angegebenen Achsen verwendet.

axesSequenz von ganzen Zahlen, optional

Achsen, über die die FFT berechnet werden soll. Wenn nicht angegeben, werden die letzten len(s) Achsen verwendet, oder alle Achsen, wenn auch s nicht angegeben ist.

norm{“backward”, “ortho”, “forward”}, optional

Normalisierungsmodus (siehe fft). Standard ist „backward“.

overwrite_xbool, optional

Wenn True, kann der Inhalt von x zerstört werden; Standard ist False. Weitere Einzelheiten finden Sie unter fft.

workersint, optional

Maximale Anzahl von Workern, die für die parallele Berechnung verwendet werden sollen. Wenn negativ, wickelt sich der Wert von os.cpu_count() ab. Weitere Einzelheiten finden Sie unter fft.

planobject, optional

Dieses Argument ist für die Übergabe eines vorab berechneten Plans von nachgelagerten FFT-Anbietern reserviert. Es wird derzeit in SciPy nicht verwendet.

Hinzugefügt in Version 1.5.0.

Rückgabe:

outcomplex ndarray

Die trunkierte oder mit Nullen aufgefüllte Eingabe, transformiert entlang der Achsen, die durch axes angegeben sind, oder durch eine Kombination aus s und x, wie im Abschnitt Parameter oben erläutert.

Löst aus:

ValueError

Wenn s und axes unterschiedliche Längen haben.

IndexError

Wenn ein Element von axes größer ist als die Anzahl der Achsen von x.

Siehe auch

ifftn

Die Umkehrung von fftn, die inverse N-D FFT.

fft

Die 1-D FFT mit Definitionen und Konventionen.

rfftn

Die N-D FFT für reale Eingaben.

fft2

Die 2-D FFT.

fftshift

Verschiebt Frequenzen bei Null zur Mitte des Arrays.

Hinweise

Die Ausgabe enthält, analog zu fft, den Term für die Frequenz Null in der Ecke niedriger Ordnungen aller Achsen, die positiven Frequenzterme in der ersten Hälfte aller Achsen, den Term für die Nyquist-Frequenz in der Mitte aller Achsen und die negativen Frequenzterme in der zweiten Hälfte aller Achsen, geordnet nach abnehmend negativer Frequenz.

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import scipy.fft
>>> import numpy as np
>>> x = np.mgrid[:3, :3, :3][0]
>>> scipy.fft.fftn(x, axes=(1, 2))
array([[[ 0.+0.j,   0.+0.j,   0.+0.j], # may vary
        [ 0.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j]],
       [[ 9.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j]],
       [[18.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j]]])
>>> scipy.fft.fftn(x, (2, 2), axes=(0, 1))
array([[[ 2.+0.j,  2.+0.j,  2.+0.j], # may vary
        [ 0.+0.j,  0.+0.j,  0.+0.j]],
       [[-2.+0.j, -2.+0.j, -2.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j]]])

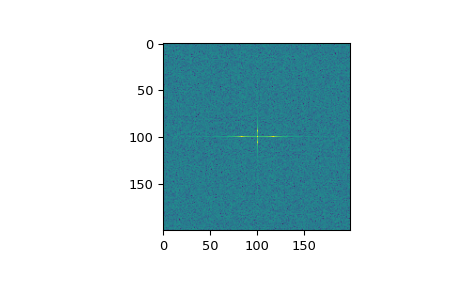
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> [X, Y] = np.meshgrid(2 * np.pi * np.arange(200) / 12,
...                      2 * np.pi * np.arange(200) / 34)
>>> S = np.sin(X) + np.cos(Y) + rng.uniform(0, 1, X.shape)
>>> FS = scipy.fft.fftn(S)
>>> plt.imshow(np.log(np.abs(scipy.fft.fftshift(FS))**2))
<matplotlib.image.AxesImage object at 0x...>
>>> plt.show()

ZurückIn Tab öffnen