fht#
- scipy.fft.fht(a, dln, mu, offset=0.0, bias=0.0)[Quelle]#
Berechnet die schnelle Hankel-Transformation.
Berechnet die diskrete Hankel-Transformation einer logarithmisch gleichmäßig verteilten periodischen Sequenz unter Verwendung des FFTLog-Algorithmus [1], [2].
- Parameter:
- aarray_like (…, n)
Reelle periodische Eingabearray, gleichmäßig logarithmisch verteilt. Für mehrdimensionale Eingaben wird die Transformation über die letzte Achse durchgeführt.
- dlnfloat
Gleichmäßige logarithmische Verteilung des Eingabearrays.
- mufloat
Ordnung der Hankel-Transformation, eine beliebige positive oder negative reelle Zahl.
- offsetfloat, optional
Offset der gleichmäßigen logarithmischen Verteilung des Ausgabe-Arrays.
- biasfloat, optional
Exponent des Potenzgesetz-Bias, eine beliebige positive oder negative reelle Zahl.
- Rückgabe:
- Aarray_like (…, n)
Das transformierte Ausgabe-Array, das reell, periodisch, gleichmäßig logarithmisch verteilt und von der gleichen Form wie das Eingabe-Array ist.
Hinweise
Diese Funktion berechnet eine diskrete Version der Hankel-Transformation
\[A(k) = \int_{0}^{\infty} \! a(r) \, J_\mu(kr) \, k \, dr \;,\]wobei \(J_\mu\) die Bessel-Funktion der Ordnung \(\mu\) ist. Der Index \(\mu\) kann jede reelle Zahl sein, positiv oder negativ. Beachten Sie, dass die numerische Hankel-Transformation einen Integranden von \(k \, dr\) verwendet, während die mathematische Hankel-Transformation üblicherweise mit \(r \, dr\) definiert ist.
Das Eingabe-Array a ist eine periodische Sequenz der Länge \(n\), die gleichmäßig logarithmisch mit dem Abstand dln verteilt ist,
\[a_j = a(r_j) \;, \quad r_j = r_c \exp[(j-j_c) \, \mathtt{dln}]\]zentriert um den Punkt \(r_c\). Beachten Sie, dass der zentrale Index \(j_c = (n-1)/2\) halb-ganzzahlig ist, wenn \(n\) gerade ist, so dass \(r_c\) zwischen zwei Eingabeelementen liegt. Ebenso ist das Ausgabe-Array A eine periodische Sequenz der Länge \(n\), ebenfalls gleichmäßig logarithmisch verteilt mit dem Abstand dln
\[A_j = A(k_j) \;, \quad k_j = k_c \exp[(j-j_c) \, \mathtt{dln}]\]zentriert um den Punkt \(k_c\).
Die Mittelpunkte \(r_c\) und \(k_c\) der periodischen Intervalle können beliebig gewählt werden, aber es ist üblich, das Produkt \(k_c r_c = k_j r_{n-1-j} = k_{n-1-j} r_j\) gleich eins zu setzen. Dies kann über den Parameter offset geändert werden, der den logarithmischen Offset \(\log(k_c) = \mathtt{offset} - \log(r_c)\) des Ausgabe-Arrays steuert. Die Wahl eines optimalen Werts für offset kann das Klingeln der diskreten Hankel-Transformation reduzieren.
Wenn der Parameter bias ungleich Null ist, berechnet diese Funktion eine diskrete Version der verzerrten Hankel-Transformation
\[A(k) = \int_{0}^{\infty} \! a_q(r) \, (kr)^q \, J_\mu(kr) \, k \, dr\]wobei \(q\) der Wert von bias ist und eine Potenzgesetz-Verzerrung \((kr)^q\) auf die Eingabesequenz angewendet wird, d. h. \(a_q(r) = a(r) \, (kr)^{-q}\). Das Verzerren der Transformation kann helfen, die kontinuierliche Transformation von \(a(r)\) anzunähern, wenn es einen Wert \(q\) gibt, so dass \(a_q(r)\) nahe an einer periodischen Sequenz liegt. In diesem Fall wird die resultierende \(A(k)\) nahe an der kontinuierlichen Transformation liegen.
Referenzen
[1]Talman J. D., 1978, J. Comp. Phys., 29, 35
Beispiele
Dieses Beispiel ist die angepasste Version von
fftlogtest.f, die in [2] enthalten ist. Es wertet das Integral aus\[\int^\infty_0 r^{\mu+1} \exp(-r^2/2) J_\mu(kr) k dr = k^{\mu+1} \exp(-k^2/2) .\]>>> import numpy as np >>> from scipy import fft >>> import matplotlib.pyplot as plt
Parameter für die Transformation.
>>> mu = 0.0 # Order mu of Bessel function >>> r = np.logspace(-7, 1, 128) # Input evaluation points >>> dln = np.log(r[1]/r[0]) # Step size >>> offset = fft.fhtoffset(dln, initial=-6*np.log(10), mu=mu) >>> k = np.exp(offset)/r[::-1] # Output evaluation points
Definiere die analytische Funktion.
>>> def f(x, mu): ... """Analytical function: x^(mu+1) exp(-x^2/2).""" ... return x**(mu + 1)*np.exp(-x**2/2)
Werte die Funktion an
raus und berechne die entsprechenden Werte ankmit FFTLog.>>> a_r = f(r, mu) >>> fht = fft.fht(a_r, dln, mu=mu, offset=offset)
Für dieses Beispiel können wir tatsächlich die analytische Antwort (die in diesem Fall mit der Eingabefunktion identisch ist) zum Vergleich berechnen und den relativen Fehler ermitteln.
>>> a_k = f(k, mu) >>> rel_err = abs((fht-a_k)/a_k)
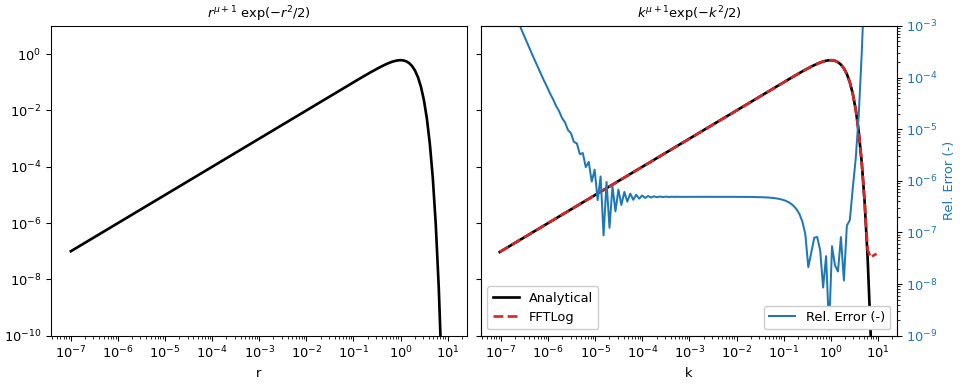
Plotte das Ergebnis.
>>> figargs = {'sharex': True, 'sharey': True, 'constrained_layout': True} >>> fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4), **figargs) >>> ax1.set_title(r'$r^{\mu+1}\ \exp(-r^2/2)$') >>> ax1.loglog(r, a_r, 'k', lw=2) >>> ax1.set_xlabel('r') >>> ax2.set_title(r'$k^{\mu+1} \exp(-k^2/2)$') >>> ax2.loglog(k, a_k, 'k', lw=2, label='Analytical') >>> ax2.loglog(k, fht, 'C3--', lw=2, label='FFTLog') >>> ax2.set_xlabel('k') >>> ax2.legend(loc=3, framealpha=1) >>> ax2.set_ylim([1e-10, 1e1]) >>> ax2b = ax2.twinx() >>> ax2b.loglog(k, rel_err, 'C0', label='Rel. Error (-)') >>> ax2b.set_ylabel('Rel. Error (-)', color='C0') >>> ax2b.tick_params(axis='y', labelcolor='C0') >>> ax2b.legend(loc=4, framealpha=1) >>> ax2b.set_ylim([1e-9, 1e-3]) >>> plt.show()