scipy.interpolate.

BarycentricInterpolator#

class scipy.interpolate.BarycentricInterpolator(xi, yi=None, axis=0, *, wi=None, rng=None)[Quelle]#

Baryzentrischer (Lagrange mit verbesserter Stabilität) Interpolator (C∞ glatt).

Konstruiert ein Polynom, das durch eine gegebene Menge von Punkten verläuft. Ermöglicht die Auswertung des Polynoms und all seiner Ableitungen, effizientes Ändern der zu interpolierenden y-Werte und Aktualisierung durch Hinzufügen weiterer x- und y-Werte. Zur numerischen Stabilität wird eine baryzentrische Darstellung verwendet, anstatt die Koeffizienten des Polynoms direkt zu berechnen.

Parameter:

xiarray_like, shape (npoints, )

1-D-Array der x-Koordinaten der Punkte, die das Polynom durchlaufen soll

yiarray_like, shape (…, npoints, …), optional

N-D-Array der y-Koordinaten der Punkte, die das Polynom durchlaufen soll. Wenn None, werden die y-Werte später über die Methode set_y bereitgestellt. Die Länge von yi entlang der Interpolationsachse muss gleich der Länge von xi sein. Verwenden Sie den Parameter axis, um die richtige Achse auszuwählen.

axisint, optional

Achse im yi-Array, die den x-Koordinatenwerten entspricht. Standardmäßig axis=0.

wiarray_like, optional

Die baryzentrischen Gewichte für die ausgewählten Interpolationspunkte xi. Wenn abwesend oder None, werden die Gewichte aus xi berechnet (Standard). Dies ermöglicht die Wiederverwendung der Gewichte wi, wenn mehrere Interpolatoren mit denselben Knoten xi berechnet werden, ohne Neukalkulation. Dies ermöglicht auch die explizite Berechnung der Gewichte für einige Wahlmöglichkeiten von xi (siehe Hinweise).

rng{None, int, numpy.random.Generator}, optional

Wenn rng als Schlüsselwort übergeben wird, werden andere Typen als numpy.random.Generator an numpy.random.default_rng übergeben, um einen Generator zu instanziieren. Wenn rng bereits eine Generator-Instanz ist, wird die bereitgestellte Instanz verwendet. Geben Sie rng für reproduzierbare Interpolation an.

Wenn dieses Argument random_state als Schlüsselwort übergeben wird, gilt das Legacy-Verhalten für das Argument random_state

Wenn random_state None ist (oder numpy.random), wird die Singleton-Instanz numpy.random.RandomState verwendet.
Wenn random_state eine Ganzzahl ist, wird eine neue RandomState-Instanz verwendet, die mit random_state initialisiert wurde.
Wenn random_state bereits eine Generator- oder RandomState-Instanz ist, wird diese Instanz verwendet.

Geändert in Version 1.15.0: Als Teil des SPEC-007-Übergangs von der Verwendung von numpy.random.RandomState zu numpy.random.Generator wurde dieses Schlüsselwort von random_state zu rng geändert. Für eine Übergangszeit funktionieren beide Schlüsselwörter weiterhin (geben Sie nur eines davon an). Nach der Übergangszeit gibt die Verwendung des Schlüsselworts random_state Warnungen aus. Das Verhalten der Schlüsselwörter random_state und rng ist oben beschrieben.

Attribute:

dtype

Methoden

`__call__`(x)	Wertet das interpolierende Polynom an den Punkten x aus
`add_xi`(xi[, yi])	Fügt dem zu interpolierenden Satz weitere x-Werte hinzu
`derivative`(x[, der])	Wertet eine einzelne Ableitung des Polynoms am Punkt x aus.
`derivatives`(x[, der])	Mehrere Ableitungen des Polynoms an der Stelle x auswerten
`set_yi`(yi[, axis])	Aktualisiert die zu interpolierenden y-Werte

Hinweise

Diese Methode ist eine Variante der Lagrange-Polynominterpolation [1], basierend auf [2]. Anstatt die Lagrange- oder Newton-Formel zu verwenden, wird das Polynom durch die baryzentrische Formel dargestellt

\[p(x) = \frac{\sum_{i=1}^m\ w_i y_i / (x - x_i)}{\sum_{i=1}^m w_i / (x - x_i)},\]

wobei \(w_i\) die baryzentrischen Gewichte sind, die mit der allgemeinen Formel berechnet werden

\[w_i = \left( \prod_{k \neq i} x_i - x_k \right)^{-1}.\]

Dies ist die gleiche baryzentrische Form, die von AAA und FloaterHormannInterpolator verwendet wird. Im Gegensatz dazu sind die Gewichte \(w_i\) so definiert, dass \(p(x)\) ein Polynom und keine rationale Funktion ist.

Die baryzentrische Darstellung vermeidet viele der Probleme, die bei der Polynominterpolation durch Gleitkommaarithmetik auftreten. Sie vermeidet jedoch keine Probleme, die der Polynominterpolation inhärent sind. Nämlich, wenn die x-Koordinaten gleichmäßig verteilt sind, dann können die Gewichte explizit mit der Formel aus [2] berechnet werden

\[w_i = (-1)^i {n \choose i},\]

wobei \(n\) die Anzahl der x-Koordinaten ist. Wie in [2] angemerkt, bedeutet dies, dass für große \(n\) die Gewichte um exponentiell große Faktoren variieren, was zum Runge-Phänomen führt.

Um diese schlechte Konditionierung zu vermeiden, sollten die x-Koordinaten an den Endpunkten des Intervalls gehäuft sein. Eine ausgezeichnete Wahl von Punkten im Intervall \([a,b]\) sind Chebyshev-Punkte der zweiten Art

\[x_i = \frac{a + b}{2} + \frac{a - b}{2}\cos(i\pi/n).\]

in welchem Fall die Gewichte explizit wie folgt berechnet werden können

\[\begin{split}w_i = \begin{cases} (-1)^i/2 & i = 0,n \\ (-1)^i & \text{sonst} \end{cases}.\end{split}\]

Weitere Informationen finden Sie in [2]. Beachten Sie, dass für große \(n\) die explizite Berechnung der Gewichte (siehe Beispiele) schneller ist als die allgemeine Formel.

Referenzen

[1]

https://en.wikipedia.org/wiki/Lagrange_polynomial

[2] (1,2,3,4)

Jean-Paul Berrut und Lloyd N. Trefethen, „Barycentric Lagrange Interpolation“, SIAM Review 2004 46:3, 501-517 DOI:10.1137/S0036144502417715

Beispiele

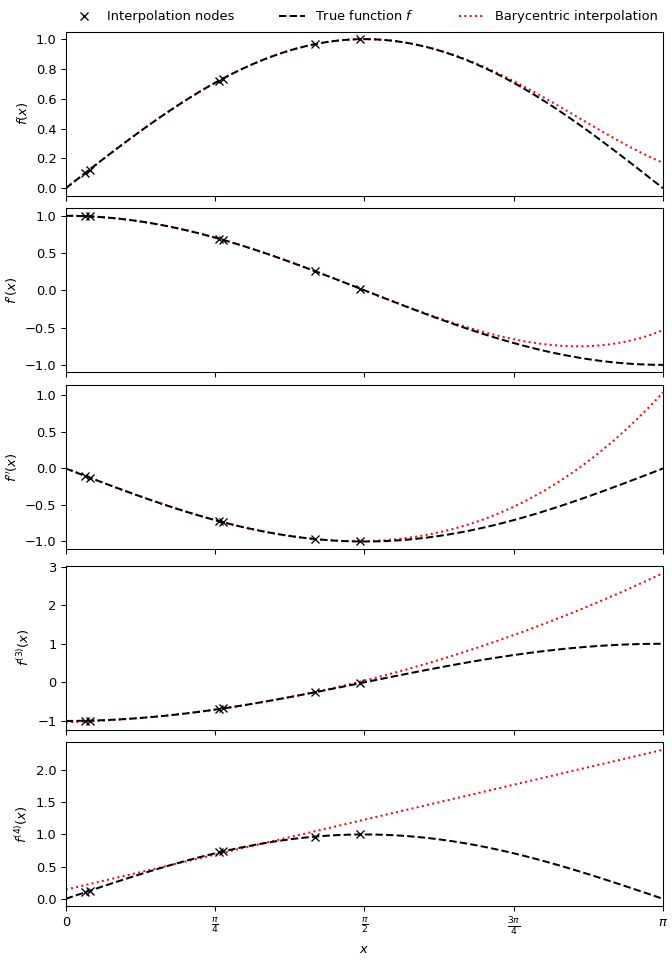
Zur Erzeugung eines quintischen baryzentrischen Interpolanten, der die Funktion \(\sin x\) und ihre ersten vier Ableitungen annähert, unter Verwendung von sechs zufällig verteilten Knoten in \((0, \pi/2)\)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import BarycentricInterpolator
>>> rng = np.random.default_rng()
>>> xi = rng.random(6) * np.pi/2
>>> f, f_d1, f_d2, f_d3, f_d4 = np.sin, np.cos, lambda x: -np.sin(x), lambda x: -np.cos(x), np.sin
>>> P = BarycentricInterpolator(xi, f(xi), random_state=rng)
>>> fig, axs = plt.subplots(5, 1, sharex=True, layout='constrained', figsize=(7,10))
>>> x = np.linspace(0, np.pi, 100)
>>> axs[0].plot(x, P(x), 'r:', x, f(x), 'k--', xi, f(xi), 'xk')
>>> axs[1].plot(x, P.derivative(x), 'r:', x, f_d1(x), 'k--', xi, f_d1(xi), 'xk')
>>> axs[2].plot(x, P.derivative(x, 2), 'r:', x, f_d2(x), 'k--', xi, f_d2(xi), 'xk')
>>> axs[3].plot(x, P.derivative(x, 3), 'r:', x, f_d3(x), 'k--', xi, f_d3(xi), 'xk')
>>> axs[4].plot(x, P.derivative(x, 4), 'r:', x, f_d4(x), 'k--', xi, f_d4(xi), 'xk')
>>> axs[0].set_xlim(0, np.pi)
>>> axs[4].set_xlabel(r"$x$")
>>> axs[4].set_xticks([i * np.pi / 4 for i in range(5)],
...                   ["0", r"$\frac{\pi}{4}$", r"$\frac{\pi}{2}$", r"$\frac{3\pi}{4}$", r"$\pi$"])
>>> for ax, label in zip(axs, ("$f(x)$", "$f'(x)$", "$f''(x)$", "$f^{(3)}(x)$", "$f^{(4)}(x)$")):
...     ax.set_ylabel(label)
>>> labels = ['Interpolation nodes', 'True function $f$', 'Barycentric interpolation']
>>> axs[0].legend(axs[0].get_lines()[::-1], labels, bbox_to_anchor=(0., 1.02, 1., .102),
...               loc='lower left', ncols=3, mode="expand", borderaxespad=0., frameon=False)
>>> plt.show()

../../_images/scipy-interpolate-BarycentricInterpolator-1_00_00.png

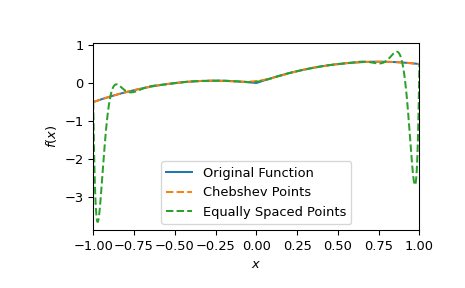
Als Nächstes zeigen wir, wie die Verwendung von Chebyshev-Punkten der zweiten Art die Vermeidung des Runge-Phänomens ermöglicht. In diesem Beispiel berechnen wir auch die Gewichte explizit.

>>> n = 20
>>> def f(x): return np.abs(x) + 0.5*x - x**2
>>> i = np.arange(n)
>>> x_cheb = np.cos(i*np.pi/(n - 1))  # Chebyshev points on [-1, 1]
>>> w_i_cheb = (-1.)**i  # Explicit formula for weights of Chebyshev points
>>> w_i_cheb[[0, -1]] /= 2
>>> p_cheb = BarycentricInterpolator(x_cheb, f(x_cheb), wi=w_i_cheb)
>>> x_equi = np.linspace(-1, 1, n)
>>> p_equi = BarycentricInterpolator(x_equi, f(x_equi))
>>> xx = np.linspace(-1, 1, 1000)
>>> fig, ax = plt.subplots()
>>> ax.plot(xx, f(xx), label="Original Function")
>>> ax.plot(xx, p_cheb(xx), "--", label="Chebshev Points")
>>> ax.plot(xx, p_equi(xx), "--", label="Equally Spaced Points")
>>> ax.set(xlabel="$x$", ylabel="$f(x)$", xlim=[-1, 1])
>>> ax.legend()
>>> plt.show()

../../_images/scipy-interpolate-BarycentricInterpolator-1_01_00.png